安徽省池州市第一中学2019-2020学年高一下学期期中教学质量检测数学（文）试题 7页

‎2019～2020学年度第二学期期中教学质量检测 高一数学（文科）试卷 满分：150分 考试时间：120分钟 一、选择题（60分）‎ ‎1．已知全集集合,，下图中阴影部分所表示的集合为( )‎ A． B． ‎ C． D． ‎ ‎2．若，下列不等式一定成立的是（　　）‎ A． B． C． D．‎ ‎3．在有一定规律的数列0，3，8，15，24，x，48，63，…… 中，x的值是（ ）．‎ A．30 B．35 C．36 D．42‎ ‎4．不等式组表示的平面区域是（ ）‎ A ． B． C． D． ‎ ‎5．在△ABC中，给出下列关系式：‎ ‎ ① ② ③‎ 其中正确的个数是 A．0 B．1 C．2 D．3‎ ‎6．记等差数列{an}的前n项和为Sn．若，则（ ）‎ A．7 B．8 C．9 D．10‎ ‎7．已知满足对，，且时，，‎ ‎ 则的值为 A．－1 B．0 C．1 D．2‎ ‎8．在△ABC中，已知三个内角为A，B，C满足：：：5：4，则（ ）‎ A． B． C． D．‎ ‎9．在△ABC中，a、b、c分别是角A、B、C的对边，且满足，那么△ABC的形状一定是（ ）‎ A．等腰三角形 B．直角三角形 C．等腰或直角三角形 D． 等腰直角三角形 ‎10．若x、y满足约束条件，则的最小值是（ ）‎ A．－3 B．0 C． D．3‎ ‎11．已知数列{an}的前n项和为Sn，若，则（ ）‎ A． B． C． D． ‎ ‎12．如图，有一辆汽车在一条水平的公路上向正西行驶，汽车在A点测得公路北侧山顶D的仰角为30°，汽车行驶300m后到达B点测得山顶D在北偏 ‎ 西30°方向上，且仰角为45°，则山的高度CD为（ ）‎ A． B． ‎ C． D．300m ‎ 二、填空题（20分）‎ ‎13．已知，则__________．‎ ‎14．已知三角形ABC的三边长分别为a,b,c，若6、a、b、c、2成等差数列，则该三角形的面积为 ． ‎ ‎15．若数列{an}为等差数列，{bn}为等比数列，且满足：，，函数，则 ． ‎ ‎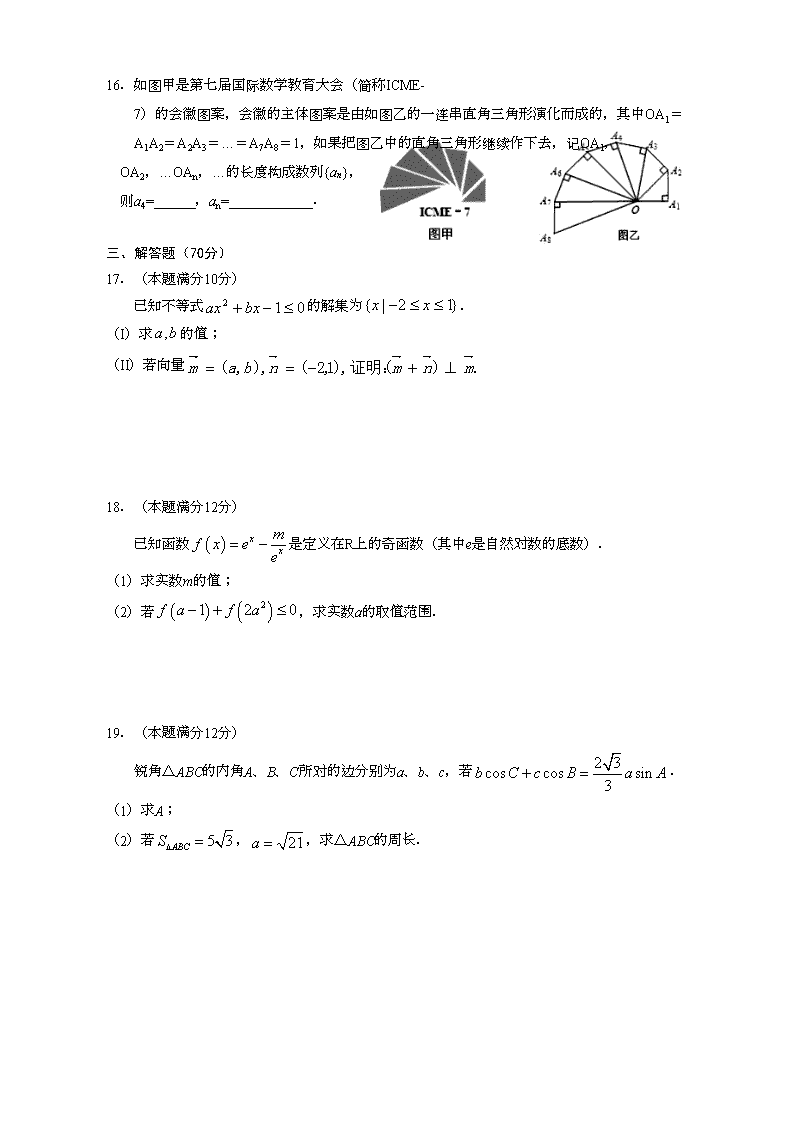16．如图甲是第七届国际数学教育大会（简称ICME-7）的会徽图案，会徽的主体图案是由如图乙的一连串直角三角形演化而成的，其中OA1＝A1A2＝A2A3＝…＝A7A8＝1，如果把图乙中的直角三角形继续作下去，记OA1，‎ ‎ OA2，…OAn，…的长度构成数列{an}，‎ ‎ 则a4=______，an=____________．‎ 三、解答题（70分）‎ ‎17．（本题满分10分）‎ 已知不等式的解集为．‎ ‎（I）求的值；‎ ‎（II）若向量 ‎18．（本题满分12分）‎ 已知函数是定义在R上的奇函数（其中e是自然对数的底数）．‎ ‎（1）求实数m的值；‎ ‎（2）若，求实数a的取值范围． ‎ ‎19．（本题满分12分）‎ 锐角△ABC的内角A、B、C所对的边分别为a、b、c，若．‎ ‎（1）求A；‎ ‎（2）若，，求△ABC的周长．‎ ‎20．（本题满分12分）‎ 已知等比数列{an}为递增数列，，，数列{bn}满足．‎ ‎（1）求数列{bn}的通项公式；‎ ‎（2）求数列的前n项和Sn．‎ ‎21．（本题满分12分）‎ 在等差数列{an}中，=3，其前n项和为Sn，等比数列{bn}的各项均为正数，=1，公比为q,且b2+ S2=12，．‎ ‎（1）求an与bn的通项公式；‎ ‎（2）设数列{ cn }满足，求{ cn }的前n项和Tn．‎ ‎22．（本题满分12分）‎ 如图，在平面四边形ABCD中，，，的面积为．‎ ‎（1）求AC的长；‎ A B D C ‎（2）若AB⊥AD，∠ACB＝θ（θ∈[30°，90°]），当△ABC的面积最大时，求BD的长。‎ ‎2019-2020学年度第二学期期中考试 高一文科数学试题参考答案 一、 选择题：‎ ‎1-12 ADBB CBCB CAAD 二、填空题：‎ ‎13, 18; 14, 6; 15, 16, （第一空2分，第2空3分）‎ 三、解答题 ‎17.（Ⅰ）依题意知的根为1和-2，‎ 由韦达定理得 ------------5分 (2) ‎.................................................................10分 ‎18.解：（1）是定义在R的奇函数， ，‎ 当m=1时，， ......................................6分 ‎（2）∵函数为奇函数，所以................................8分 又因为，易证f(x)是单调递增，.........................................................10分 ‎...........................................................12分 ‎19.（1）由正弦定理，得，有，‎ 从而，解得，‎ 为锐角，因此，；...........................................................................6分 ‎（2），故，....................................................8分 由余弦定理，即，‎ ‎，，‎ 故的周长为．..........................................................12分 ‎20.（1）∵是等比数列∴‎ 又∵,由是递增数列解得，,且公比 ‎∴, ..................................................6分 ‎（2）‎ ‎，两式相减得：‎ ‎∴.......................................................................................12分 ‎21.（1） 设：{}的公差为,‎ 因为.解得=3或=-4（舍）,=3．‎ 故，...............................................6分 ‎（2）因为……………8分 ‎.............................12分 ‎22.⑴∵，，的面积为 ‎∴,‎ ‎∴ ......................................................................................3分 ‎∴由余弦定理得 ‎∴ .............................................................................6分 ‎⑵由（1）知中，，,∴‎ ‎∵,∴ ..................................................8分 ‎.........................9分 ‎................................................................................................................12分 ‎.....................................12分