高中数学选修2-2公开课课件1_4 生活中的优化问题举例 35页

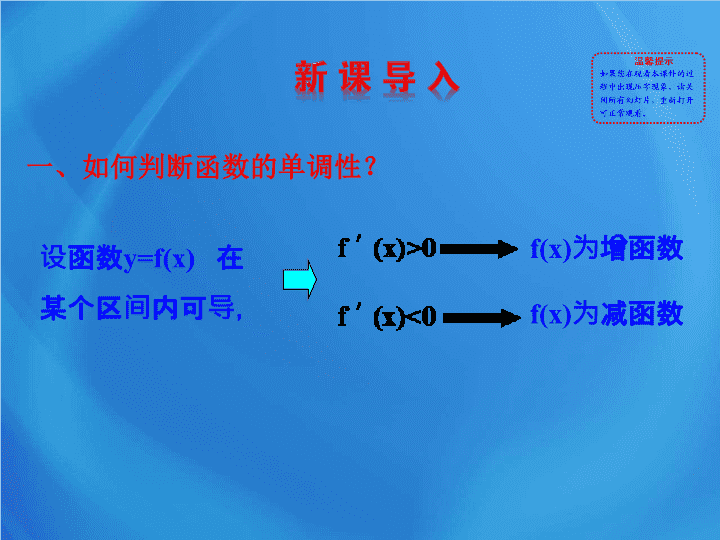
1.4 生活中的优化问题举例 一、如何判断函数的单调性？ f(x) 为增函数 f(x) 为减函数 设函数 y=f(x) 在 某个区间内可导， 二、如何求函数的极值与最值？ 求函数极值的 一般步骤 （ 1 ）确定定义域 （ 2 ）求导数 f′(x) （ 3 ）求 f′(x)=0 的根 （ 4 ）列表（ 5 ）判断 求 f ( x ) 在闭区间 [ a , b ] 上的最值的步骤 (1) 求 f ( x ) 在区间 ( a , b ) 内极值； (2) 将 y = f ( x ) 的各极值与 f ( a ) 、 f ( b ）比较 , 从而确定函数的最值 生活中经常遇到求 利润最大 、 用料最省 、 效率最高 等问题，这些问题通常称为 优化问题 ，通过前面的学习，我们知道，导数是求函数最大（小）值的有力工具，本节我们运用导数，解决一些生活中的优化问题 . 1. 了解导数在实际问题中的应用； 2. 对给出的实际问题，如使利润最大、效率最高、用料最省等问题，体会导数在解决实际问题中的作用； 3. 利用导数知识解决实际中的最优化问题； （重点） 4. 将实际问题转化为数学问题，建立函数模型 . （难点） 探究点 1 海报版面尺寸的设计 例 1 学校或班级举行活动，通常需要张贴海报进行宣传 . 现让你设计一张如图 3.4-1 所示的竖向张贴的海报，要求版心面积为 128dm 2 ，上、下两边各空 2dm ，左、右两边各空 1dm ，如何设计海报的尺寸，才能使四周空白面积最小？ 图 3.4-1 分析：已知版心的面积，你能否设计出版心的高，求出版心的宽，从而列出海报四周的面积来？ 因此， x=16 是函数 S(x) 的极小值点，也是最小值点 . 所以，当版心高为 16dm ，宽为 8dm 时，能使四周空白面积最小 . 你还有其他解法吗？例如用基本不等式行吗？ 解法二： 由解法 ( 一 ) 得 2. 在实际应用题目中，若函数 f ( x ) 在定义域内 只有一个极值点 x 0 ， 则不需与端点比较， f ( x 0 ) 即是所求的最大值或最小值 . 总结提升 1. 设出变量找出函数关系式； 确定出定义域； 所得结果符合问题的实际意义 . ( 所说的区间也适用于开区间或无穷区间 ) 规格（ L ） 0.6 1.25 2 价格（元） 2.5 4.5 5.1 探究点 2 饮料瓶大小对饮料公司利润的影响 例 2 下面是某品牌饮料的三种规格不同的产品，若它们的价格如下表所示，则 （ 1 ）对消费者而言，选择哪一种更合算呢？ （ 2 ）对制造商而言，哪一种的利润更大？ 某制造商制造并出售球形瓶装的某种饮料，瓶子的制造成本是 0.8 p r 2 分，其中 r 是瓶子的半径 ( 单位 :cm) ，已知每出售 1mL 的饮料，制造商可获利 0.2 分，且制造商能制作的瓶子的最大半径为 6cm ， 问题： ( １ ) 瓶子半径多大时，能使每瓶饮料的利润最大？ ( ２）瓶子半径多大时，每瓶饮料的利润最小？ 解： 由于瓶子的半径为 r, 所以每瓶饮料的利润为： r (0 ， 2) 2 (2 ， 6] f ' (r) 0 f (r) - + 减函数↘ 增函数↗ -1.07 p 因此，当 r>2 时， f′(r)>0, 它表示 f(r) 单调递增，即半径越大，利润越高； 当 r<2 时， f′(r)<0, 它表示 f(r) 单调递减，即半径越大，利润越低 . Ⅰ .半径为 2cm 时，利润最小 , 这时 f(2)<0, 表示此种瓶内饮料的利润还不够瓶子的成本，此时利润是负值； Ⅱ. 半径为 6cm 时，利润最大 . 2 3 从图中，你还能看出什么吗？ 当 0 ＜ r ＜ 3 时，利润为负值；当 r ＝ 3 时，利润为零；当 r ＞ 3 时，利润为正值，并随着瓶子半径的增大利润也相应增大 . 例 3 磁盘的最大存储量问题 计算机把 信息 存储在磁盘上 . 磁盘是带有磁性介质的 圆盘，并 由 操作系统将其格式化成磁道和扇区 . 磁道 是指不同半径所构成的同心 圆 轨道，扇区是指被 圆 心角 分割所成的扇形区域 . 磁道上的定长弧可作为基本 存储单元，根据其磁化与否可分别 记录数据 0 或 1 ，这个基本单元 通常称为比特（ bit ） . 为了保障磁盘的分辨率，磁道之间的宽度必须大于 m ， 每比特所占用的磁道长度不得小于 n. 为了数据检索 便利，磁盘格式化时要求所有磁道要具有相同的比特数 . 问题：现有一张半径为 R 的磁盘，它的存储区是半径 介于 r 与 R 之间的环形区域． ⑴是不是 r 越小，磁盘的存储量越大？ ⑵ r 为多少时，磁盘具有最大存储量 （最外面的磁道不存储任何信息）？ 解： 由题意知：存储量 = 磁道数 × 每磁道的比特数 . 设存储区的半径介于 r 与 R 之间，由于磁道之间的 宽度必须大于 m ，且最外面的磁道不存储任何信息， 故磁道数最多可达 . 由于每条磁道上的比特数 相同，为获得最大存储量，最内一条磁道必须装满， 即每条磁道上的比特数可达 . 所以磁盘总存储量 (1) 它是一个关于 r 的二次函数，从函数解析式上可以 判断，不是 r 越小，磁盘的存储量越大． (2) 为求 的最大值，计算 令 ，解得 当 时， ；当 时， ． 因此当 时，磁盘具有最大存储量 , 此时最大存储量为 　　 解决优化问题的方法之一：通过搜集大量的统计数据，建立与其相应的数学模型，再通过研究相应函数的性质，提出优化方案，使问题得到解决．在这个过程中，导数往往是一个有利的工具，其基本思路如以下流程图所示 : 优化问题 用函数表示数学问题 用导数解决数学问题 优化问题的答案 建立数学模型 解决数学 模型 作答 一、选择题 1 ．三次函数当 x ＝ 1 时，有极大值 4 ；当 x ＝ 3 时， 有极小值 0 ，且函数过原点，则此函数是（ ） A ． y ＝ ＋ 6 ＋ 9x B ． y ＝ － 6 ＋ 9x C ． y ＝ － 6 － 9x D ． y ＝ ＋ 6 － 9x B 解： f′(x) ＝ － 3b ＝ 3( － b) ，令 f′(x) ＝ 0 ，即 － b ＝ 0 ， 由已知可得 b>0 ， ∴ x ＝ 或－ ( 舍去 ) ， 又 0< <1 ，∴ 00 D ． b< A D C 二、填空题 5 ．面积为 S 的一切矩形中，其周长最小的是 ． 6. 在边长为 60cm 的正方形铁片的四角上切去相等的正方形，再把它的边沿虚线折起，做成一个无盖的方底箱子，箱底的边长是多少时，箱子的容积最大？最大容积是多少？ 解： 设箱高为 xcm ，则箱底边长为 (60 － 2x)cm ，则得箱子容积 V 是 x 的函数， V(x) ＝ (60 － 2x) 2 · x(00 ， 当 10