1. 您所在位置：首页 > 中小学教育 > 高中教育 > 教案 > 2013浙江卷（文）数学试题

2013浙江卷（文）数学试题 7页

  • 484.50 KB
  • 2021-06-15 发布

2013浙江卷（文）数学试题

  • 7页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
‎2013·浙江卷(文科数学)‎ ‎　　　　　　　　　　　　　　　　　　　‎ ‎1． 设集合S＝{x|x>－2}，T＝{x|－4≤x≤1}，则S∩T＝(　　)‎ A．[－4，＋∞) B．(－2，＋∞)‎ C．[－4，1] D．(－2，1]‎ ‎1．D　[解析] 从数轴可知，S∩T＝(－2，1]．所以选择D.‎ ‎2． 已知i是虚数单位，则(2＋i)(3＋i)＝(　　)‎ A．5－5i B．7－5i C．5＋5i D．7＋5i ‎2．C　[解析] (2＋i)(3＋i)＝6－1＋i(2＋3)＝5＋5i.所以选择C.‎ ‎3． 若α∈，则“α＝0”是“sin αf(1)，则(　　)‎ A．a>0，4a＋b＝0 B．a<0，4a＋b＝0‎ C．a>0，2a＋b＝0 D．a<0，2a＋b＝0‎ ‎7．A　[解析] 若f(0)＝f(4)，则函数f(x)的图像关于直线x＝2对称，则－＝2，则4a＋b＝0，而f(0)＝f(4)>f(1)，故开口向上，所以a>0，4a＋b＝0.所以选择A.‎ ‎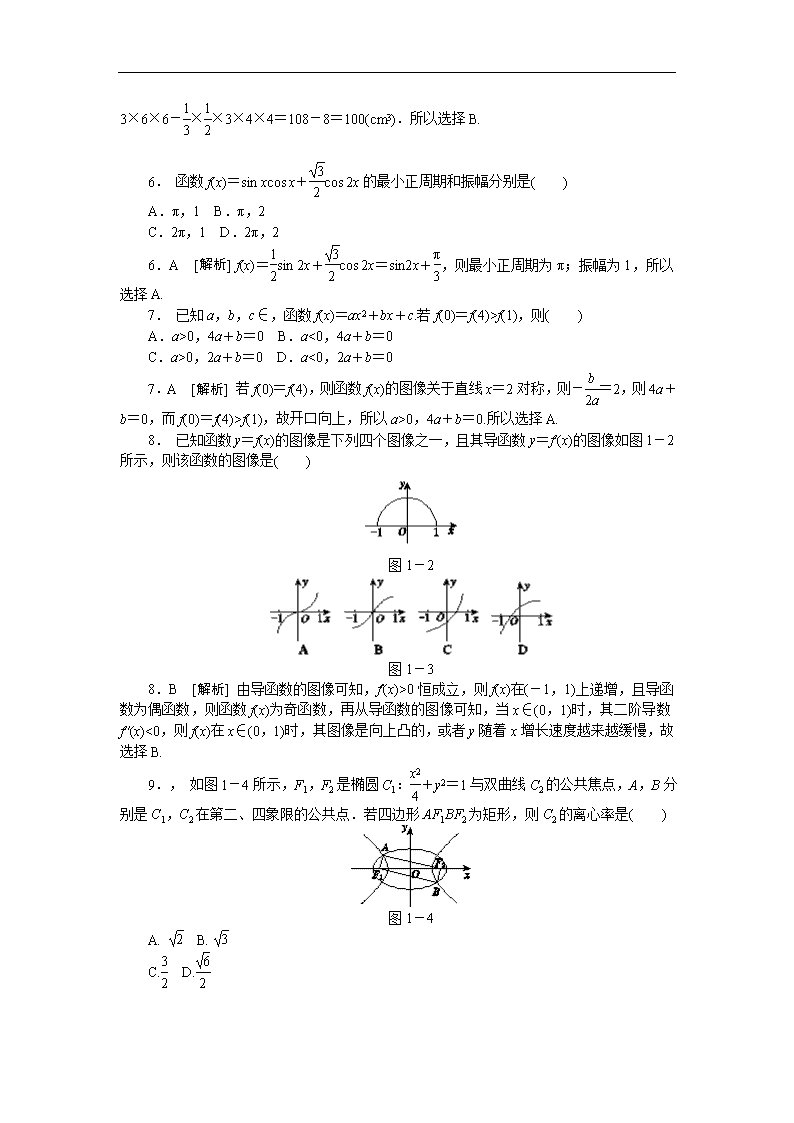8． 已知函数y＝f(x)的图像是下列四个图像之一，且其导函数y＝f′(x)的图像如图1－2所示，则该函数的图像是(　　)‎ 图1－2‎ 图1－3‎ ‎8．B　[解析] 由导函数的图像可知，f′(x)>0恒成立，则f(x)在(－1，1)上递增，且导函数为偶函数，则函数f(x)为奇函数，再从导函数的图像可知，当x∈(0，1)时，其二阶导数f″(x)<0，则f(x)在x∈(0，1)时，其图像是向上凸的，或者y随着x增长速度越来越缓慢，故选择B.‎ ‎9．， 如图1－4所示，F1，F2是椭圆C1：＋y2＝1与双曲线C2的公共焦点，A，B分别是C1，C2在第二、四象限的公共点．若四边形AF1BF2为矩形，则C2的离心率是(　　)‎ 图1－4‎ A. B. C. D. ‎9．D　[解析] 设双曲线实半轴长为a，焦半距为c，|AF1|＝m，|AF2|＝n，由题意知c＝，2mn＝(m＋n)2－(m2＋n2)＝4，(m－n)2＝m2＋n2－2mn＝8，2a＝m－n＝2 ，a＝，则双曲线的离心率e＝＝＝，选择D.‎ ‎10． 设a，b∈，定义运算“∧”和“∨”如下：‎ a∧b＝　a∨b＝ 若正数a，b，c，d满足ab≥4，c＋d≤4，则(　　)‎ A．a∧b≥2，c∧d≤2 B．a∧b≥2，c∨d≥2‎ C．a∨b≥2，c∧d≤2 D．a∨b≥2，c∨d≥2‎ ‎10．C　[解析] 从定义知，a∧b＝min(a，b)，即求a，b中的最小值；a∨b＝max(a，b)，即求a，b中的最大值；假设02，d>2，则c＋d>4，与已知c＋d≤4相矛盾，则假设不成立，故min(a，b)≤2，即c∧d≤2.故选择C.‎ ‎11． 已知函数f(x)＝ .若f(a)＝3，则实数a＝ ________．‎ ‎11．10　[解析] f(a)＝＝3.则a－1＝9，a＝10.‎ ‎12． 从3男3女共6名同学中任选2名(每名同学被选中的机会均等)，这2名都是女同学的概率等于________．‎ ‎12.　[解析] 设选2名都是女同学的事件为A，从6名同学中选2名，共有15种情况，而从3名女生中选2名，有3种情况，所以P(A)＝＝.‎ ‎13． 直线y＝2x＋3被圆x2＋y2－6x－8y＝0所截得的弦长等于________．‎ ‎13．4 　[解析] 圆的标准方程为(x－3)2＋(y－4)2＝25，圆心到直线的距离为d＝＝，所以弦长为2＝2＝4 .‎ ‎14． 若某程序框图如图1－5所示，则该程序运行后输出的值等于________．‎ 图1－5‎ ‎14.　[解析] S＝1＋＋＋…＋＝1＋1－＋－＋…＋－＝1＋1－＝2－ ‎＝.‎ ‎15． 设z＝kx＋y，其中实数x，y满足若z的最大值为12，则实数k＝________．‎ ‎15．2　[解析] 不等式组表示的可行区域为如图所示的三角形ABC及其内部，A(2，0)，B(4，4)，C(2，3)，要使z的最大值为12，只能经过B点，此时12＝4k＋4，k＝2.‎ ‎16． 设a，b∈，若x≥0时恒有0≤x4－x3＋ax＋b≤(x2－1)2，则ab＝________．‎ ‎16．－1　[解析] 当x＝1时，0≤a＋b≤0，则a＋b＝0，b＝－a，令f(x)＝(x2－1)2－(x4－x3＋ax－a)＝x3－2x2－ax＋a＋1，则f(x)≥0在x≥0时恒成立，f(1)＝1－2－a＋a＋1＝0，则x＝1应为极小值点，f′(x)＝3x2－4x－a，故f′(1)＝0，a＝－1，b＝1，ab＝－1.‎ ‎17． 设，为单位向量，非零向量＝x＋y，x，y∈若，的夹角为，则的最大值等于________．‎ ‎17．2　[解析] ＝＝＝＝＝≤＝2.‎ ‎18． 在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2asin B＝ b.‎ ‎(1)求角A的大小；‎ ‎(2)若a＝6，b＋c＝8，求△ABC的面积．‎ ‎18．解：(1)由2asin B＝ b及正弦定理＝，得 sin A＝.因为A是锐角，所以A＝.‎ ‎(2)由余弦定理a2＝b2＋c2－2bc cos A 得b2＋c2－bc＝36.又b＋c＝8，所以bc＝.‎ 由三角形面积公式S＝bcsin A，得△ABC的面积为.‎ ‎19． 在公差为d的等差数列{an}中，已知a1＝10，且a1，2a2＋2，5a3成等比数列．‎ ‎(1)求d，an ；‎ ‎(2)若d<0，求|a1|＋|a2|＋|a3|＋…＋|an|.‎ ‎19．解：(1)由题意得5a3·a1＝(2a2＋2)2，‎ 即d2－3d－4＝0.‎ 故d＝－1或d＝4.所以an＝－n＋11，n∈*或 an＝4n＋6，n∈*.‎ ‎(2)设数列{an}的前n项和为Sn，因为d<0，由(1)得d＝－1，an＝－n＋11，则 当n≤11时，‎ ‎|a1|＋|a2|＋|a3|＋…＋|an|＝Sn＝－n2＋n.‎ 当n≥12时，|a1|＋|a2|＋|a3|＋…＋|an|＝－Sn＋2S11＝n2－n＋110.‎ 综上所述，‎ ‎|a1|＋|a2|＋|a3|＋…＋|an|‎ ‎＝ ‎20． 如图1－6所示，在四棱锥P－ABCD中，PA⊥平面ABCD，AB＝BC＝2，AD＝CD＝ ，PA＝ ，∠ABC＝120°，G为线段PC上的点．‎ ‎(1)证明：BD⊥平面APC；‎ ‎(2)若G为PC的中点，求DG与平面APC所成的角的正切值；‎ ‎(3)若G满足PC⊥平面BGD，求的值．‎ 图1－6‎ ‎20．解：(1)证明：设点O为AC，BD的交点．‎ 由AB＝BC，AD＝CD，得BD是线段AC的中垂线．‎ 所以O为AC的中点，BD⊥AC.‎ 又因为PA⊥平面ABCD，BD⊂平面 ABCD，‎ 所以PA⊥BD.‎ 所以BD⊥平面APC.‎ ‎(2)联结OG.由(1)可知OD⊥平面APC，则DG在平面APC内的射影为OG，所以∠OGD是DG与平面APC所成的角．‎ 由题意得OG＝PA＝.‎ 在△ABC中，‎ AC＝＝2 ，‎ 所以OC＝AC＝.‎ 在直角△OCD中，OD＝＝2.‎ 在直角△OGD中，tan∠OGD＝＝.‎ 所以DG与平面APC所成的角的正切值为.‎ ‎(3)因为PC⊥平面BGD，OG⊂平面BGD，所以PC⊥OG.‎ 在直角△PAC中，得PC＝，‎ 所以GC＝＝.‎ 从而PG＝，所以＝.‎ ‎21． 已知a∈，函数f(x)＝2x3－3(a＋1)x2＋6ax.‎ ‎(1)若a＝1，求曲线y＝f(x)在点(2，f(2))处的切线方程；‎ ‎(2)若|a|>1，求f(x)在闭区间[0，2|a|]上的最小值．‎ ‎21．解：(1)当a＝1时， f′(x)＝6x2－12x＋6，所以f′(2)＝6.‎ 又因为f(2)＝4，所以切线方程为y＝6x－8.‎ ‎(2)记g(a)为f(x)在闭区间[0，2|a|]上的最小值．‎ f′(x)＝6x2－6(a＋1)x＋6a＝6(x－1)(x－a)．‎ 令f′(x)＝0，得x1＝1，x2＝a.‎ 当a>1时，‎ x ‎0‎ ‎(0，1)‎ ‎1‎ ‎(1，a)‎ a ‎(a，2a)‎ ‎2a f′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ ‎0‎ 单调 递增 极大值 ‎3a－1‎ 单调 递减 极小值 a2(3－a)‎ 单调 递增 ‎4a3‎ 比较f(0)＝0和f(a)＝a2(3－a)的大小可得 g(a)＝ 当a<－1时，‎ x ‎0‎ ‎(0，1)‎ ‎1‎ ‎(1，－2a)‎ ‎－2a f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ ‎0‎ 单调 递减 极小值 ‎3a－1‎ 单调 递增 ‎－28a3－24a2‎ 得g(a)＝3a－1.‎ 综上所述，f(x)在闭区间[0，2|a|]上的最小值为 g(a)＝ 图1－1‎ ‎22． 已知抛物线C的顶点为O(0，0)，焦点为F(0，1)．‎ ‎(1)求抛物线C的方程；‎ ‎(2)过点F作直线交抛物线C于A，B两点，若直线AO，BO分别交直线l：y＝x－2于M，N两点，求|MN|的最小值．‎ ‎22．解：(1)由题意可设抛物线C的方程为x2＝2py(p>0)，则＝1，p＝2，所以抛物线C的方程为x2＝4y.‎ ‎(2) 设A(x1，y1)，B(x2，y2)，直线AB的方程为y＝kx＋1.‎ 由消去y，整理得x2－4kx－4＝0.‎ 所以x1＋x2＝4k，x1x2＝－4.‎ 从而|x1－x2|＝4 .‎ 由 解得点M的横坐标xM＝＝＝.‎ 同理点N的横坐标xN＝.‎ 所以|MN|＝ |xM－xN|‎ ‎＝ ‎＝8 ‎＝.‎ 令4k－3＝t，t≠0，则k＝.‎ 当t>0时，|MN|＝2 >2 ；‎ 当t<0时，|MN|＝2 ≥ .‎ 综上所述，当t＝－，即k＝－时，|MN|的最小值是 .‎

您可能关注的文档

相关文档

最近下载