2017-2018学年内蒙古北京八中乌兰察布分校高二下学期期中考试数学（理）试题 Word版 8页

内蒙古北京八中乌兰察布分校 ‎2017-2018学年第二学期期中考试 高二年级数学试题（理）‎ ‎（命题人:徐岳 审核人: 柴树山 分值:150 时间：120分钟）‎ 注意事项：‎ ‎ 1.答卷前，考生务必将自己的姓名、考号填写在答题卡上。‎ ‎ 2.将答案写在答题卡上。写在本试卷上无效。‎ ‎ 3.考试结束后，将答题卡交回。‎ ‎（Ⅰ）卷 一、选择题（本大题共12小题，每小题5分，共60分）‎ 1. 设，其中是实数，则 A. 1 B. C. D. 2‎ 2. 复平面内表示复数的点位于 A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3. 六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有 A. 192种 B. 216种 C. 240种 D. 288种 4. 设，则 A. 既是奇函数又是减函数 B. 既是奇函数又是增函数 C. 是有零点的减函数 D. 是没有零点的奇函数 5. 曲线在点处切线的斜率等于 A. 2e B. e C. 2 D. 1‎ 6. 定积分的值为 A. B. C. e D. ‎ 7. 安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1‎ 人完成，则不同的安排方式共有 A. 12种 B. 18种 C. 24种 D. 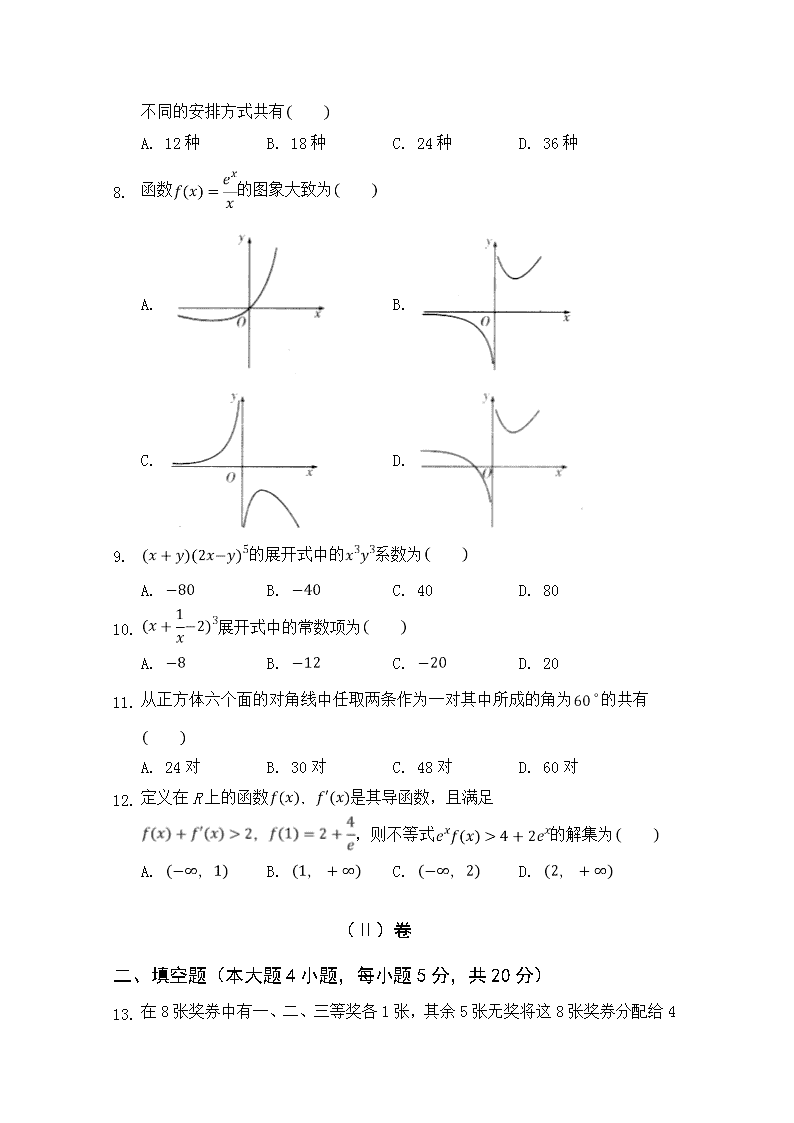36种 1. 函数的图象大致为 A. B. C. D. ‎ 2. 的展开式中的系数为 A. B. C. 40 D. 80‎ 3. 展开式中的常数项为 A. B. C. D. 20‎ 4. 从正方体六个面的对角线中任取两条作为一对其中所成的角为的共有 A. 24对 B. 30对 C. 48对 D. 60对 5. 定义在R上的函数是其导函数，且满足，则不等式的解集为 A. B. C. D. ‎ ‎（Ⅱ）卷 二、填空题（本大题4小题，每小题5分，共20分）‎ 6. 在8张奖券中有一、二、三等奖各1张，其余5张无奖将这8张奖券分配给4‎ 个人，每人2张，不同的获奖情况有______ 种用数字作答．‎ 1. 已知，则______．‎ 2. 用6种不同颜色把图中A、B、C、D四块区域涂色，允许用同一颜色涂不同区域，但相邻区域不能涂同一颜色，不同的涂法共有______种用数字作答．‎ 3. 某校在一天的8节课中安排语文、数学、英语、物理、化学、选修课与2节自修课，其中第1节只能安排语文、数学、英语三门中的一门，第8节只能安排选修课或自修课，且选修课与自修课、自修课与自修课均不能相邻，则所有不同的排法共有______ 种结果用数字表示 三、解答题（本大题6小题，共70分）‎ 4. ‎（10分）抛物线，直线所围成的图形的面积． ‎ 5. ‎（12分）有4名男生，3名女生排成一排： （1）从中选出3人排成一排，有多少种排法？ （2）若男生甲不站排头，女生乙不站在排尾，则有多少种不同的排法？ （3）要求女生必须站在一起，则有多少种不同的排法？ （4）若3名女生互不相邻，则有多少种不同的排法？ ‎ 6. ‎（12分）在二项式的展开式中，前三项系数成等差数列． （1）求展开式中的常数项； （2）求展开式中系数最大的项． ‎ 1. ‎（12分）已知函数，其中，且曲线在点处的切线垂直于直线 （1）求a的值； （2）求函数的单调区间与极值． ‎ ‎21.（12分）设，求： ； ； ； ． ‎ ‎22.（12分）设函数． （1）讨论的单调性； （2）证明当时，‎ ‎； （3）设，证明当时，． ‎ ‎2017-2018学年第二学期期中考试 高二年级数学试题答案（理）‎ 一、 选择题（本大题共12小题，共60分）‎ 题号 ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ 4 ‎ ‎ 5‎ ‎ 6‎ ‎ 7‎ ‎ 8‎ ‎ 9‎ ‎ 10‎ ‎ 11‎ ‎ 12‎ 答案 ‎ B ‎ C ‎ ‎ B ‎ B ‎ C ‎ C ‎ D ‎ ‎ B ‎ C ‎ C ‎ C ‎ B ‎ ‎ ‎ ‎ 二、填空题（本大题共4小题，共20分）‎ ‎13. 60 14. 15. 480 16. 1296． 三、解答题（本大题共6小题，共70分）‎ ‎17.(10分)【答案】解：由，得抛物线与轴的交点坐标是和，所求图形分成两块， 分别用定积分表示面积． 故面积 ．‎ ‎18.（12分）【答案】解：由题意可得从中选出3人排成一排的方法种数为 间接法：总的方法种数共，去掉男生甲站排头，女生乙站在排尾 共，而其中重复的为男生甲站排头，同时女生乙站在排尾的 故总的方法种数为： 捆绑法：把3名女生看作1个元素与其它排列共种， 再对3名女生作调整共种，由分步计数原理可得共 插空法：先排4名男生共种，在把3名女生插到所产生的5个空位， 共种，由分步计数原理可得共 ‎ ‎19（12分）【答案】解：二项式的展开式中，前三项系数分别为， 再根据前三项系数成等差数列，可得，求得或舍去． 故二项式的展开式的通项公式为． 令，求得，可得展开式的常数项为．Ⅱ设第项的系数最大，则由，求得，即， 故或，故第三项或第四项的系数最大，再利用通项公式可得系数最大的项为 ‎．‎ ‎ ‎ ‎20（12分）【答案】解：Ⅰ， ， 曲线在点处的切线垂直于直线 ， 解得：． Ⅱ由Ⅰ知：， ， 令， 解得，或舍， 当时，，当时，， 故函数的单调递增区间为； 单调递减区间为； 当时，函数取极小值．‎ ‎ ‎ ‎21（12分）【答案】解：， 令，可得 ． 在中，令，可得． 在，中，令，可得， 可得． 可得， ．‎ ‎22（12分）【答案】解：函数的导数为， 由，可得；由，可得． 即有的增区间为；减区间为； 证明：当时，，即为． 由可得在递减， 可得，即有； 设， 当时，，可得递增，即有， 即有，则原不等式成立； 证明：设 ‎， 可令，可得， 由，可得，即， 由可得恰有一解，设为是的最大值点，且， 由，且在递增，在递减， 可得成立， 则，当时，．‎ ‎ ‎