江西省南昌市八一中学2019-2020学年高二下学期期中考试数学（文）试题 8页

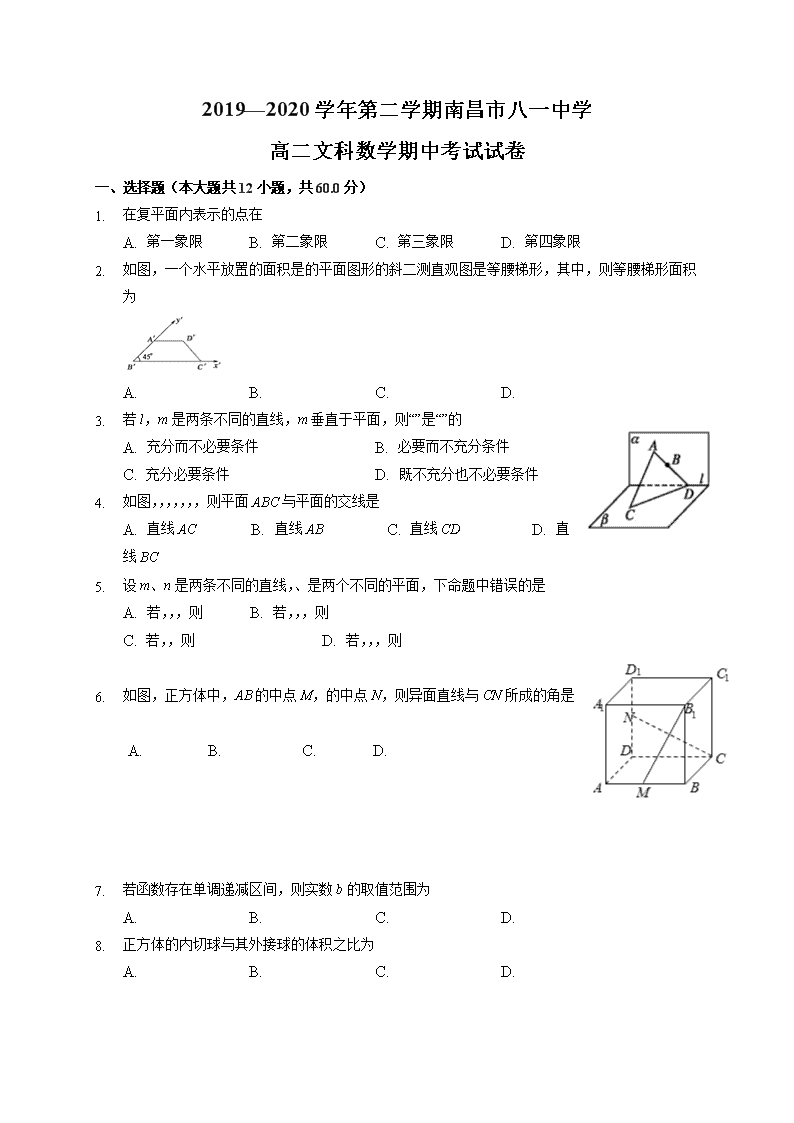
‎2019—2020学年第二学期南昌市八一中学 高二文科数学期中考试试卷 一、选择题（本大题共12小题，共60.0分）‎ 1. 在复平面内表示的点在   ‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2. 如图，一个水平放置的面积是的平面图形的斜二测直观图是等腰梯形，其中，则等腰梯形面积为 ‎ A. B. C. D. ‎ 3. 若l，m是两条不同的直线，m垂直于平面，则“”是“”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 4. 如图，，，，，，，则平面ABC与平面的交线是    ‎ A. 直线AC B. 直线AB C. 直线CD D. 直线BC 5. 设m、n是两条不同的直线，、是两个不同的平面，下命题中错误的是 A. 若，，，则 B. 若，，，则 C. 若，，则 D. 若，，，则 6. 如图，正方体中，AB的中点M，的中点N，则异面直线与CN所成的角是 A. B. C. D. ‎ 7. 若函数存在单调递减区间，则实数b的取值范围为 A. B. C. D. ‎ 8. 正方体的内切球与其外接球的体积之比为     ‎ A. B. C. D. 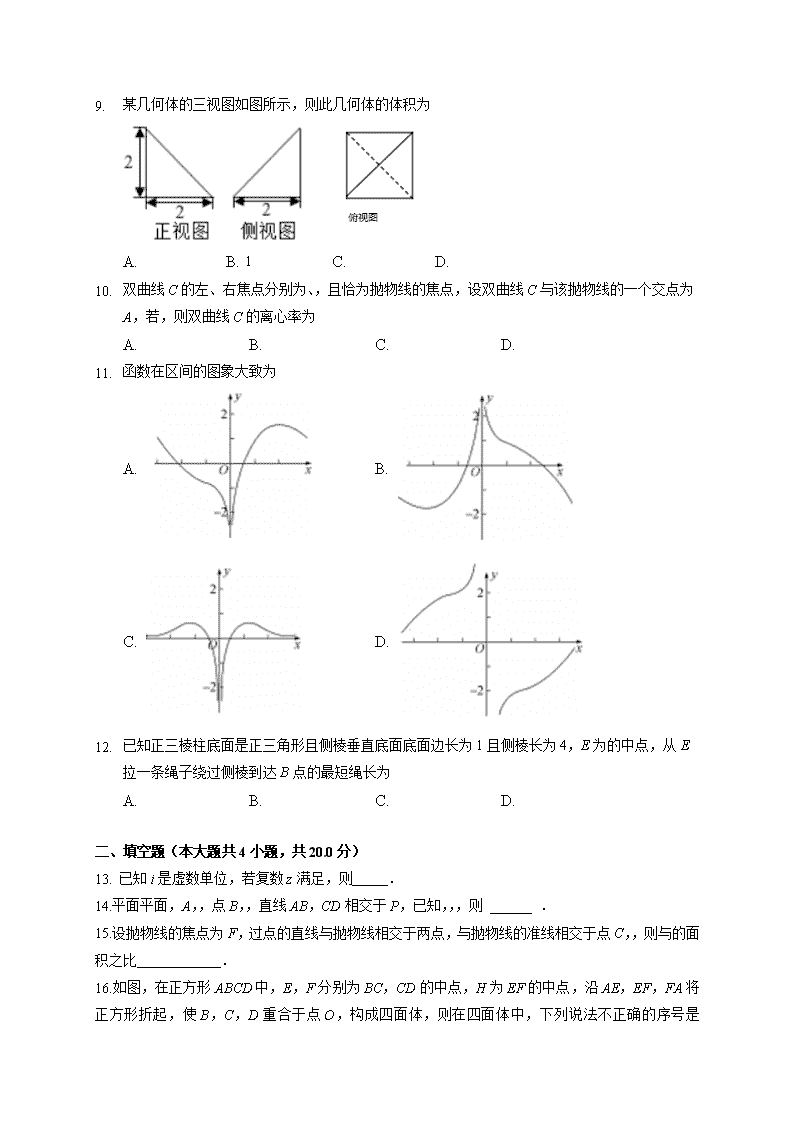‎ 1. 某几何体的三视图如图所示，则此几何体的体积为 A. B. 1 C. D. ‎ 2. 双曲线C的左、右焦点分别为、，且恰为抛物线的焦点，设双曲线C与该抛物线的一个交点为A，若，则双曲线C的离心率为    ‎ A. B. C. D. ‎ 3. 函数在区间的图象大致为    ‎ A. B. C. D. ‎ 4. 已知正三棱柱底面是正三角形且侧棱垂直底面底面边长为1且侧棱长为4，E为的中点，从E拉一条绳子绕过侧棱到达B点的最短绳长为    ‎ A. B. C. D. ‎ 二、填空题（本大题共4小题，共20.0分）‎ ‎13. 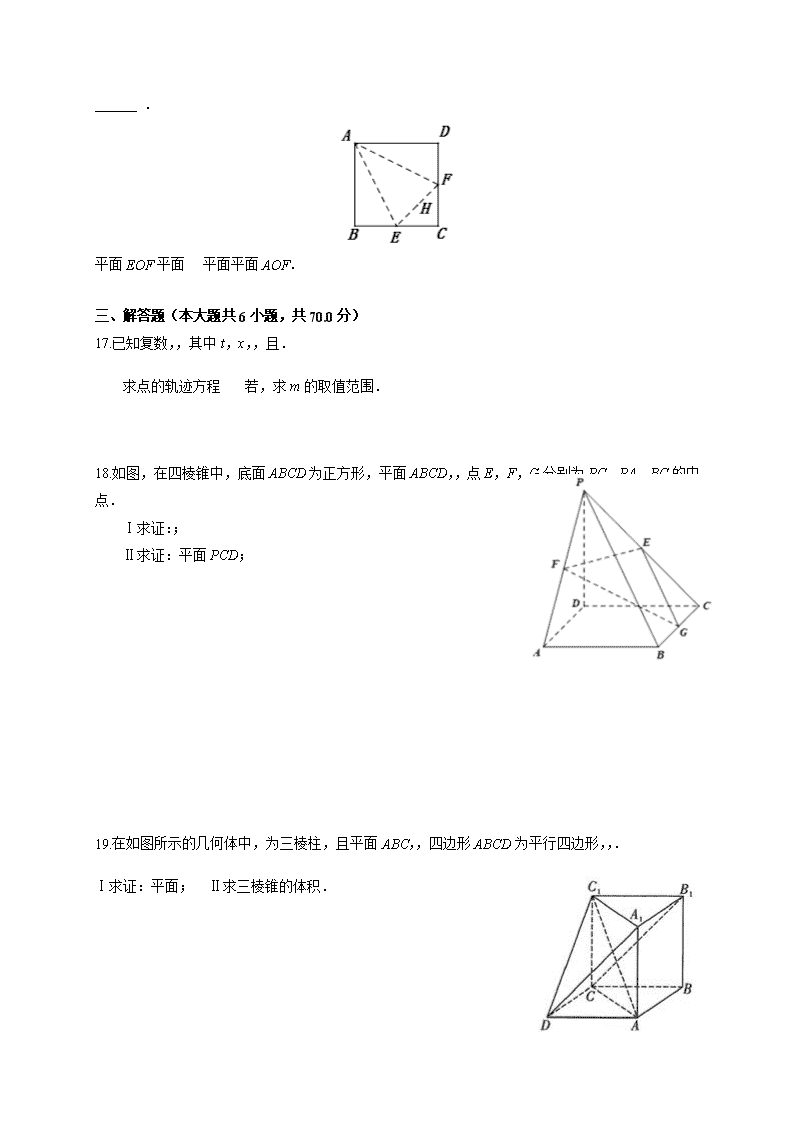已知i是虚数单位，若复数z满足，则          ．‎ ‎14.平面平面，A，，点B，，直线AB，CD相交于P，已知，，，则 ______ ．‎ ‎15.设抛物线的焦点为F，过点的直线与抛物线相交于两点，与抛物线的准线相交于点C，，则与的面积之比____________．‎ ‎16.如图，在正方形ABCD中，E，F分别为BC，CD的中点，H为EF的中点，沿AE，EF，FA将正方形折起，使B，C，D重合于点O ‎，构成四面体，则在四面体中，下列说法不正确的序号是______ ．‎ 平面EOF 平面     平面平面AOF．‎ 三、解答题（本大题共6小题，共70.0分）‎ ‎17.已知复数，，其中t，x，，且．‎ 求点的轨迹方程 若，求m的取值范围．‎ ‎18.如图，在四棱锥中，底面ABCD为正方形，平面ABCD，，点E，F，G分别为PC，PA，BC的中点． Ⅰ求证：； Ⅱ求证：平面PCD； ‎ ‎19.在如图所示的几何体中，为三棱柱，且平面ABC，，四边形ABCD为平行四边形，，．‎ Ⅰ求证：平面； Ⅱ求三棱锥的体积． ‎ ‎20.已知椭圆的短轴长为4，离心率为，斜率不为0的直线l与椭圆恒交于A，B两点，且以AB为直径的圆过椭圆的右顶点M． 求椭圆的标准方程； 直线l是否过定点，如果过定点，求出该定点的坐标；如果不过定点，请说明理由．‎ ‎21.如图，在四棱锥中，平面ABCD，底面ABCD为菱形，且，E为CD的中点． 求证：平面平面PAE； 棱PB上是否存在点F，使得平面PAE？说明理由．‎ ‎ ‎ ‎22.已知函数，其中e是自然对数的底数． 当时，求函数的极值； 若，不等式恒成立，求实数a的取值范围．‎ 高二文科数学参考答案 一、选择题：BABCD DBCCA AB 二、填空题：13. 14.2或34 15. 16. 三、解答题： 17.【答案】解：根据复数相等的充要条件得， 将代入，得，即， 因此，所求点P的轨迹方程为．‎ 由，知点P的轨迹是一个圆，其圆心为，半径为， 当直线与圆有公共点时，， 即，得， 所以所求m的取值范围为 ‎19.【答案】Ⅰ证明：为三棱柱，且平面ABC，， 是正方形，C. 由，得， 四边形ABCD为平行四边形，， ， ，则， ， 平面ABC，平面ABC， ， 又，AC、平面， 平面，且平面， ，则， ，、平面， 平面； Ⅱ解：易知， 由Ⅰ 得，平面， 则平面， 三棱锥的体积： ． 20.【答案】解：由题，， 所以椭圆的标准方程为． 由题设直线l：，，，， 联立直线方程和椭圆方程，得， ，，． 因为以AB为直径的圆过椭圆的右顶点M， 所以，‎ 即或4， 又当时，直线l过椭圆右定点，此时直线MA与直线MB不可能垂直， ， 直线过定点． 21.【答案】解：证明：因为底面ABCD是菱形且，所以为正三角形， 因为E为CD的中点，所以， 因为，所以； 因为平面ABCD，平面ABCD，所以； 因为所以平面PAB， 因为平面PAE，所以平面平面PAE． 解：存在点F为PB中点时，满足平面PAE；理由如下： 分别取PB，PA的中点F，G，连接CF，FG，EG， 在三角形PAB中，，且， 在菱形ABCD中，E为CD中点，所以且， 所以且，即四边形CEGF为平行四边形， 所以； 又平面PAE，平面PAE，所以平面PAE ‎． 22.【答案】解：当时，，定义域为； 求导得：， 方程的根为或， 列表得：‎ x ‎0‎ ‎0‎ 极大值 极小值 由上表可以，． ， 由条件知，对恒成立， 令， ， ． 当时，， 在上单调递减， ， 即， 在上单调递减， ， 则若在上恒成立， 则需，， 即实数a的取值范围是． ‎