2018-2019学年吉林省白城市通榆县第一中学高二上学期第二次质检数学试题 Word版 8页

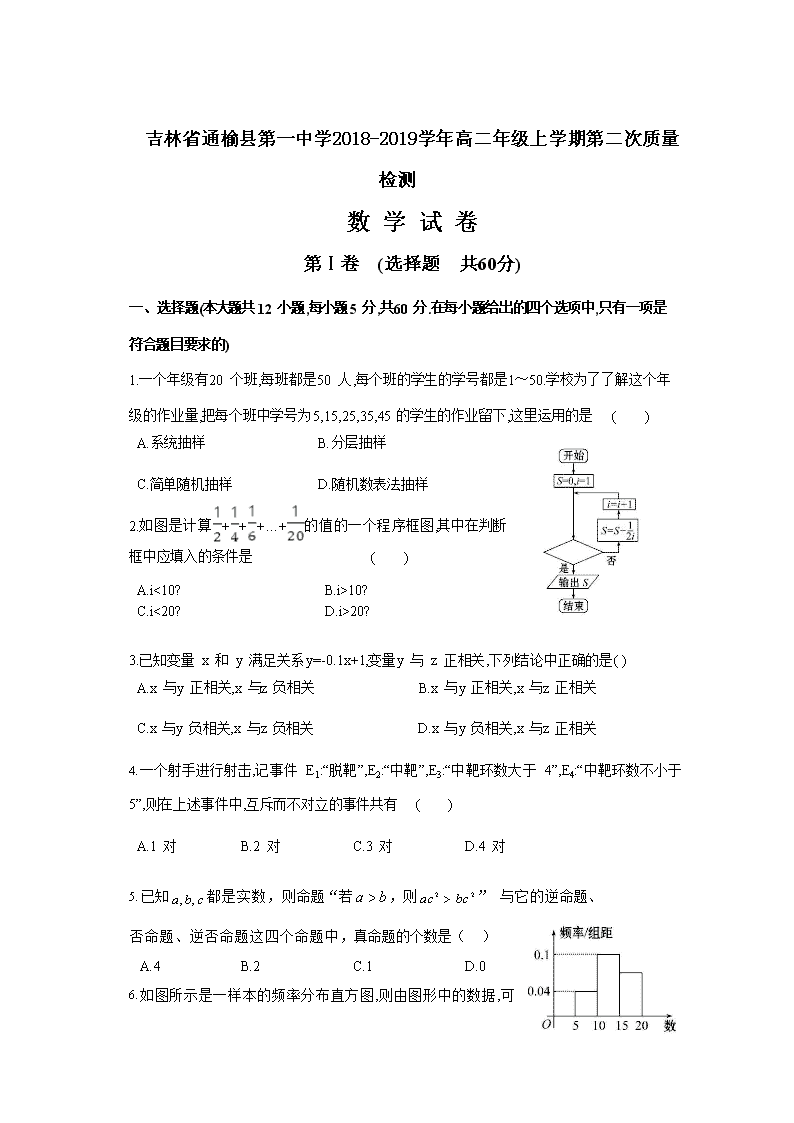
吉林省通榆县第一中学2018-2019学年高二年级上学期第二次质量检测 数 学 试 卷 第Ⅰ卷　(选择题　共60分) ‎ 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的)‎ ‎1.一个年级有 20 个班,每班都是 50 人,每个班的学生的学号都是 1～50.学校为了了解这个年级的作业量,把每个班中学号为 5,15,25,35,45 的学生的作业留下,这里运用的是 ( )‎ A.系统抽样 B.分层抽样 C.简单随机抽样 D.随机数表法抽样 ‎2.如图是计算 + + +…+ 的值的一个程序框图,其中在判断框中应填入的条件是 ( )‎ A.i<10? B.i>10?‎ C.i<20? D.i>20?‎ ‎3.已知变量x 和y 满足关系 y=-0.1x+1,变量 y 与z 正相关,下列结论中正确的是( )‎ A.x 与 y 正相关,x 与 z 负相关 B.x 与 y 正相关,x 与 z 正相关 C.x 与 y 负相关,x 与 z 负相关 D.x 与 y 负相关,x 与 z 正相关 4. 一个射手进行射击,记事件 E1:“脱靶”,E2:“中靶”,E3:“中靶环数大于 4”,E4:“中靶环数不小于 ‎5”,则在上述事件中,互斥而不对立的事件共有 ( )‎ A.1 对 B.2 对 C.3 对 D.4 对 5. 已知都是实数，则命题“若，则” 与它的逆命题、否命题、逆否命题这四个命题中，真命题的个数是（ ）‎ A.4 B.2 C.1 D.0‎ 6. 如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计 众数与中位数分别是 ( )‎ A.12.5 12.5 B.12.5 13 C.13 12.5 D.13 13‎ 4. 已知直线 y=x+b,b∈[-2,3],则直线在 y 轴上的截距大于 1 的概率为 ( )‎ A. B. C. D.‎ 5. 一袋中装有大小相同的四个球,编号分别为 1,2,3,4,现从中有放回地每次取一个球,共取 2 次, 记“取得两个球的编号和大于或等于 6”为事件 A,则P(A)等于 ( )‎ A. B. C. D.‎ ‎9.某市 2017年各月的平均气温(℃)数据的茎叶图如图:‎ 则这组数据的中位数是 ( )‎ A.19 B.20 C.21.5 D.23‎ ‎10. “”是“函数在区间上为增函数” ‎ 的（ ）‎ A.充分而不必要条件 B.必要而不充分条件 ‎ C.充要条件 D.既不充分也不必要条件 ‎11. 将八进制数135(8)转化为二进制数是（ ）‎ A. 1110101(2) B. 1010101(2) C. 111001(2) D. 1011101(2)‎ ‎12.小莉与小明一起用A,B 两枚均匀的小立方体(立方体的每个面上分别标有数字 1,2,3,4,5,6)‎ 玩游戏,以小莉掷的 A 立方体朝上的数字为 x,小明掷的 B 立方体朝上的数字为 y,来确定点 P(x,y),那么他们各掷一次所确定的点P(x,y)落在已知抛物线 y=-x2+4x 上的概率为 ( )‎ A. B. C. D.‎ 第Ⅱ卷　(非选择题　共90分)‎ 二、填空题(本大题共 4 个小题,每小题 5 分,共 20 分.)‎ ‎13.某校高一年级有 900 名学生,其中女生 400 名.按男女比例用分层抽样的方 法,从该年级学生中抽取一个容量为 45 的样本,则应抽取的男生人数为 .‎ 14. 由不等式组 确定的平面区域记为 Ω1,不等式组确 定的平面区域记为Ω2.在 Ω1 中随机取一点,则该点恰好在 Ω2 内的概率为 .‎ 15. 某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的 频 率 分 布 直 方 图 , 其 中 产 品 净 重 的 范 围 是 [96,106], 样 本 数 据 分[96,98),[98,100),[100,102), [102,104),[104,106],已知样本中产品净重小于 100 克的个数是 36,则样本中净重大于或等于 98 克并且小于 104 克的产品的个数是 .‎ 16. 执行如图的程序框图,若输入 x=9,则输出 y= .‎ 第 15 题图 第 16 题图 三、解答题(本大题共 6 个小题,共 70 分,解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎17.（10分）已知，，若是的一个充分不必要条件，求的取值范围.‎ ‎18.(12 分)(2016·枣庄高一检测)A,B,C,D,E 五位学生的数学成绩x 与物理成绩 y(单位:分)如表:‎ x ‎80‎ ‎75‎ ‎70‎ ‎65‎ ‎60‎ y ‎70‎ ‎66‎ ‎68‎ ‎64‎ ‎62‎ (1) 请根据上表提供的数据,用最小二乘法求出y 关于x 的回归方程 = x+;‎ ‎(参考数值:80×70+75×6 6+70×68+65×64+60×62=23190, 80 ‎ ‎2+752+702+652+602=24750)‎ (1) 若学生 F 的数学成绩为 90 分,试根据(1)求出的回归方程,预测其物理成绩(结果保留整数).‎ ‎(参考公式：)‎ ‎19. (12 分) 随机抽取某高中甲、乙两个班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图所示．]‎ ‎(1)甲班和乙班同学身高的中位数各是多少？并计算甲班样本的方差．‎ ‎(2)现从乙班这10名同学中随机抽取2名身高不低于173 cm的同学，求身高为176 cm的同学被抽中的概率．‎ ‎20. (12 分)设命题实数满足，其中，命题实数满足.‎ ‎（Ⅰ）若，且与均为真，求实数的取值范围.‎ ‎（Ⅱ）若是的必要不充分条件，求实数的取值范围.‎ ‎21. (12 分) 某初级中学共有学生 2000 名,各年级男生、女生人数如表:‎ 初一年级 初二年级 初三年级 女生 ‎373‎ x y 男生 ‎377‎ ‎370‎ z 已知在全校学生中随机抽取 1 名,抽到的是初二年级女生的概率是 0.19.‎ (1) 求 x 的值.‎ (2) 现用分层抽样法在全校抽取 48 名学生,问应在初三年级学生中抽取多少名?‎ (3) 已知 y≥245,z≥245,求初三年级女生比男生多的概率.‎ ‎22.(12 分)高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:‎ (1) 求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中 ‎[80,90)间的矩形的高.‎ (2) 若要从分数在[80,100]之间的学生中任选 2 人进行某项研究,求至少有 1 人分数在[90,100] 之间的概率.‎ 高二数学第二次质量检测答案 ‎1. A. 2.B.3 C.4. B.5. B .6. B.7. B.8. C.9. B.10 A 11.D .12. C.‎ ‎13.25 14. 15.90 16. ‎ ‎17.‎ ‎18.(1)线性回归方程为 =0.36x+40.8.‎ ‎(2)由(1),当x=90 时, =0.36×90+40.8=73.2≈73,‎ 答:预测学生F 的物理成绩为 73 分.‎ ‎19.(1)根据中位数的定义知，‎ 甲班同学身高的中位数是＝169(cm)，‎ 乙班同学身高的中位数是＝171.5(cm)．‎ 根据平均数的公式，计算甲班的平均数 ‎＝×(158＋162＋163＋168＋168＋170＋171＋179＋179＋182)＝170，‎ 甲班样本的方差s＝×[(158－170)2＋(162－170)2＋…＋(182－170)2]＝57.2.‎ ‎(2)设“身高为176 cm的同学被抽中”为事件A.‎ 从乙班10名同学中抽取2名身高不低于173 cm的同学有(181，173)，(181，176)，(181，178)，(181，179)，(179，173)，(179，176)，(179，178)，(178，173)，(178，176)，(176，173)，共10个基本事件，而事件A含有4个基本事件，所以P(A)＝＝.‎ ‎20.解：∵ ，由，得，则真得， .‎ 由，解得，即真得.‎ ‎（1）若解得，若p与q为真，则同时为真，‎ 即，解得，∴实数的取值范围.‎ ‎（2）若p是q的必要不充分条件，即是的充分不必要条件，‎ ‎∴，即，解得.‎ ‎21.(1)x=380(2)初三年级人数为y+z=2000-(373+377+380+370)=500,‎ 现用分层抽样法在全校抽取 48 名学生,应在初三年级学生中抽取的 人数为 ×500=12,即抽取初三年级学生 12 名.‎ ‎(3)记“初三年级女生比男生多”为事件 A, 由(2)知y+z=500,又已知y≥245,z≥245,‎ 则所有的基本事件(前一个数表示女生人数,后一个数表示男生人数) 有(245,255),(246,254),(247,253),…,(255,245),共 11 个.‎ 其中事件A 包含的基本事件(251,249),(252,248),(253,247),‎ ‎(254,246),(255,245),共 5 个,则P(A)= ‎ ‎22.(1)因为分数在[50,60)之间的频数为 2,频率为 0.008×‎ ‎10=0.08,所以高一(1)班参加校生物竞赛的人数为 =25.‎ 分数在[80,90)之间的频数为 25-2-7-10-2=4,频率为 =0.16,[]‎ 所以频率分布直方图中[80,90)间的矩形的高为=0.016.‎ (2) 设“至少有 1 人分数在[90,100]之间”为事件 A,将[80,90)之间的 4 人编号为 1,2,3, 4,[90,100]之间的 2 人编号为 5,6.在[80,100]之间任取 2 人的基本事件有:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),‎ ‎(3,4),(3,5),(3,6),(4,5),( 4,6),(5,6),共 15 个.其中,至少有 1 人分数在[90,100]之间的基本事件有 9 个,根据古典概型概率的计算公式,‎ 得P(A)= ‎