- 911.00 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2019衡水名师原创文科数学专题卷
专题十六 算法、推理与证明、复数
考点49: 算法与程序框图(1-15题,31-35题)
考点50 : 合情推理与演绎推理(16,17题,36,37题)
考点51 : 直接证明与间接证明(18题)
考点52 : 数学归纳法(19题)
考点53 : 复数的概念与运算 (20-30题,38-40题)
一、选择题
1.运行如图所示的程序框图,若输入,则输出的值为( )
A.10 B.11 C.12 D.9
2.阅读如图所示的程序框图,运行相应的程序,输出的结果是( )
A.3 B.11 C.38 D.123
3.如图所示的程序框图中,输出S的值为( )
A.10 B.12 C.15 D.8
4.阅读如图所示的程序框图,运行相应的程序,则输出的值为( )
A.-10 B.6 C.14 D.18
5.执行如图所示程序框图,输出的 ( )
A.3 B.4 C.5 D.6
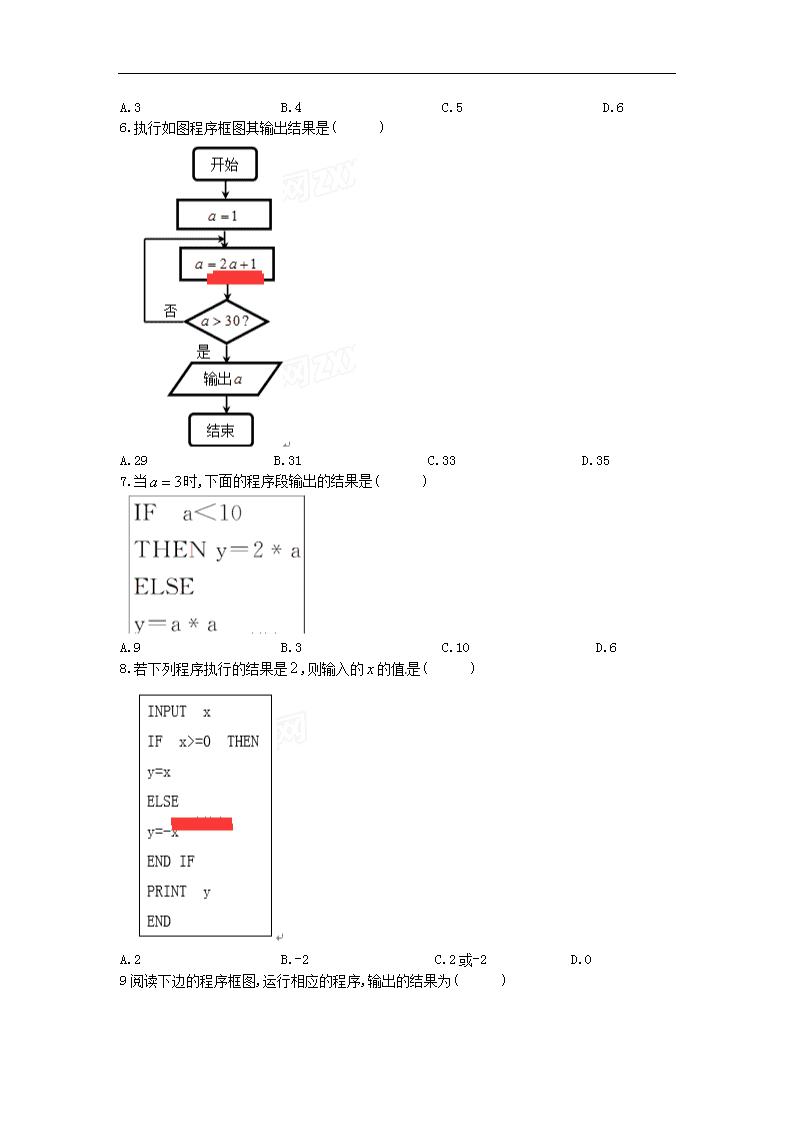
6.执行如图程序框图其输出结果是( )
A.29 B.31 C.33 D.35
7.当时,下面的程序段输出的结果是( )
A.9 B.3 C.10 D.6
8.若下列程序执行的结果是,则输入的的值是( )
A.2 B.-2 C.2或-2 D.0
9阅读下边的程序框图,运行相应的程序,输出的结果为( )
[来
A.
B.
C.
D.
10公元年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )
(参考数据:,,,)
A.
B.
C.
D.
11.执行如图所示的程序框图,则输出的值是值为( )
A.4 B.7 C.9 D.16
12.运行下列程序,若输入的的值分别为,则输入的的值为( )
A.61 B.68 C.75 D.82
13.为计算,设计了下侧的程序框图,则在空白框中应填入( )
A.
B.
C.
D.
14执行下面的程序框图,为使输出的的值小于,则输入的正整数的最小值为( )
A.5
B.4
C.3
D.2
15.用三段论推理:“任何实数的绝对值大于,因为是实数,所以的绝对值大于”,你认为这个推理( )
A.大前提错误 B.小前提错误
C.推理形式错误 D.是正确的
16.用反证法证明“若则或”时,应假设( )
A. 或
B. 且
C.
D.
17.复数满足则 ( )
A.
B.
C.
D.
18.已知,则复数在复平面内对应的点的坐标是( )
A.(-1,-2) B.(-1,2) C.(1,-2) D.(1,2)
19.已知复数满足,则复数对应的点所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
20.复数满足,若复数对应的点为,则点到直线的距离为( )
A.
B.
C.
D.
21.若复数是实数,则的值为( )
A.
B.
C.
D.
22.设复数,在复平面内的对应点关于虚轴对称, ,则 ( )
A.
B.
C.
D.
23.在复平面内,复数,对应的点分别为.若为线段的中点,则 (为坐标原点)对应的复数是( )
A.
B.
C.
D.
24设复数满足,则( )
A.
B.
C.
D.
25.若复数 (为虚数单位),则在复平面内对应的点的坐标是( )
A.
B.
C.
D.
26.设是虚数单位,复数 ( )
A.
B.
C.
D.
27设有下面四个命题
:若复数满足,则;
:若复数满足,则;
:若复数,满足,则
:若复数,则.
其中的真命题为( )
A.,
B.,
C.,
D.,
二、填空题
28.执行如图所示的程序框图,当输入时,输出的值为__________.
29.根据以下伪代码,可知输出的结果为__________.
30.程序框图如图所示,若输入,,,则输出的为__________.
31.如图是一个输出一列数的算法流程图,则这列数的第三项是__________.
32.有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三
人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是__________.
33.用火柴棒摆“金鱼”,如图所示:
按照上面的规律,第条“金鱼”需要火柴棒的根数为__________.
34.已知,,且,则数列前项的和为__________.
35.若,,且为纯虚数,则实数的值为__________
36.已知, (是虚数单位)则__________,__________。
参考答案
一、选择题
1.答案:B
解析:
2.答案:B
解析:
3.答案:C
解析:
4.答案:B
解析:输入不成立;
不成立;
成立,输出,故选B
5.答案:B
解析:依次运行框图中的程序,可得:
第一次, ,不满足条件,继续运行;
第二次, ,不满足条件,继续运行;
第三次, ,不满足条件,继续运行;
第四次, ,满足条件,输出.故选
6.答案:B
解析:第一次循环:;第二次循环:;第三次循环:;第四次循环:;结束循环,输出:;选B.
考点:
循环结构流程图
7.答案:D
解析:因为,所以
8.答案:C
解析:
答案: D
解析: 执行程序框图,第一次循环,,;第二次循环,,;第三次循环,,;第四次循环,,;可得的值呈周期性出现,周期为,时,输出,故选D.
答案: B
解析: 模拟执行程序,可得:,,不满足条件;
,,不满足条件;
,,满足条件,退出循环,
输出的值为.故选
11.答案:C
解析:
12.答案:C
解析:
13.答案:B
解析:由得程序框图先对奇数项累加,偶数项累加,最后再相减.因此在空白框中应填入,故选B.
答案: D
解析: 程序运行过程如下表所示:
初始状态
0
100
1
第1次循环结束
100
-10
2
第2次循环结束
90
1
3
此时首次满足条件,程序需在时跳出循环,即为满足条件的最小值,故选D.
15.答案:A解析:0的绝对值等于0,不大于0,大前提错误.
16.答案:B
解析:用反证法证明“若 则或”时,应先假设且.
故选:B
.
熟记反证法的步骤,直接填空即可反面有多种情况,需一一否定.
此题主要考查了反证法的第一步,解此题关键要懂得反证法的意义及步骤反证法的步骤是:
假设结论不成立;
从假设出发推出矛盾;
假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
17.答案:C
解析:
18.答案:A
解析:由已知有 .复数在复平面内对应的点得坐标为 .故选A.
19.答案:D
解析:表示点,对应的点所在象限是第四象限,选D.
20.答案:D
解析:由得,∴,∴对应的点为,∴所求距离为.
21.答案:A
解析:,
因为复数是实数,所以即,选A
22.答案:C
解析:因为,所以,即,又因为复数,在复平面内的对应点关于虚轴对称,所以,故选C.
23.答案:C
解析:
由复数的几何意义,则
又点为线段的中点
∴点的坐标为
故向量的对应复数.
答案: C
解析: 由题, ,则,故选C。
25.答案:D
解析:
26.答案:D
解析:∵,
,
∴.
答案: B
解析: 令,则由得,所以,故正确;
当时,因为,而知,故不正确;
当时,满足,而,知不正确;
对于,因为实数没有虚部,所以它的共轭复数是它本身,也属于实数,故正确,故选B.
二、填空题
28.答案:
解析:∵,,故答案是.
29.答案:5
解析:第一步: ;第二步: ;第三步: .
30.答案:1024
解析:由程序框图的功能知,该程序执行的是.
31.答案:30
解析:第一次循环: ,;第二次循环: ,;第三次循环: ,;因此这列数的第三项是
32.答案:1和3
解析:丙说他的卡片上的数字之和不是5,所以丙的卡片上的数字要么是1和2,要么是1和3.又乙说他与丙的卡片上相同的数字不是1,所以卡片2和3必定在乙手中.因为甲与乙的卡片上相同的数字不是2,所以甲的卡片上的数字只能是1和3.
33.答案:6n+2
解析:由图形间的关系可以看出,第一个图中有根火柴棒,第二个图中有根火柴棒,第三个图中有根火柴棒,以此类推第个“金鱼”需要火柴棒的根数是,即.
34.答案:-910
解析:由可得,由此可得,解之得.故数列的前项和为.
35.答案:
解析:为纯虚数,
36.答案:5; 2
解析:由题意可得,则,解得,则,.