高中数学选修2-2课件2_2_1_2 42页

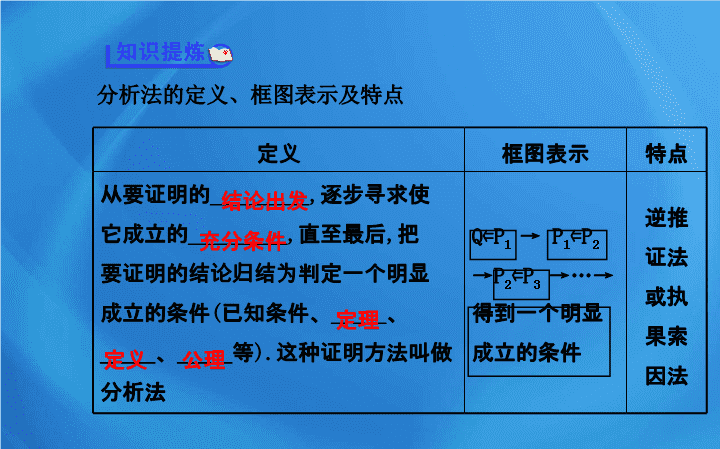
第 2 课时　 分　析　法 问题 引航 1. 分析法的定义是什么 ? 有什么特点 ? 2. 分析法与综合法有什么区别和联系 ? 分析法的定义、框图表示及特点 定义 框图表示 特点 从要证明的 _________, 逐步寻求使 它成立的 _________, 直至最后 , 把 要证明的结论归结为判定一个明显 成立的条件 ( 已知条件、 _____ 、 _____ 、 _____ 等 ). 这种证明方法叫做分析法 Q ⇐ P 1 → P 1 ⇐ P 2 →P 2 ⇐ P 3 →…→ 得到一个明显 成立的条件 逆推证法或执果索因法 结论出发 充分条件 定理 定义 公理 1. 判一判 ( 正确的打 “ √ ” , 错误的打 “ × ” ) (1) 分析法就是从结论推向已知 . 　 ( 　　 ) (2) 分析法的推理过程要比综合法优越 . 　 ( 　　 ) (3) 所有证明的题目均可使用分析法证明 . 　 ( 　　 ) 【 解析 】 (1) 错误 . 分析法又叫逆推证法 , 但不是从结论推向已知 . 而是寻找使结论成立的充分条件的过程 . (2) 错误 . 分析法和综合法各有优缺点 . (3) 错误 . 一般用综合法证明的题目均可用分析法证明 , 但并不是所有的证明题均可使用分析法证明 . 答案 : (1)× 　 (2)× 　 (3)× 2. 做一做 ( 请把正确的答案写在横线上 ) (1) 证明不等式 (a≥2) 成立所用的最适合的方法是 　　　　 . (2) 要证明 A>B, 若用作差比较法 , 只要证明 　　　　 . (3) 在不等边三角形中 ,a 为最大边 , 要想得到 A 为钝角的结论 , 对三边 a,b,c 应满足的条件是 a 2 　　　 b 2 +c 2 ( 填 “ > ”“ < ”“ ≥ ” 或 “ ≤ ” ). 【 解析 】 (1) 由于此式两边都有根号 , 由其特点可用分析法证明此不等式 . 答案 : 分析法 (2) 要证 A>B, 只需证 A-B>0. 答案 : A-B>0 (3) 因为 a 为最大边 , 且 a≠b≠c, 所以要想 A 为钝角 , 只需 cosA<0, 即 cosA= <0, 只需要 b 2 +c 2 b 2 +c 2 . 答案 : > 【 要点探究 】 知识点 分析法 1. 对分析法的四点说明 (1) 思维特点 : 从 “ 未知 ” 看 “ 需知 ” , 逐步靠拢 “ 已知 ” , 其推理过程实际上是逐步寻求结论成立的充分条件的过程 . (2) 思维过程 : 由结果追溯原因 , 即结果←原因 . (3) 优点 : 容易探路且探路与表述合一 ; 缺点 : 表述烦琐且不习惯 , 容易出错 . (4) 实际应用 : 在实 际解题时 , 常常先以分析法为主寻求解题思路 , 再用综合法有条理地表述过程 . 2. 分析法的证题思路 分析法的基本思路是 “ 执果索因 ” . 由求证走向已知 , 即从数学题的待证结论或需要求证的问题出发 , 一步一步探索下去 , 最后寻找到使结论成立的一个明显成立的条件 , 或者是可以证明的条件 . 【 微思考 】 分析法是合情推理还是演绎推理 ? 提示 : 分析法是演绎推理 , 因为分析法的每一步都是严密的逻辑推理 , 因此得到的每一个结论都是正确的 , 不同于合情推理中的 “ 猜想 ” . 【 即时练 】 (2014 · 郑州高二检测 ) 分析法又叫执果索因法 , 若使用分析 法证明 : 设 a>b>c, 且 a+b+c=0, 求证 : 则证明的 依据应是 ( 　　 ) A.a-b>0 B.a-c>0 C.(a-b)(a-c)>0 D.(a-b)(a-c)<0 【 解析 】 选 C. ⇔ b 2 -ac<3a 2 ⇔ (a+c) 2 -ac<3a 2 ⇔ (a-c)(2a+c)>0 ⇔ (a-c)(a-b)>0. 【 题型示范 】 类型一 用分析法证明不等式 【 典例 1】 (1) 已知 a,b 是不相等的正数， 则 x 与 y 的 大小关系为 ______. (2)(2014· 合肥高一检测 ) 已知 a ＞ 0 ，求证： 【 解题探究 】 1. 题 (1) 中 x,y 有何特点 ? 应怎样比较大小 ? 2. 题 (2) 中的不等式能否用基本不等式证明 ? 问题突破的关键点是什么 ? 【 探究提示 】 1.x,y 都是用含有无理式的代数式来表达的 , 可比较 x 2 与 y 2 的大小 ( 因为 x,y 均大于 0). 2. 不能 . 解题的关 键点是利用分析法 , 执果索因 . 【 自主解答 】 (1) 因为 a,b>0, 所以 x>0,y>0. 要比较 x 与 y 的大 小 , 只需比较 x 2 与 y 2 的大小 . 即比较 与 a+b 的大小 , 因为 a,b 为不相等的正数 , 所以 b, 则 x,y 的大小关系为 　　　　 . 【 解题指南 】 将 x,y 平方后比较 x 2 ,y 2 的大小 , 【 解析 】 因为 a ＞ b ＞ 0, 所以 , 所以比较 x 与 y 的大小， 只需比较 x 2 与 y 2 的大小， 即比较 b-2 与 -b 的大小， 由 知， 2 ＞ 2b. 所以 b-2 ＜ -b ，即 x 2 ＜ y 2 , 故 x ＜ y. 答案： x ＜ y 【方法技巧】 分析法证明不等式的方法与技巧 【变式训练】 (2014· 潍坊高二检测 ) 设 a,b 为实数 . 求证： 【证明】 要证 只需证 即证 a 2 +b 2 ≥ (a 2 +b 2 +2ab), 即证 a 2 +b 2 ≥2ab, 由于 a 2 +b 2 ≥2ab 对一切实数恒成立 . 所以 (a+b). 【补偿训练】 已知 a ＞ 6. 求证： 【 证明 】 要证 只需证 即证 即证 只需证 即证 (a-3)(a-6) ＜ (a-5)(a-4) 即证 18 ＜ 20 ， 因为 18 ＜ 20 显然成立， 所以原不等式 类型二 综合法与分析法的综合应用 【典例 2】 (1) 证明函数 f(x)=log 2 ( +x) 是奇函数 . (2)△ABC 的三个内角 A,B,C 成等差数列 ,a,b,c 分别是 A,B,C 所对的边 , 求证 (a+b) -1 +(b+c) -1 =3(a+b+c) -1 . 【解题探究】 1. 题 (1) 中判断函数为奇函数的主要方法是什么 ? 2. 题 (2) 中隐含条件是什么 ? 该怎样应用 ? 【 探究提示 】 1. 利用奇函数的定义即 f(-x)=-f(x). 2. 隐含条件为 B=60°, 利用余弦定理可化得边之间的关系 . 【自主解答】 (1) 因为 >|x|, 所以 +x>0 恒成立 . 所以 f(x)=log 2 ( +x) 的定义域为 R, 所以要证函数 y=log 2 ( +x) 是奇函数 , 只需证 f(-x)=-f(x), 只需证 log 2 ( -x)+log 2 ( +x)=0, 只需证 log 2 [( -x)( +x)]=0, 因为 ( -x)( +x)=x 2 +1-x 2 =1, 而 log 2 1=0 所以上式成立 . 故函数 f(x)=log 2 ( +x) 是奇函数 . (2) 方法一 :( 分析法 ) 要证 (a+b) -1 +(b+c) -1 =3(a+b+c) -1 , 即证 即证 只需证 c(b+c)+a(a+b)=(a+b)(b+c), 只需证 c 2 +a 2 =ac+b 2 , 只需证 b 2 =c 2 +a 2 -2ac · cos60°, 只需证 B=60°. 因为 A,B,C 成等差数列 , 所以 B=60°, 所以 (a+b) -1 +(b+c) -1 =3(a+b+c) -1 . 方法二 :( 综合法 ) 因为△ ABC 的三个内角 A,B,C 成等差数列 , 所以 B=60°. 由余弦定理知 b 2 =c 2 +a 2 -2cacos60°, 得 c 2 +a 2 =ac+b 2 , 两边同时加上 ab+bc 得 c(b+c)+a(a+b)=(a+b)(b+c), 两边同时除以 (a+b)(b+c) 得 所以 (a+b) -1 +(b+c) -1 =3(a+b+c) -1 . 【方法技巧】 1. 分析法与综合法的关系 分析法与综合法的关系可表示为下图 : 从图中可以看出 , 逆向书写分析过程 , 同样可以完成证明 , 这就是综合法 . 由此使我们想到 , 用分析法探路 , 用综合法书写 , 也是一种很好的思维方式 . 2. 分析综合法 分析法与综合法是两种思路相反的推理方法 , 分析法是倒溯 , 综合法是顺推 . 因此常将二者交互使用 , 互补优缺点 , 从而形成分析综合法 , 其证明模式可用框图表示如下 : 其中 P 表示已知条件、定义、定理、公理等 ,Q 表示可证明的结论 . 【变式训练】 已知 00,b>0,a+b=1, 所以 ab≥8 不可能成立 , 而 1=a+b≥2 , 所以 ab≤ . 所以原不等式成立 . 【 规范解答 】 用分析法证明不等式 【 典例 】 (12 分 ) 若已知 n∈N * , 求证 :log (n+1) (n+2)0 时 , 欲证原不等式成立 , 只需证 (ac+bd) 2 ≤(a 2 +b 2 )(c 2 +d 2 ). 即证 a 2 c 2 +2abcd+b 2 d 2 ≤a 2 c 2 +a 2 d 2 +b 2 c 2 +b 2 d 2 , 即证 2abcd≤b 2 c 2 +a 2 d 2 , 即证 0≤(bc-ad) 2 . 因为 a,b,c,d∈R, 所以上式恒成立 . 故原不等式成立 , 综合①②知 , 命题得证 .