2018-2019学年吉林省长春外国语学校高一下学期期末考试数学（文）试题（word版） 6页

长春外国语学校2018-2019学年第二学期期末考试高一年级 数学试卷（文科）‎ 出题人 ： 刘洋 审题人：康乐 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页。考试结束后，将答题卡交回。‎ 注意事项：‎ ‎ 1.答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信 ‎ 息条形码粘贴区。‎ ‎ 2.选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书 ‎ 写，字体工整、笔迹清楚。‎ ‎ 3.请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；‎ ‎ 在草稿纸、试题卷上答题无效。‎ ‎ 4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。‎ ‎5.保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。‎ 第Ⅰ卷 一、选择题：(本题共15小题，每小题4分.在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1.2019°是（ ）‎ A．第一象限角 B．第二象限角 C.第三象限角 D.第四象限角 ‎2.不等式的解集为,则的值为(  )‎ A. B. C. D. ‎ ‎3.已知向量若,则 ( ) A.1 B. C.2 D.3‎ ‎4.函数的最小值为(   ) ‎ A.6    B.7   C.8    D.9‎ ‎5.化简-=（ ）‎ A． B． C． D．‎ ‎6.若，则=（ ）‎ A. - B. C. - D. ‎ ‎7.如图，网格纸上小正方形的边长为，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）‎ A. B. C. D.‎ ‎8.在等比数列中，成等差数列，则公比等于（ ）‎ A. 1或2 B. −1或−2  C. 1或−2  D. −1或2‎ ‎9.在△ABC中，角A、B、C所对的边分别为己知A=60°，则B=（ ）‎ A.45° B.135° C.45°或135° D.以上都不对 ‎10.已知等差数列中，则=（　　）‎ A．10 B． ‎16 C．20 D．24 ‎ ‎11．为了得到函数的图象，可以将函数的图象（　　）‎ A．向左平移个单位长度 B．向右平移个单位长度 ‎ C．向左平移个单位长度 D．向右平移个单位长度 ‎12.在等比数列{an}中，a3＝12，a2＋a4＝30，则a10的值为 (　　)．‎ A．3×10－5 B．3×‎29 C．128 D．3×2－5或3×29‎ ‎13. 若实数x，y满足条件，目标函数，则z 的最大值为(　　)‎ A． B． ‎1 C． 2 D． 0‎ ‎14.设且，则下列不等式成立的是（ ）‎ A. B. C. D. 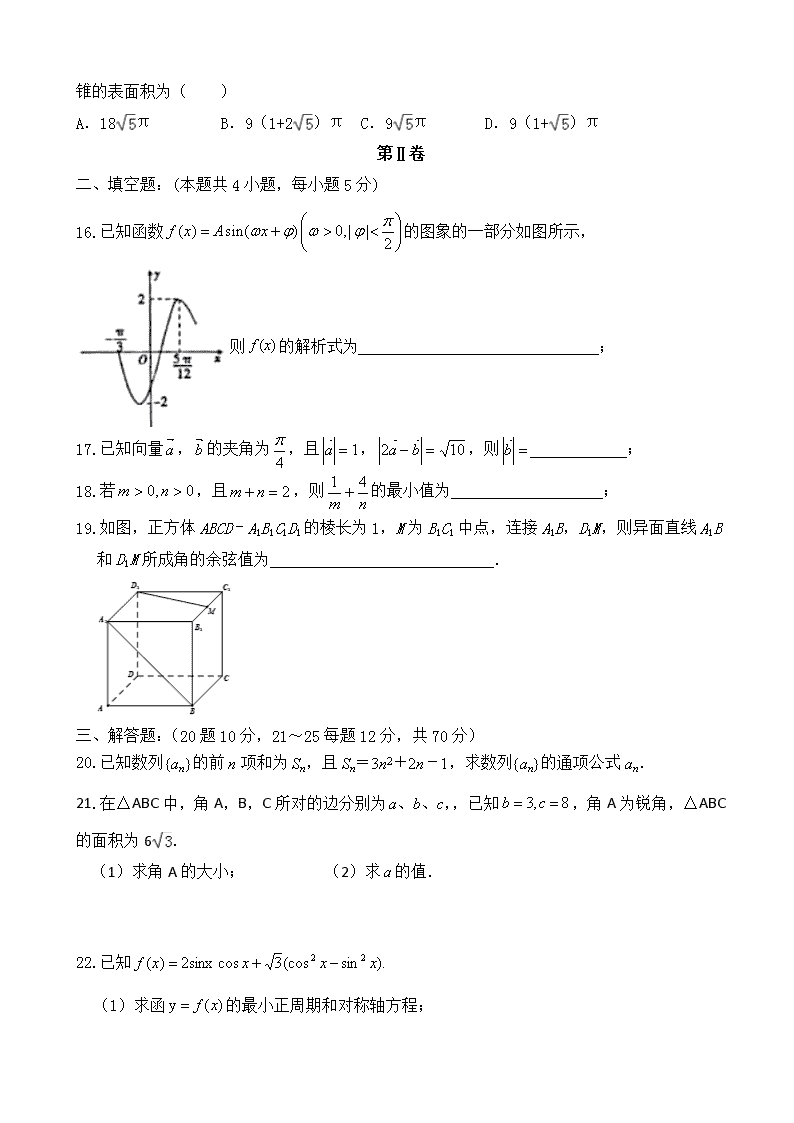‎ ‎15.圆锥的高h和底面半径r之比h：r＝2：1，且圆锥的体积V＝18π，则圆 锥的表面积为（　　）‎ A．18π B．9（1+2）π C．9π D．9（1+）π 第Ⅱ卷 二、填空题：(本题共4小题，每小题5分)‎ ‎16.已知函数的图象的一部分如图所示，‎ 则的解析式为 ；‎ ‎17.已知向量，的夹角为，且，，则 ；‎ ‎18.若，且，则的最小值为 ；‎ ‎19.如图，正方体ABCD﹣A1B‎1C1D1的棱长为1，M为B‎1C1中点，连接A1B，D‎1M，则异面直线A1B和D‎1M所成角的余弦值为　 　．‎ 三、解答题：（20题10分，21～25每题12分，共70分）‎ ‎20.已知数列{an}的前n项和为Sn，且Sn＝3n2＋2n－1，求数列{an}的通项公式an．‎ ‎21.在△ABC中，角A，B，C所对的边分别为，已知，角A为锐角，△ABC的面积为6．‎ ‎（1）求角A的大小； （2）求的值．‎ ‎22.已知 ‎（1）求函的最小正周期和对称轴方程；‎ ‎（2）若∈[0，]，求的值域．‎ ‎23.如图，在四棱锥中，底面是正方形，⊥底面，==2，点是的中点，点是和的交点．‎ ‎(1)证明：∥平面；‎ ‎(2)求三棱锥的体积．‎ ‎24.等差数列中，.‎ ‎(1)求数列的通项公式; ‎ ‎(2)设,求数列的前项和.‎ ‎25.已知，且.‎ ‎(1)若与共线，求的值；‎ ‎(2)设，，若的最大值为，求实数的值.‎ 答案 一、选择题（每题5分，共60分）‎ 1. 2. C 2.B 3.B 4.C5.A 6.B 7.B 8.C 9.A10.C 11.D 12.D13.C 14. A 15.D 二、填空题（每题5分，共20分）‎ ‎16. 17. 18.19.‎ 三、解答题（20题10分，其他每题12分）‎ ‎20.当n＝1时，a1＝S1＝4；当n≥2时，an＝Sn－Sn－1＝3n2＋2n－1－3(n－1)2－2(n－1)＋1＝6n－1，a1＝4不满足上式．∴an＝ ‎21.(1) (2)‎ ‎22.(1)T=, 对称轴 ‎ （2） 值域是 ‎23.(1)略 （2）‎ ‎24(1) （2）‎ ‎25. （1）通过可以算出，‎ 即 ‎（2），设，，，‎ 即的最大值为；‎ ‎①当时，（满足条件）；‎ ‎②当时，‎ ‎（舍）；‎ ‎③当时，（舍）‎ 故答案为