高中数学选修2-2课时练习第一章 章末复习 10页

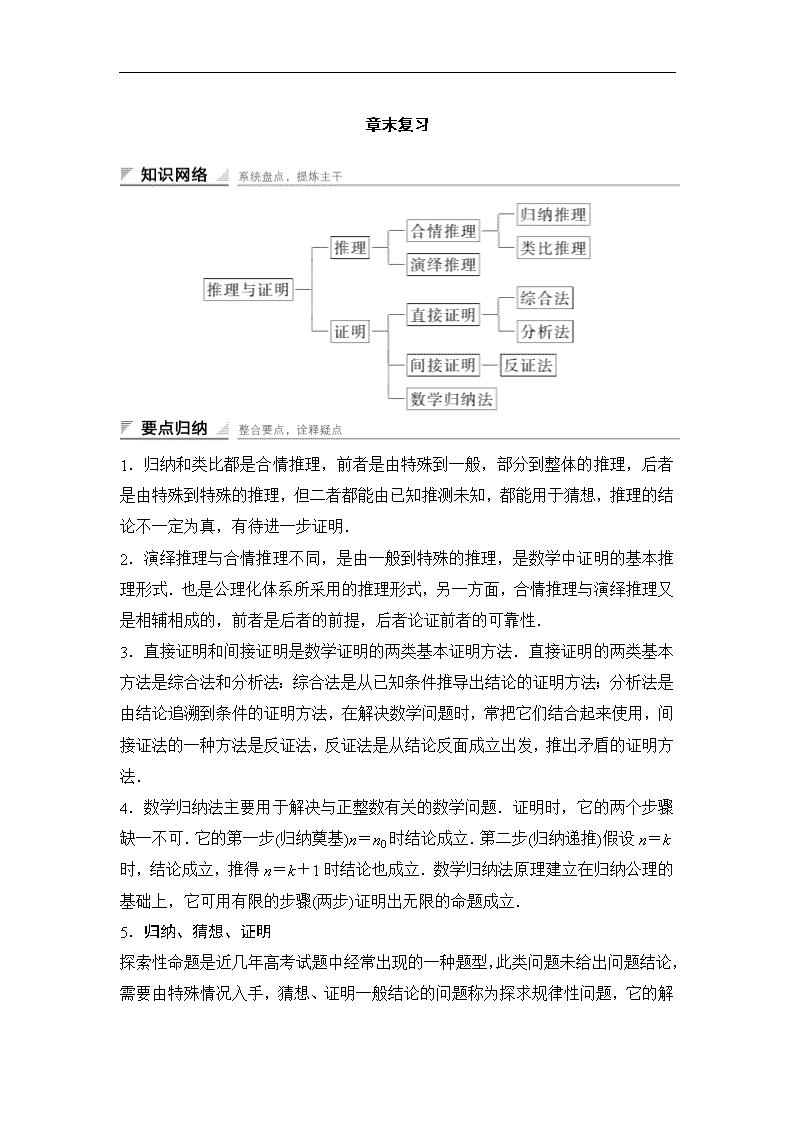
章末复习 1．归纳和类比都是合情推理，前者是由特殊到一般，部分到整体的推理，后者 是由特殊到特殊的推理，但二者都能由已知推测未知，都能用于猜想，推理的结 论不一定为真，有待进一步证明． 2．演绎推理与合情推理不同，是由一般到特殊的推理，是数学中证明的基本推 理形式．也是公理化体系所采用的推理形式，另一方面，合情推理与演绎推理又 是相辅相成的，前者是后者的前提，后者论证前者的可靠性． 3．直接证明和间接证明是数学证明的两类基本证明方法．直接证明的两类基本 方法是综合法和分析法：综合法是从已知条件推导出结论的证明方法；分析法是 由结论追溯到条件的证明方法，在解决数学问题时，常把它们结合起来使用，间 接证法的一种方法是反证法，反证法是从结论反面成立出发，推出矛盾的证明方 法． 4．数学归纳法主要用于解决与正整数有关的数学问题．证明时，它的两个步骤 缺一不可．它的第一步(归纳奠基)n＝n0 时结论成立．第二步(归纳递推)假设 n＝k 时，结论成立，推得 n＝k＋1 时结论也成立．数学归纳法原理建立在归纳公理的 基础上，它可用有限的步骤(两步)证明出无限的命题成立． 5．归纳、猜想、证明 探索性命题是近几年高考试题中经常出现的一种题型，此类问题未给出问题结论， 需要由特殊情况入手，猜想、证明一般结论的问题称为探求规律性问题，它的解 题思想是：从给出的条件出发，通过观察、试验、归纳、猜想，探索出结论，然 后再对归纳、猜想的结论进行证明． 题型一　归纳推理和类比推理 归纳推理和类比推理是常用的合情推理，两种推理的结论“合情”但不一定“合 理”，其正确性都有待严格证明．尽管如此，合情推理在探索新知识方面有着极 其重要的作用． 运用合情推理时，要认识到观察、归纳、类比、猜想、证明是相互联系的．在解 决问题时，可以先从观察入手，发现问题的特点，形成解决问题的初步思路，然 后用归纳、类比的方法进行探索、猜想，最后用逻辑推理方法进行验证．　　　　　　　　　　　　　　　　　　　 例 1　观察下列各式：a＋b＝1，a 2＋b2＝3，a3＋b3＝4，a4＋b4＝7，a5＋b5＝ 11，…，则 a10＋b10＝(　　) A．28 B．76 C．123 D．199 答案　C 解析　记 an＋bn＝f(n)， 则 f(3)＝f(1)＋f(2)＝1＋3＝4； f(4)＝f(2)＋f(3)＝3＋4＝7； f(5)＝f(3)＋f(4)＝11. 通过观察不难发现 f(n)＝f(n－1)＋f(n－2)(n∈N＋，n≥3)， 则 f(6)＝f(4)＋f(5)＝18； f(7)＝f(5)＋f(6)＝29； f(8)＝f(6)＋f(7)＝47； f(9)＝f(7)＋f(8)＝76； f(10)＝f(8)＋f(9)＝123. 所以 a10＋b10＝123. 跟踪演练 1　自然数按下表的规律排列 则上起第 2 007 行，左起第 2 008 列的数为(　　)　　　　　　　　　　　　　　　　　　　 A．2 0072 B．2 0082 C．2 006×2 007 D．2 007×2 008 答案　D 解析　经观察可得这个自然数表的排列特点： ①第一列的每个数都是完全平方数，并且恰好等于它所在行数的平方，即第 n 行 的第 1 个数为 n2； ②第一行第 n 个数为(n－1)2＋1； ③第 n 行从第 1 个数至第 n 个数依次递减 1； ④第 n 列从第 1 个数至第 n 个数依次递增 1. 故上起第 2 007 行，左起第 2 008 列的数，应是第 2 008 列的第 2 007 个数，即为 [(2 008－1)2＋1]＋2 006＝2 007×2 008. 题型二　直接证明 由近三年的高考题可以看出，直接证明的考查中，各种题型均有体现，尤其是解 答题，近几年来一直是考查证明方法的热点与重点． 综合法和分析法是直接证明中最基本的两种证明方法，也是解决数学问题常用的 思维方式．如果从解题的切入点的角度细分，直接证明方法可具体分为：比较法、 代换法、放缩法、判别式法、构造函数法等，应用综合法证明问题时，必须首先 想到从哪里开始起步，分析法就可以帮助我们克服这种困难，在实际证明问题时， 应当把分析法和综合法结合起来使用． 例 2　已知 a>0，求证： a2＋ 1 a2 － 2≥a＋1 a －2. 证明　要证 a2＋ 1 a2 － 2≥a＋1 a －2， 只需证 a2＋ 1 a2 ＋2≥a＋1 a ＋ 2. ∵a>0，故只需证 ( a2＋ 1 a2＋2)2≥(a＋1 a ＋ 2)2， 即 a2＋ 1 a2 ＋4 a2＋ 1 a2 ＋4≥a2＋2＋ 1 a2 ＋ 2 2(a＋1 a)＋2， 从而只需证 2 a2＋ 1 a2 ≥ 2(a＋1 a)， 只要证 4(a2＋ 1 a2)≥2(a2＋2＋ 1 a2)， 即 a2＋ 1 a2 ≥2，而上述不等式显然成立，故原不等式成立． 跟踪演练 2　如图，在四面体 B－ACD 中，CB＝CD，AD⊥BD，且 E，F 分别是 AB，BD 的中点，求证： (1)直线 EF∥平面 ACD； (2)平面 EFC⊥平面 BCD. 证明　(1)要证直线 EF∥平面 ACD， 只需证 EF∥AD 且 EF⊄平面 ACD. 因为 E，F 分别是 AB，BD 的中点， 所以 EF 是△ABD 的中位线， 所以 EF∥AD， 所以直线 EF∥平面 ACD. (2)要证平面 EFC⊥平面 BCD， 只需证 BD⊥平面 EFC， 只需证Error! 因为Error!所以 EF⊥BD. 又因为 CB＝CD，F 为 BD 的中点， 所以 CF⊥BD.所以平面 EFC⊥平面 BCD. 题型三　反证法 如果一个命题的结论难以直接证明时，可以考虑反证法．通过反设结论，经过逻 辑推理，得出矛盾，从而肯定原结论成立． 反证法是高中数学的一种重要的证明方法，在不等式和立体几何的证明中经常用 到，在高考题中也经常体现，它所反映出的“正难则反”的解决问题的思想方法 更为重要．反证法主要证明：否定性、唯一性命题；至多、至少型问题；几何问 题． 例 3　如图所示，已知两个正方形 ABCD 和 DCEF 不在同一平面内，M，N 分别 为 AB、DF 的中点． (1)若平面 ABCD⊥平面 DCEF，求直线 MN 与平面 DCEF 所成角的正弦值； (2)用反证法证明：直线 ME 与 BN 是两条异面直线． (1)解　法一　如图(1)所示，取 CD 的中点 G，连接 MG，NG，设正方形 ABCD， DCEF 的边长为 2， 图(1) 则 MG⊥CD，MG＝2，NG＝ 2， ∵平面 ABCD⊥平面 DCEF， ∴MG⊥平面 DCEF， ∴∠MNG 是 MN 与平面 DCEF 所成的角． ∵MN＝ 6，∴sin∠MNG＝ 6 3 ， ∴直线 MN 与平面 DCEF 所成角的正弦值为 6 3 . 法二　设正方形 ABCD，DCEF 的边长为 2，以 D 为坐标原点，分别以射线 DC， DF，DA 为 x，y，z 轴正半轴建立空间直角坐标系，如图(2)所示． 图(2) 则 M(1,0,2)，N(0,1,0)， ∴MN→ ＝(－1,1，－2)． 又DA→ ＝(0,0,2)为平面 DCEF 的法向量， ∴cos〈MN→ ，DA→ 〉＝ MN→ ·DA→ |MN→ ||DA→ | ＝－ 6 3 ， ∴MN 与平面 DCEF 所成角的正弦值为 |cos〈MN→ ，DA→ 〉|＝ 6 3 . (2)证明　假设直线 ME 与 BN 共面，则 AB⊂平面 MBEN，且平面 MBEN 与平面 DCEF 交于 EN， ∵两正方形不共面， ∴AB⊄平面 DCEF. 又 AB∥CD，所以 AB∥平面 DCEF，而 EN 为平面 MBEN 与平面 DCEF 的交线， ∴AB∥EN.又 AB∥CD∥EF， ∴EN∥EF，这与 EN∩EF＝E 矛盾，故假设不成立． ∴ME 与 BN 不共面，即它们是异面直线． 跟踪演练 3　若 a，b，c 均为实数，且 a＝x2－2y＋π 2 ，b＝y2－2z＋π 3 ，c＝z2－2x＋ π 6.求证：a，b，c 中至少有一个大于 0. 证明　假设 a，b，c 都不大于 0，即 a≤0，b≤0，c≤0， 则 a＋b＋c≤0，而 a＋b＋c＝x2－2y＋π 2 ＋y2－2z＋π 3 ＋z2－2x＋π 6 ＝(x－1)2＋(y－1)2 ＋(z－1)2＋π－3. ∵π－3＞0，且(x－1)2＋(y－1)2＋(z－1)2≥0， ∴a＋b＋c＞0， 这与 a＋b＋c≤0 矛盾，因此假设不成立，∴a，b，c 中至少有一个大于 0. 题型四　数学归纳法 1．数学归纳法事实上是一种完全归纳的证明方法，它适用于与自然数有关的问 题．两个步骤、一个结论缺一不可，否则结论不成立；在证明递推步骤时，必须 使用归纳假设，必须进行恒等变换． 2．探索性命题是近几年高考试题中经常出现的一种题型，此类问题未给出问题 的结论，需要由特殊情况入手，猜想、证明一般结论，它的解题思路是：从给出 条件出发，通过观察、试验、归纳、猜想、探索出结论，然后再对归纳，猜想的 结论进行证明． 例 4　等比数列{an}的前 n 项和为 Sn，已知对任意的 n∈N＋，点(n，Sn)均在函数 y＝bx＋r(b＞0 且 b≠1，b，r 均为常数)的图像上． (1)求 r 的值； (2)当 b＝2 时，记 bn＝2(log2an＋1)(n∈N＋)， 证明：对任意的 n∈N＋，不等式b1＋1 b1 ·b2＋1 b2 ·…· bn＋1 bn ＞ n＋1成立． (1)解　由题意：Sn＝bn＋r， 当 n≥2 时，Sn－1＝bn－1＋r， 所以 an＝Sn－Sn－1＝bn－1(b－1)， 由于 b＞0 且 b≠1， 所以 n≥2 时，{an}是以 b 为公比的等比数列． 又 a1＝b＋r，a2＝b(b－1)， a2 a1 ＝b，即b(b－1) b＋r ＝b，解得 r＝－1. (2)证明　当 b＝2 时，由(1)知 an＝2n－1， 因此 bn＝2n(n∈N＋)， 所证不等式为2＋1 2 ·4＋1 4 ·…· 2n＋1 2n ＞ n＋1. ①当 n＝1 时，左式＝3 2 ，右式＝ 2. 左式＞右式，所以结论成立． ②假设 n＝k(k∈N＋)时结论成立， 即2＋1 2 ·4＋1 4 ·…· 2k＋1 2k ＞ k＋1， 则当 n＝k＋1 时，2＋1 2 ·4＋1 4 ·…· 2k＋1 2k · 2k＋3 2(k＋1) ＞ k＋1· 2k＋3 2(k＋1)＝ 2k＋3 2 k＋1 . 要证当 n＝k＋1 时结论成立， 只需证 2k＋3 2 k＋1 ＞ k＋2成立， 只需证：4k2＋12k＋9＞4k2＋12k＋8 成立，显然成立， ∴当 n＝k＋1 时，2＋1 2 ·4＋1 4 ·…· 2k＋1 2k · 2k＋3 2(k＋1)＞ (k＋1)＋1成立，综合①②可知 不等式b1＋1 b1 ·b2＋1 b2 ·…· bn＋1 bn ＞ n＋1成立． 跟踪演练 4　数列{an}满足：a1＝1，an＋1＝1 2an＋1. (1)写出 a2，a3，a4. (2)求数列{an}的通项公式． 解　(1)因为 a1＝1，an＋1＝1 2an＋1， 所以 a2＝1 2a1＋1＝1 2 ＋1＝3 2 ， a3＝1 2a2＋1＝1 2·3 2 ＋1＝7 4 ， a4＝1 2a3＋1＝1 2·7 4 ＋1＝15 8 . (2)解　法一　猜想 an＝2n－1 2n－1 ，下面用数学归纳法证明． 证明　(1)当 n＝1 时，a1＝21－1 21－1 ＝1，满足上式，显然成立； (2)假设当 n＝k 时 ak＝2k－1 2k－1 ，那么当 n＝k＋1 时， ak＋1＝1 2ak＋1＝1 2·2k－1 2k－1 ＋1＝2k－1 2k ＋1＝2k－1＋2k 2k ＝2k＋1－1 2k 满足上式，即当 n＝k ＋1 时猜想也成立． 由(1)(2)可知，对于 n∈N＋都有 an＝2n－1 2n－1 . 法二　因为 an＋1＝1 2an＋1， 所以 an＋1－2＝1 2an＋1－2， 即 an＋1－2＝1 2(an－2)， 设 bn＝an－2，则 bn＋1＝1 2bn，即{bn}是以－1 为首项，1 2 为公比的等比数列， 所以 bn＝b1·qn－1＝－ 1 2n－1 ， 所以 an＝bn＋2＝2n－1 2n－1 . 1．合情推理主要包括归纳推理和类比推理 (1)归纳推理的基本模式：a，b，c∈M 且 a，b，c 具有某属性，结论∀d∈M，d 也具有某属性． (2)类比推理的基本模式：A 具有属性 a，b，c，d；B 具有属性 a′，b′，c′； 结论：B 具有属性 d′.(a，b，c，d 与 a′，b′，c′，d′相似或相同)． 2．使用反证法证明问题时，常见的“结论词”与“反设词”列表如下： 原结论词 反设词 原结论词 反设词 至少有 一个 一个也没有 对所有 x 成立 存在某个 x 不成立 至多有一个 至少有两个 对任意 x 不成立 存在某个 x 成立 至少有 n 个 至多有 n－1 个 p 或 q 綈 p 且綈 q 至多有 n 个 至少有 n＋1 个 p 且 q 綈 p 或綈 q 3.数学归纳法的应用必须注意以下两点： (1)验证是基础：数学归纳法的原理表明：第一个步骤是要找一个数 n0，这个数 n0 就是要证明的命题对象的最小自然数，这个自然数并不一定都是“1”． (2)递推是关键：数学归纳法的实质在于递推，所以从“k”到“k＋1”的过程，必 须把归纳假设“n＝k”作为条件来导出“n＝k＋1”时的命题，在推导过程中， 要把归纳假设用一次或几次．