高中数学人教a版选修4-1配套课件：2_5 与圆有关的比例线段 30页

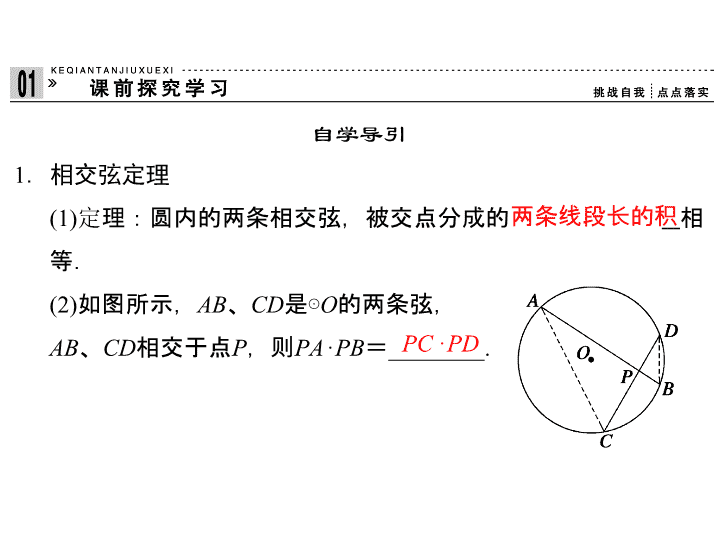
第 5 课时　与圆有关的比例线段 【 课标要求 】 1 ． 经 历相交弦定理、割线定理、切割线定理、切线长定理的探究过程，体会运动变化思想，认识四条定理的内在联系． 2 ．理解相交弦定理、割线定理、切割线定理、切线长定理，能应用四条定理解决相关的几何问题． 3 ．通过探究，进一步体会运动变化思想，体验数学探究的过程． 【 核心扫描 】 1 ． 理 解相交弦定理、割线定理、切割线定理及切线长定理． ( 重点 ) 2 ． 运 用这些定理解决相关的几何问题． ( 难点 ) 自学导引 1 ． 相交弦定理 (1) 定 理：圆内的两条相交弦，被交点分成的 相等． (2) 如图所示， AB 、 CD 是 ⊙ O 的两条弦， AB 、 CD 相交于点 P ，则 PA · PB ＝ ________. 两条线段长的积 PC · PD 2 ．割线定理 (1) 定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的 _____ 相等． (2) 如果 PA 和 PC 是圆的两条割线，与圆分别交于点 B 、 A 和 D 、 C ，则 PA · PB ＝ _________. 积 PC · PD 3 ．切割线定理 (1) 切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的 ___________ ． (2) 如图所示， PBA 是 ⊙ O 的割线， PC 是 ⊙ O 的切线，则 PC 2 ＝ __________. 比例中项 PA · PB 4 ．切线长定理 (1) 切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的 _______ ． (2) 如图所示， PA 、 PC 是 ⊙ O 的切线，则有 PA ＝ ______. 夹角 PC 名师点睛 1 ． 相 交弦定理的证明过程是利用了分类讨论思想进行分析的，也可以理解为由特殊到一般的过程进行分析的． 2 ．割线定理是圆中的比例线段，在证明割线定理时所用的构造相似三角形的方法十分重要，应注意很好地把握． 3 ．要真正弄懂切割线定理的数量关系，把握定理叙述中的 “ 从 ” 、 “ 引 ” 、 “ 切线长 ” 、 “ 两条线段长 ” 等关键字样． 4 ． (1) 切线长定理在证明线段相等、角相等及垂直关系中占有重要地位，故为重点． (2) “ 切割线定理 ” 和 “ 切线长定理 ” 实际上是割线定理的特例． (3) 深刻理解结论：由于圆是轴对称图形，在图中若再连接 AB 与 OP 交于点 C ，则存在射影定理的基本图形，于是有 AC 2 ＝ BC 2 ＝ PC · OC ， PA 2 ＝ PB 2 ＝ PC · PO ， AO 2 ＝ BO 2 ＝ OC · OP . 题型一　相交弦定理的应用 【 例 1】 在 半径为 12 cm 的圆中，垂直平分半径的弦的长为 ( 　　 ) ．　　　　　　　　　　　　　　　　　　 A ． 3 cm B ． 27 cm C ． 12 cm D ． 6 cm [ 思维启迪 ] 准确使用相交弦定理解决此题． 答案　 C 反思感悟　 用相交弦定理解决此类问题步骤： ① 结合图形，找准分点及线段被分点所分成的线段； ② 正确应用相交弦定理列出关系式； ③ 代入数值运算，求出正确的答案． 【 变式 1】 如图 所示，已知 AP ＝ 3 cm ， PB ＝ 5 cm ， CP ＝ 2.5 cm ，求 CD . 解　 由相交弦定理，得 PA · PB ＝ PC · PD . 将 PA ＝ 3 cm ， PB ＝ 5 cm 代入上式，得 PD ＝ 6 cm. 所以 CD ＝ CP ＋ PD ＝ 6 ＋ 2.5 ＝ 8.5(cm) ． 题型二　切割线定理的应用 【 例 2】 如 图， AD 为 ⊙ O 的直径， AB 为 ⊙ O 的切线，割线 BMN 交 AD 的延长线于 C ，且 BM ＝ MN ＝ NC ， 若 AB ＝ 2. 求 : (1) BC 的长； (2) ⊙ O 的半径 r . 反思感悟　 (1) 应用切割线定理的一般步骤： ① 观察图形，寻找切割线定理成立的条件； ② 找准相关线段的长度，列出等式； ③ 解方程，求出结果． (2) 应用切割线定理及割线定理的前提条件： 只有从圆外一点才可能产生割线定理或切割线定理，切割线定理是指一条切线和一条割线，而割线定理则是指两条割线，只有弄清前提，才能正确运用定理． 【 变式 2】 如图 ，已知 Rt △ ABC 的两条直角边 AC 、 BC 的长分别为 3 cm 、 4 cm ，以 AC 为直径作圆与斜边 AB 交于点 D ，求 BD 的长． 题型三　切线长定理的应用 【 例 3】 如图 所示， P 为⊙ O 外一点， PA 、 PB 分别切 ⊙ O 于点 A 、 B ，点 C 为 AB 上任意一点，过 C 作 ⊙ O 的切线，分别交 PA 、 PB 于点 D 、 E ， △ PDE 的周长为 8 cm ，且 ∠ DOE ＝ 70° ， 求 (1) PA 的长； (2) ∠ P 的度数． [ 思维启迪 ] 利用切线长定理解决此题． 解　 (1) PA ＝ PD ＋ DA ， PB ＝ PE ＋ EB ， DE ＝ DC ＋ CE . 由“ 切 线长定理”可知 PA ＝ PB ， DA ＝ DC ， EB ＝ EC . 所以 PA ＋ PB ＝ 2 PA ＝ PD ＋ PE ＋ DA ＋ EB ＝ PD ＋ PE ＋ ( DC ＋ EC ) ，即 2 PA ＝ PD ＋ PE ＋ DE . 而△ PDE 的周长＝ PD ＋ PE ＋ DE ＝ 8 cm. 所以 2 PA ＝ 8 cm ， PA ＝ 4 cm. (2) 连接 OA 、 OB 、 OC ，则 PA ⊥ OA ， PB ⊥ OB ， DE ⊥ OC ， 且 ∠ 1 ＝ ∠ 2 ， ∠ 3 ＝ ∠ 4 ＝ ∠ 9 ＝ 90°. 由三角形内角和得 ∠ 5 ＝ ∠ 6 ， ∠ 7 ＝ ∠ 8. 又 ∠ P ＋ ∠ PAO ＋ ∠ AOB ＋ ∠ PBO ＝ 360° ，所以 ∠ P ＝ 180° － ( ∠ 5 ＋ ∠ 6 ＋ ∠ 7 ＋ ∠ 8) ．由已知 ∠ 6 ＋ ∠ 7 ＝ 70° ，所以 ∠ 5 ＋ ∠ 6 ＋ ∠ 7 ＋ ∠ 8 ＝ 140° ，所以 ∠ P ＝ 180° － 140° ＝ 40°. 反思感悟　 切线上一点到切点的距离为切线长，并且这点与圆心的连线平分两条切线的夹角．解此题第 (2) 问时，注意四边形内角和这一隐含条件的使用，当已知条件中有切线时，通常连结切点和圆心，以便使用 “ 垂直 ” 这一结论，这也是切线问题常用的辅助线． 【 变式 3】 如图 ， ⊙ O 为 △ ABC 的内切圆， AC 、 BC 、 AB 分别与 ⊙ O 切于点 D 、 E 、 F ， ∠ C ＝ 90° ， AD ＝ 3 ， ⊙ O 的半径为 2 ，则 BC ＝ ________. 解析　 如图所示，分别连接 OD ， OE 、 OF . ∵ OE ＝ OD ， CD ＝ CE ， OE ⊥ BC ， OD ⊥ AC ， ∴ 四边形 OECD 是正方形． 设 BF ＝ x ，则 BE ＝ x . ∵ AD ＝ AF ＝ 3 ， CD ＝ CE ＝ 2 ， ∴ (2 ＋ x ) 2 ＋ 25 ＝ ( x ＋ 3) 2 ，解得 x ＝ 10 ， ∴ BC ＝ 12. 答案　 12 高考在线　与圆有关的比例线段的考查 考点点击　 高考题在这部分可能与圆的切线、以及其他知识综合出现，以前在中考中此部分是考查的重点，现在放在高中部分，虽不是高考的重点，但有可能出现在选择题、填空题中，且难度较小． 【 考题 1】 (2012 · 北京高考 ) 如图， ∠ ACB ＝ 90° ， CD ⊥ AB 于点 D ，以 BD 为直径的圆与 BC 交于点 E ，则 ( 　　 ) ． A ． CE · CB ＝ AD · DB B ． CE · CB ＝ AD · AB C ． AD · AB ＝ CD 2 D ． CE · EB ＝ CD 2 解析　 ∵ CD ⊥ AB ， ∴ 以 BD 为直径的圆与 CD 相切． ∴ CD 2 ＝ CE · CB . 在 Rt △ ABC 中， CD 为斜边 AB 上的高，有 CD 2 ＝ AD · DB ，因此， CE · CB ＝ AD · DB . 答案　 A 反思感悟 　本题考查直角三角形射影定理．切割线定理等基础知识，考查推理论证能力． 反思感悟　 本小题主要考查解直角三角形知识及相交弦定理的应用． 【 考题 3】 (2010 · 陕西高考 ) 如图，已知 Rt △ ABC 的两条直角边 AC ， BC 的长分别为 3 cm ， 4 cm ，以 AC 为直径的圆与 AB 交于点 D ，则＝ ________.