2021届课标版高考理科数学大一轮复习课件：6-1　数列的概念及表示（讲解部分） 14页

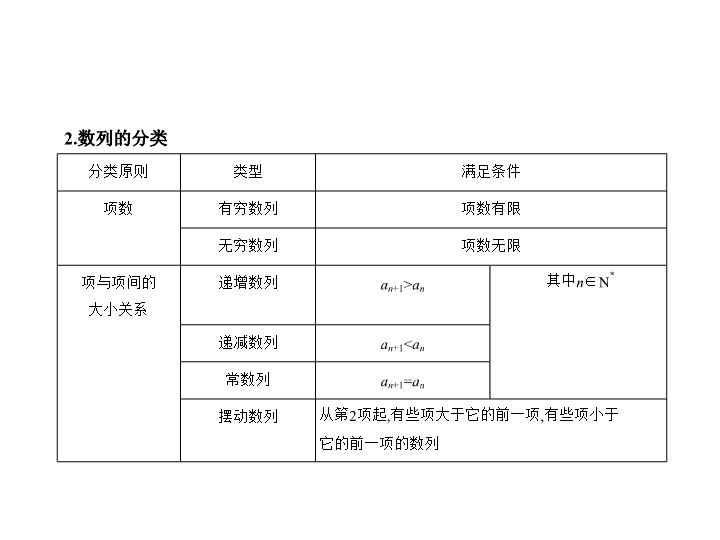
专题六　数　列 6.1 　数列的概念及表示 高考理数 考点    数列的概念及表示方法 考点清单 考向基础 1.数列的概念 (1)数列的定义:按照 一定顺序 排列的一列数称为数列,数列中的每一个数 叫做这个数列的项. (2)数列与函数的关系:从函数观点看,数列可以看成以正整数集N * (或它的 有限子集{1,2, … , n })为 定义域 的函数 a n = f ( n )当自变量按照从小到大的顺序 依次取值时所对应的一列函数值. 分类原则 类型 满足条件 项数 有穷数列 项数有限 无穷数列 项数无限 项与项间的 大小关系 递增数列 a n +1 > a n 其中 n ∈N * 递减数列 a n +1 < a n 常数列 a n +1 = a n 摆动数列 从第2项起,有些项大于它的前一项,有些项小于 它的前一项的数列 2.数列的分类 3.数列常用的两种表示方法 (1)通项公式:如果数列{ a n }的第 n 项与 序号 n 之间的关系可以用一个式子来 表示,那么这个式子叫做这个数列的通项公式. (2)递推公式:如果已知数列{ a n }的第1项(或前几项),且从第二项(或某一项) 开始的任一项与它的前一项(或前几项)间的关系可以用一个式子来表示, 那么这个式子就叫做这个数列的递推公式. 4.已知数列{ a n }的前 n 项和为 S n ,则 (1) S n = a 1 + a 2 + … + a n ; (2) a n =   考向突破 考向一    求数列的通项公式 例1     (2019河南焦作第四次模拟,14)已知数列{ a n }的通项公式为 a n =2 n ,记数 列{ a n b n }的前 n 项和为 S n ,若   +1= n ,则数列{ b n }的通项公式为 b n = 　　　     . 解析　 因为   +1= n ,所以 S n =( n -1)·2 n +1 +2.所以当 n ≥ 2时, S n -1 =( n -2)2 n +2,两式 相减,得 a n b n = n ·2 n ,所以 b n = n ;当 n =1时, a 1 b 1 =2,所以 b 1 =1.综上所述, b n = n , n ∈N * . 故答案为 n . 答案      n 考向二    数列的性质 例2     (2019江西宜春期末,9)已知函数 f ( x )=   若数列{ a n }满足 a 1 =   , a n +1 = f ( a n )( n ∈N * ),则 a 2 019 =   (　　) A.   　　　　    B.   　　　　     C.   　　　　    D.   解析 　由题意,知 a 2 = f   =   , a 3 = f   =   , a 4 = f   =   , a 5 = f   =   , a 6 = f   =   , a 7 = f   =   , …… ,故数列{ a n }从第三项起构成周期数列,且周期为3,故 a 2 019 = a 3 =   .故选D. 答案     D 方法1      利用Sn与an的关系求通项公式 已知 S n 求 a n 的三个步骤: (1)先利用 a 1 = S 1 求出 a 1 . (2)用 n -1替换 S n 中的 n 得到一个新的关系,利用 a n = S n - S n -1 ( n ≥ 2)便可求出当 n ≥ 2时 a n 的表达式. (3)对 n =1时的结果进行检验,看是否符合 n ≥ 2时 a n 的表达式,若符合,则可以 把数列的通项公式合写;若不符合,则应该分 n =1与 n ≥ 2两段来写. 方法技巧 例1     (2019湖南衡阳高中毕业班联考(二),16)已知数列{ a n }, a 1 =2, S n 为数列 { a n }的前 n 项和,且对任意 n ≥ 2,都有   =1,则{ a n }的通项公式为 　　     　　　　　     . 解析      n ≥ 2时,由   =1 ⇒   =   =1 ⇒   -   =   . 又   =   =   ,∴   是以   为首项,   为公差的等差数列.∴   =   ,∴ S n =   ,当 n ≥ 2时, a n = S n - S n -1 =   -   =-   ,所以 a n =   答案      a n =   方法2      由递推关系求数列的通项公式 方法 解读 适合题型 叠加法 对于形如 a n +1 - a n = f ( n )的数列的递推关系式,若 f (1)+ f (2)+ … + f ( n )的和是可求的,可用多项式相加法求得 a n ,也称这种方法为叠加法 a n +1 - a n = f ( n )型 叠乘法 对于形如   = f ( n )的数列的递推关系式,若 f (1)· f (2)· … · f ( n )的积是可求的,则可用多项式相乘法求得 a n ,也称这种方法为叠乘法   = f ( n )型 构造法 形如 a n +1 = pa n + q (其中 p , q 均为常数, pq ( p -1) ≠ 0)的递推关系 式,把原递推关系式转化为 a n +1 - t = p ( a n - t ),其中 t =   ,然后构造   = p ,即{ a n - t }是以 a 1 - t 为首项, p 为公比的等比数列 a n +1 = pa n + q 型 辅助数列法 形如 a n +1 = pa n + q n (其中 p , q 均为常数, pq ( p -1) ≠ 0)的递推关系式, 要先在递推关系式两边同除以 q n +1 ,得   =   ·   +   ,引入辅助数列{ b n }   ,得 b n +1 =   · b n +   ,再用构造法解决 a n +1 = pa n + q n 型 取倒数法 对 a n =   (其中 mkb ≠ 0)取倒数,得到   =   ·   ⇔   =   ·   +   .令 b n =   ,则{ b n }可归为 a n +1 = pa n + q ( p ≠ 0,1, q ≠ 0)型 a n =   ( mkb ≠ 0)型 取对数法 对 a n = p   两边同取常用对数,得lg a n = r lg a n -1 +lg p ,令 b n =lg a n ,则{ b n }可归为 a n +1 = pa n + q ( p ≠ 0,1, q ≠ 0)型 a n = p   ( n ≥ 2, p >0, p ≠ 1)型 例2     (2019河北省级示范性高中4月联考,15)数列{ a n }满足 a 1 =3,且对于任 意的 n ∈N * 都有 a n +1 - a n = n +2,则 a 39 = 　　　     . 解析 　因为 a n +1 - a n = n +2,所以 a 2 - a 1 =3, a 3 - a 2 =4, a 4 - a 3 =5, …… , a n - a n -1 = n +1( n ≥ 2),上面( n -1)个式子左右两边分别相加 得 a n - a 1 =   ( n ≥ 2),即 a n =   ( n ≥ 2),当 n =1时, a 1 =3适合上式,所 以 a n =   , n ∈N * ,所以 a 39 =   =820. 答案 　820 方法3      数列的单调性和最大(小)项 1.用作差比较法,根据 a n +1 - a n 的符号判断数列{ a n }是递增数列、递减数列或 常数列. 2.用作商比较法,根据   ( a n >0或 a n <0)与1的大小关系进行判断. 3.结合相应函数的图象直观判断. 例3     (2019河南开封一模,16)已知数列{ a n }的前 n 项和为 S n ,数列{ b n }的前 n 项和为 T n .满足 a 1 =2,3 S n =( n + m ) a n ( m ∈R),且 a n b n = n ,若存在 n ∈N * ,使得 λ + T n ≥ T 2 n 成立,则实数 λ 的最小值为 　　　     . 解析 　∵3 S n =( n + m ) a n ,∴3 S 1 =3 a 1 =(1+ m ) a 1 ,解得 m =2,∴3 S n =( n +2) a n ①,当 n ≥ 2 时,3 S n -1 =( n +1) a n -1 ②,由①-②可得3 a n =( n +2) a n -( n +1) a n -1 ,即( n -1) a n =( n +1) a n -1 , ∴   =   ,∴   =   ,   =   ,   =   , …… ,   =   ,   =   ,累乘可得 a n = n ( n +1) ( n ≥ 2),经检验, a 1 =2符合上式,∴ a n = n ( n +1), n ∈N * .∵ a n b n = n ,∴ b n =   ,令 B n = T 2 n - T n =   +   + … +   ,则 B n +1 - B n =   >0,∴数列{ B n }为 递增数列,∴ B n ≥ B 1 =   .∵存在 n ∈N * ,使得 λ + T n ≥ T 2 n 成立,∴ λ ≥ B 1 =   ,故实数 λ 的最小值为   . 答案