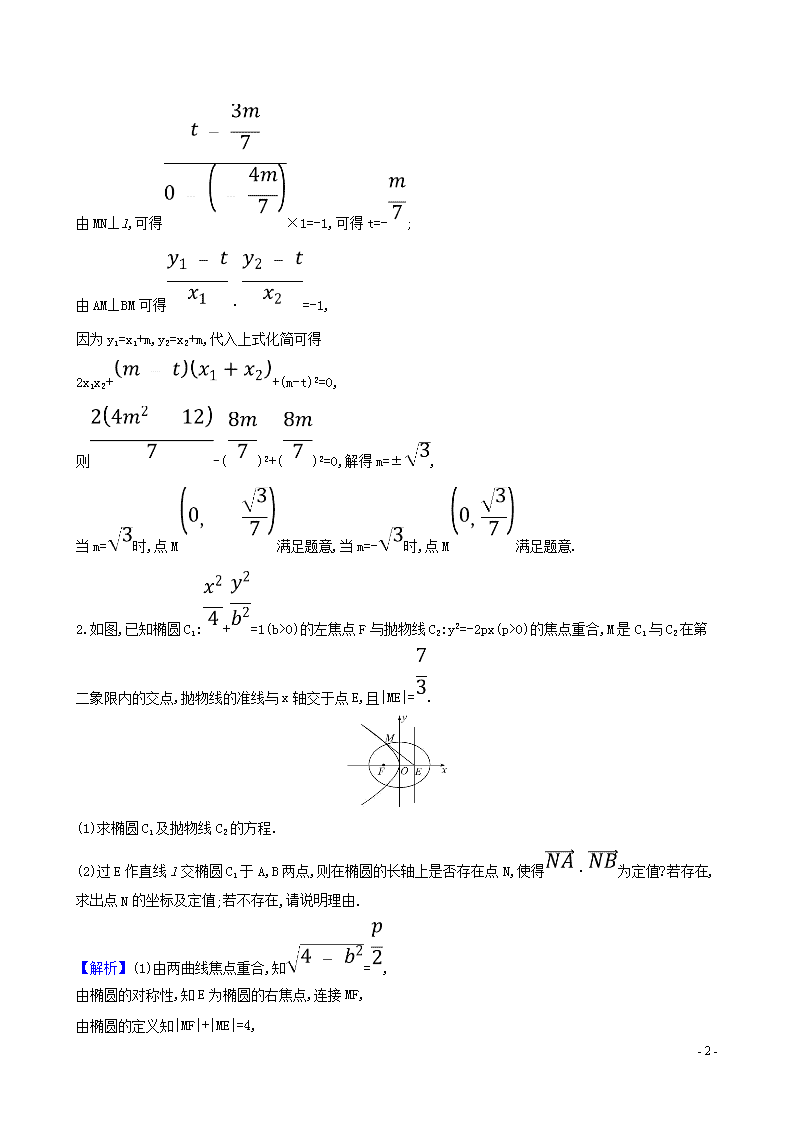2021版高考数学一轮复习核心素养测评六十五圆锥曲线与其他知识的交汇问题理北师大版 4页

- 1 - 核心素养测评六十五 圆锥曲线与其他知识的交汇问题 1. 已知椭圆 C: + =1(a>b>0)的一个焦点为 F(1,0),点 P 在 C 上. (1)求椭圆 C 的方程. (2)若直线 l:y=x+m 与椭圆 C 相交于 A,B 两点,问 y 轴上是否存在点 M,使得△ABM 是以 M 为直角顶点的等腰 直角三角形?若存在,求点 M 的坐标;若不存在,说明理由. 【解析】(1)由题意可得 c=1,点 P 在 C 上,所以 + =1,又 a2=b2+c2=b2+1, 解得 a2=4,b2=3,所以椭圆 C 的方程为 + =1. (2)假设 y 轴上存在点 M ,使△ABM 是以 M 为直角顶点的等腰直角三角形, 设 A ,B ,线段 AB 的中点为 N ,由 ,消去 y 可得 7x2+8mx+4m2-12=0, Δ=64m2-28 =48 >0, 解得 m2<7,所以 x1+x2=- ,x1x2= , 所以 x0= =- ,y0=x0+m= , 所以 N ,依题意有 AM⊥BM,MN⊥l, - 2 - 由 MN⊥l,可得 ×1=-1,可得 t=- ; 由 AM⊥BM 可得 · =-1, 因为 y1=x1+m,y2=x2+m,代入上式化简可得 2x1x2+ +(m-t)2=0, 则 -( )2+( )2=0,解得 m=± , 当 m= 时,点 M 满足题意,当 m=- 时,点 M 满足题意. 2.如图,已知椭圆 C1: + =1(b>0)的左焦点 F 与抛物线 C2:y2=-2px(p>0)的焦点重合,M 是 C1 与 C2 在第二 象限内的交点,抛物线的准线与 x 轴交于点 E,且|ME|= . (1)求椭圆 C1 及抛物线 C2 的方程. (2)过 E 作直线 l 交椭圆 C1 于 A,B 两点,则在椭圆的长轴上是否存在点 N,使得 · 为定值?若存在, 求出点 N 的坐标及定值;若不存在,请说明理由. 【解析】(1)由两曲线焦点重合,知 = , 由椭圆的对称性,知 E 为椭圆的右焦点,连接 MF, 由椭圆的定义知|MF|+|ME|=4, - 3 - 则|MF|=4- = . 设 M(xM,yM),过点 M 作准线的垂线,垂足为 H, 由抛物线的定义知|MF|=|MH|= , 因而 yM= = ,xM=- , 代入 + =1 中,得 + =1, 与 = 联立, 得 p=2,b2=3,所以椭圆的方程为 + =1, 抛物线的方程为 y2=-4x. (2)由(1)知 E(1,0),若直线 l 的斜率存在, 设直线方程为 y=k(x-1), 由 得(3+4k2)x2-8k2x+4k2-12=0. 设 A(x1,y1),B(x2,y2), 所以 x1+x2= ,x1·x2= . 假设点 N 存在,其坐标为(m,0),其中-2≤m≤2, · =(x1-m,y1)·(x2-m,y2)=(x1-m)·(x2-m)+k(x1-1)·k(x2-1) =(1+k2)x1x2-(m+k2)(x1+x2)+m2+k2 - 4 - =(1+k2) -(m+k2) +m2+k2 = . 若 · 为定值,则满足 = , 得 m= ,定值为- . 当直线 l 的斜率不存在时,直线 l 的方程为 x=1, 不妨设其与椭圆 + =1 的交点为 A 1, ,B 1,- ,又 N ,0 , 则 · = - , · - ,- =- , 综上,在椭圆的长轴上存在点 N ,0, 使得 · =- ,为定值.