高中数学（人教A版）必修3能力强化提升及单元测试2-2-1 5页

‎2.2　用样本估计总体 ‎2.2.1　用样本的频率分布估计总体分布 双基达标　(限时20分钟) ‎1．用样本频率分布估计总体频率分布的过程中，下列说法正确的是 (　　)．‎ A．总体容量越大，估计越精确 B．总体容量越小，估计越精确 C．样本容量越大，估计越精确 D．样本容量越小，估计越精确 解析　由用样本估计总体的性质可得．‎ 答案　C ‎2．频率分布直方图中，小长方形的面积等于 (　　)．‎ A．组距 B．频率 ‎ C．组数 D．频数 解析　根据小长方形的宽及高的意义，可知小长方形的面积为一组样本数据的频率．‎ 答案　B ‎3．一个容量为100的样本，其数据的分组与各组的频数如下表 组别 ‎(0,10]‎ ‎(10,20]‎ ‎(20,30]‎ ‎(30,40]‎ ‎(40,50]‎ ‎(50,60]‎ ‎(60,70]‎ 频数 ‎12‎ ‎13‎ ‎24‎ ‎15‎ ‎16‎ ‎13‎ ‎7‎ 则样本数据落在(10,40)上的频率为 (　　)．‎ A．0.13 B．0.39 C．0.52 D．0.64‎ 解析　由题意可知频数在(10,40]的有：13＋24＋15＝52，由频率＝频数÷总数可得0.52.‎ 答案　C ‎4．一个容量为n的样本，分成若干组，已知甲组的频数和频率分别为36和，则容量n＝‎ ‎________，且频率为的乙组的频数是________．‎ 解析　抽样时要保证每个个体被抽到的机会均等，＝，所以n＝36×4＝144，同理＝，x＝24.‎ 答案　144　24‎ ‎5．为了帮助班上的两名贫困生解决经济困难，班上的20名同学捐出了自己的零花钱，他们捐款数(单位：元)如下：19,20,25,30,24,23,25,29,27,27,28,28,26,27,21,30,20,19,22,20.班主任老师准备将这组数据制成频率分布直方图，以表彰他们的爱心．制图时先计算最大值与最小值的差是________．若取组距为2，则应分成________组；若第一组的起点定为18.5，则在[26.5,28.5)内的频数为________．‎ 解析　由题意知，极差为30－19＝11；由于组距为2，则＝5.5不是整数，所以取6组；捐款数落在[26.5,28.5)内的有27,27,28,28,27共5个，因此频数为5.‎ 答案　11　6　5‎ ‎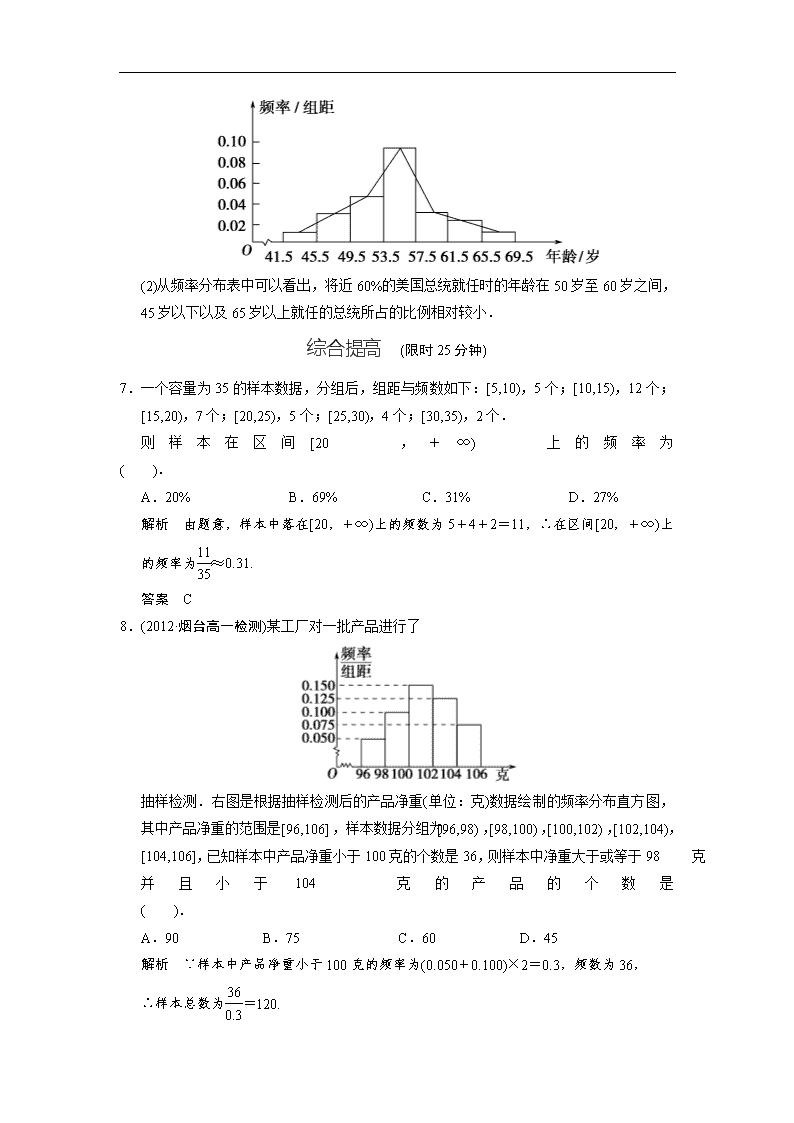6．美国历届总统中，就任时年纪最小的是罗斯福，他于1901年就任，当时年仅42岁；就任时年纪最大的是里根，他于1981年就任，当时69岁．下面按时间顺序(从1789年的华盛顿到2009年的奥巴马，共44任)给出了历届美国总统就任时的年龄：‎ ‎57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48‎ ‎(1)将数据进行适当的分组，并画出相应的频率分布直方图和频率分布折线图．‎ ‎(2)用自己的语言描述一下历届美国总统就任时年龄的分布情况．‎ 解　(1)以4为组距，列表如下：‎ 分组 频数累计 频数 频率 ‎[41.5,45.5)‎ ‎2‎ ‎0.045 5‎ ‎[45.5,49.5)‎ ‎7‎ ‎0.159 1‎ ‎[49.5,53.5)‎ ‎8‎ ‎0.181 8‎ ‎[53.5,57.5)‎ ‎16‎ ‎0.363 6‎ ‎[57.5,61.5)‎ ‎5‎ ‎0.113 6‎ ‎[61.5,65.5)‎ ‎4‎ ‎0.090 9‎ ‎[65.5,69.5]‎ ‎2‎ ‎0.045 5‎ 合计 ‎44‎ ‎1.00‎ ‎(2)从频率分布表中可以看出，将近60%的美国总统就任时的年龄在50岁至60岁之间，45岁以下以及65岁以上就任的总统所占的比例相对较小．‎ 综合提高　(限时25分钟) ‎7．一个容量为35的样本数据，分组后，组距与频数如下：[5,10)，5个；[10,15)，12个；[15,20)，7个；[20,25)，5个；[25,30)，4个；[30,35)，2个．‎ 则样本在区间[20，＋∞)上的频率为 (　　)．‎ A．20% B．69% C．31% D．27%‎ 解析　由题意，样本中落在[20，＋∞)上的频数为5＋4＋2＝11，∴在区间[20，＋∞)上的频率为≈0.31.‎ 答案　C ‎8．(2012·烟台高一检测)某工厂对一批产品进行了 抽样检测．右图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96,106]，样本数据分组为[96,98)，[98,100)，[100,102)，[102,104)，[104,106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是 (　　)．‎ A．90 B．75 C．60 D．45‎ 解析　∵样本中产品净重小于100克的频率为(0.050＋0.100)×2＝0.3，频数为36，‎ ‎∴样本总数为＝120.‎ ‎∵样本中净重大于或等于98克并且小于104克的产品的频率为(0.100＋0.150＋0.125)×2＝0.75，‎ ‎∴样本中净重大于或等于98克并且小于104克的产品的个数为120×0.75＝90.‎ 答案　A ‎9．将容量为n的样本中的数据分成6组，绘制频率分布直方图．若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1，且前三组数据的频数之和等于27，则n＝________.‎ 解析　∵n×＝27，∴n＝60.‎ 答案　60‎ ‎10．如图是甲、乙两名运动员某赛季一些场次得分的茎叶图，据图可知________．‎ 甲运动员的成绩好于乙运动员；②乙运动员的成绩好于甲运动员；③甲、乙两名运 ‎ 动员的成绩没有明显的差别；④甲运动员的最低得分为0分．‎ 解析　从这个茎叶图可以看出甲运动员的得分大致对称，平均得分是30多分，乙运动员的得分除一个52分外，也大致对称，平均得分20多分．因此，甲运动员发挥比较稳定，总体得分情况比乙好．‎ 答案　①‎ ‎11．(2013·合肥高一检测)在某电脑杂志的一篇文章中，每个句子的字数如下：‎ ‎10,28,31,17,23,27,18,15,26,24,20,19,36,27,14,25,15,22,11,24,27,17‎ 在某报纸的一篇文章中，每个句子的字数如下：‎ ‎27,39,33,24,28,19,32,41,33,27,35,12,36,41,27,13,22,23,18,46,32,22‎ ‎(1)将这两组数据用茎叶图表示；‎ ‎(2)将这两组数据进行比较分析，你会得到什么结论？‎ 解　(1)‎ ‎(2)电脑杂志上每个句子的字数集中在10～30之间；而报纸上每个句子的字数集中在20～40之间．还可以看出电脑杂志上每个句子的平均字数比报纸上每个句子的平均字数要少．说明电脑杂志作为科普读物需要通俗易懂、简明．‎ ‎12．(创新拓展)如图是一个样本的频率分布直方图，且在[15,18)内频数为8.‎ ‎(1)求样本容量；‎ ‎(2)若[12,15)一组的小长方形面积为0.06，求[12,15)‎ 一组的频数；‎ ‎(3)求样本在[18,33)内的频率．‎ 解　(1)由图可知[15,18)一组对应的纵轴数值为，且组距为3，所以[15,18)一组对应的频率为×3＝.‎ 又已知[15,18)一组的频数为8，所以样本容量n＝＝50.‎ ‎(2)[12,15)一组的小长方形面积为0.06，即[12,15)一组的频率为0.06，且样本容量为50，所以[12,15)一组的频数为50×0.06＝3.‎ ‎(3)由(1)、(2)知[12,15)一组的频数为3，[15,18)一组的频数为8，样本容量为50，所以[18,33)内频数为50－3－8＝39，所以[18,33)内的频率为＝0.78.‎