人教版高三数学总复习课时作业77 9页

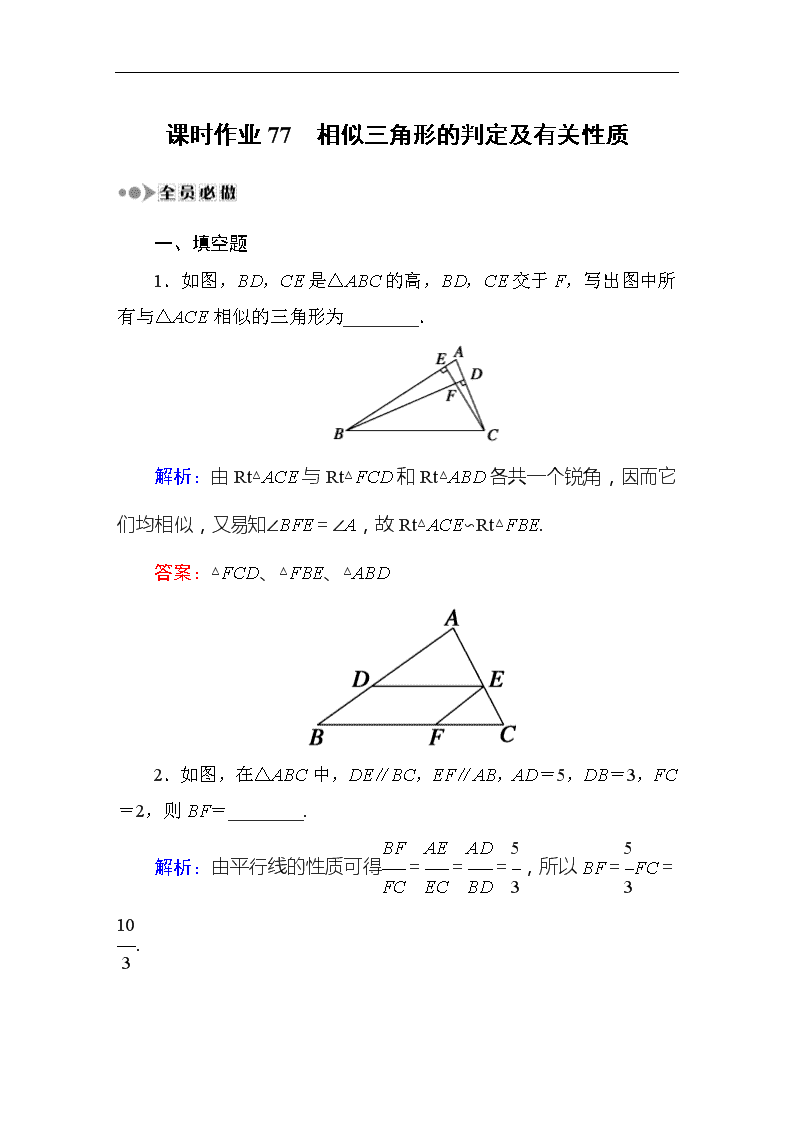
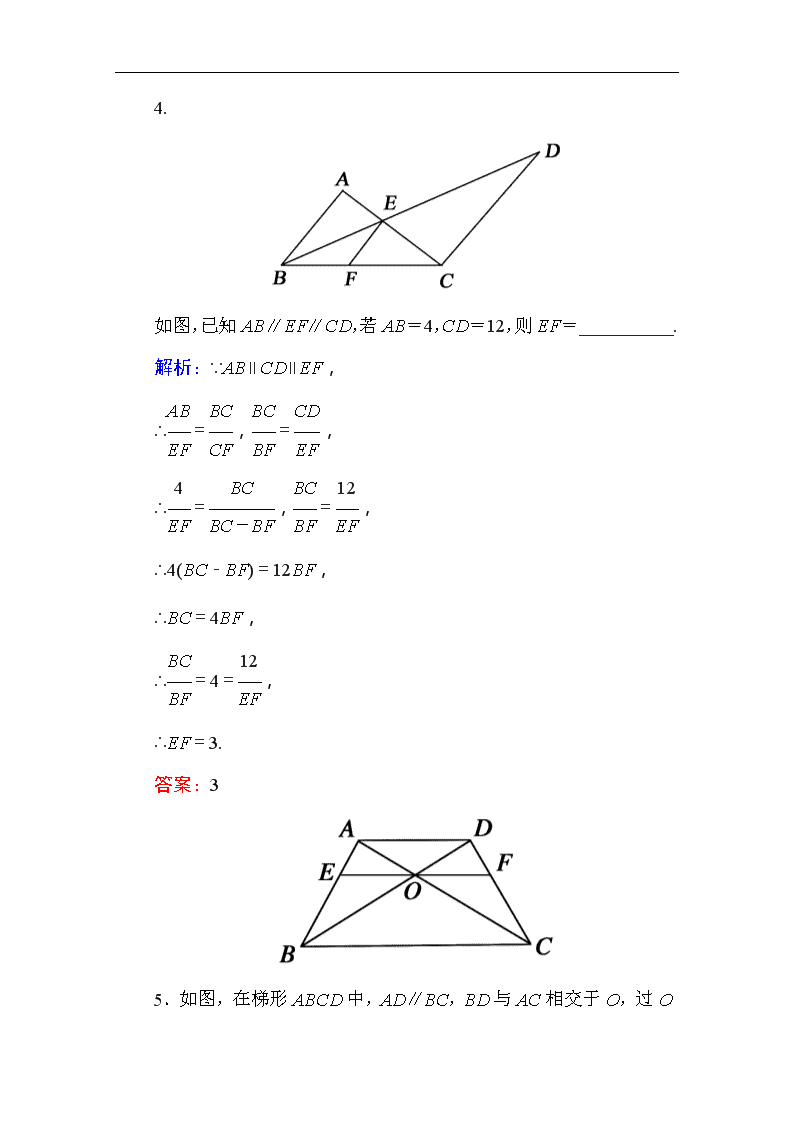
课时作业77　相似三角形的判定及有关性质 一、填空题 ‎1．如图，BD，CE是△ABC的高，BD，CE交于F，写出图中所有与△ACE相似的三角形为________．‎ 解析：由Rt△ACE与Rt△FCD和Rt△ABD各共一个锐角，因而它们均相似，又易知∠BFE＝∠A，故Rt△ACE∽Rt△FBE.‎ 答案：△FCD、△FBE、△ABD ‎2．如图，在△ABC中，DE∥BC，EF∥AB，AD＝5，DB＝3，FC＝2，则BF＝________.‎ 解析：由平行线的性质可得＝＝＝，所以BF＝FC＝.‎ 答案： ‎3．在△ABC中，∠ACB＝90°，CD⊥AB于D，ADBD＝23.则△‎ ACD与△CBD的相似比为________．‎ 解析：‎ 如图所示，在Rt△ACB中，CD⊥AB，由射影定理得：CD2＝AD·BD，‎ 又∵AD:BD＝2:3，令AD＝2x，‎ BD＝3x(x>0)，‎ ‎∴CD2＝6x2，∴CD＝x.‎ 又∵∠ADC＝∠BDC＝90°，∠A＝∠BCD.‎ ‎∴△ACD∽△CBD.‎ 易知△ACD与△CBD的相似比为＝＝.‎ 即相似比为:3.‎ 答案：:3‎ ‎4.‎ 如图，已知AB∥EF∥CD，若AB＝4，CD＝12，则EF＝__________.‎ 解析：∵AB∥CD∥EF，‎ ‎∴＝，＝，‎ ‎∴＝，＝，‎ ‎∴4(BC－BF)＝12BF，‎ ‎∴BC＝4BF，‎ ‎∴＝4＝，‎ ‎∴EF＝3.‎ 答案：3‎ ‎5．如图，在梯形ABCD中，AD∥BC，BD与AC相交于O，过O的直线分别交AB、CD于E、F，且EF∥BC，若AD＝12，BC＝20，则EF＝________.‎ 解析：∵EF∥AD∥BC，∴△OAD∽△OCB，‎ OA:OC＝AD:BC＝12:20，‎ ‎△OAE∽△CAB，OE:BC＝OA:CA＝12:32，‎ ‎∴EF＝2××20＝15.‎ 答案：15‎ ‎6．如图，在圆O中，直径AB与弦CD垂直，垂足为E，EF⊥DB，垂足为F，若AB＝6，AE＝1，则DF·DB＝________.‎ 解析：连接AD，由射影定理可知ED2＝AE·EB＝1×5＝5，又易知△EBD与△FED相似，得DF·DB＝ED2＝5.‎ 答案：5‎ ‎7．如图，等边三角形DEF内接于△ABC，且DE∥BC，已知AH⊥BC于点H，BC＝4，AH＝，则△DEF的边长为________．‎ 解析：设DE＝x，AH交DE于点M，显然MH的长度与等边三角形DEF的高相等，又DE∥BC，则＝＝，∴＝＝，解得x＝.‎ 答案： ‎8．如图，‎ 在梯形ABCD中，AB∥CD，且AB＝2CD，E、F分别是AB、BC的中点，EF与BD相交于点M.若DB＝9，则BM＝________.‎ 解析：∵E是AB的中点，‎ ‎∴AB＝2EB.‎ ‎∵AB＝2CD，∴CD＝EB.‎ 又AB∥CD，∴四边形CBED是平行四边形．‎ ‎∴CB∥DE，∴ ‎∴△EDM∽△FBM.∴＝.‎ ‎∵F是BC的中点，∴DE＝2BF.‎ ‎∴DM＝2BM.‎ ‎∴BM＝DB＝3.‎ 答案：3‎ ‎9.‎ 如图，圆O的半径为1，A，B，C是圆周上的三点，满足∠ABC＝30°，过点A做圆O的切线与OC的延长线交于点P，则PA＝________.‎ 解析：连接AO，AC，因为∠ABC＝30°，所以∠CAP＝30°，∠AOC＝60°，△AOC为等边三角形，则∠ACP＝120°，∴∠APC＝30°，∴△ACP为等腰三角形，且AC＝CP＝1，∴PA＝2×1×sin60°＝.‎ 答案： 二、解答题 ‎10．已知△ABC中，BF⊥AC于点F，CE⊥AB于点E，BF和CE相交于点P，求证：‎ ‎(1)△BPE∽△CPF；‎ ‎(2)△EFP∽△BCP.‎ 证明：(1)∵BF⊥AC于点F，CE⊥AB于点E，‎ ‎∴∠BFC＝∠CEB.‎ 又∵∠CPF＝∠BPE，∴△CPF∽△BPE.‎ ‎(2)由(1)得△CPF∽△BPE，∴＝.‎ 又∵∠EPF＝∠BPC，∴△EFP∽△BCP.‎ ‎11．如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，DF⊥AC于F，DE⊥AB于E，求证：‎ ‎(1)AB·AC＝BC·AD；‎ ‎(2)AD3＝BC·CF·BE.‎ 证明：(1)在Rt△ABC中，AD⊥BC，‎ ‎∴S△ABC＝AB·AC＝BC·AD.‎ ‎∴AB·AC＝BC·AD.‎ ‎(2)Rt△ADB中，DE⊥AB，由射影定理可得 BD2＝BE·AB，同理CD2＝CF·AC，‎ ‎∴BD2·CD2＝BE·AB·CF·AC.‎ 又在Rt△BAC中，AD⊥BC，∴AD2＝BD·DC，‎ ‎∴AD4＝BE·AB·CF·AC，‎ 又AB·AC＝BC·AD.即AD3＝BC·CF·BE.‎ ‎1．如图，在△ABC中，D为BC边的中点，E为AD上的一点，延长BE交AC于点F.若＝，求的值．‎ 解：‎ 如图，过点A作AG∥BC，‎ 交BF的延长线于点G.‎ ‎∵＝，∴＝.‎ 又∵△AGE∽△DBE，‎ ‎∴＝＝.‎ ‎∵D为BC中点，BC＝2BD，‎ ‎∴＝.‎ ‎∵△AGF∽△CBF，∴＝＝，∴＝.‎ ‎2．如图，AB为⊙O的直径，直线CD与⊙O相切于E，AD垂直CD于D，BC垂直CD于C，EF垂直AB于F，连接AE，BE.‎ 求证：(1)∠FEB＝∠CEB；‎ ‎(2)EF2＝AD·BC.‎ 证明：(1)由直线CD与⊙O相切，‎ 得∠CEB＝∠EAB.‎ 由AB为⊙O的直径，得AE⊥EB，‎ 从而∠EAB＋∠EBF＝；‎ 又EF⊥AB，得∠FEB＋∠EBF＝.‎ 从而∠FEB＝∠EAB.故∠FEB＝∠CEB.‎ ‎(2)由BC⊥CE，EF⊥AB，∠FEB＝∠CEB，BE是公共边，‎ 得Rt△BCE≌Rt△BFE，所以BC＝BF.‎ 同理可证Rt△ADE≌Rt△AFE，得AD＝AF.‎ 又在Rt△AEB中，EF⊥AB，‎ 故EF2＝AF·BF，‎ 所以EF2＝AD·BC.‎