云南省云天化中学2019-2020学年高二下学期开学考试数学（文科）试题 11页

云天化中学2019—2020学年度下学期入学考试 高二年级数学试卷（文科）‎ 第Ⅰ卷（选择题）‎ 一、选择题:（每小题分，共分．每小题只有一个选项符合题意．）‎ ‎1.在复平面内，复数对应的点到直线的距离是（ ）‎ A. B. C. D. 1‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 化简复数得出对应点，根据点到直线距离公式即可求解.‎ ‎【详解】,所以复数对应的点为(1，1)，‎ 点(1，1)到直线y＝x＋1的距离为＝.‎ 故选:B．‎ ‎【点睛】此题考查复数的基本运算，根据复数的几何意义得其在平面内对应点，根据点到平面距离公式求解.‎ ‎2.用反证法证明命题“设为实数，则方程至少有一个实根”时，要做的假设是（　　）‎ A. 方程没有实根 B. 方程至多有一个实根 C. 方程至多有两个实根 D. 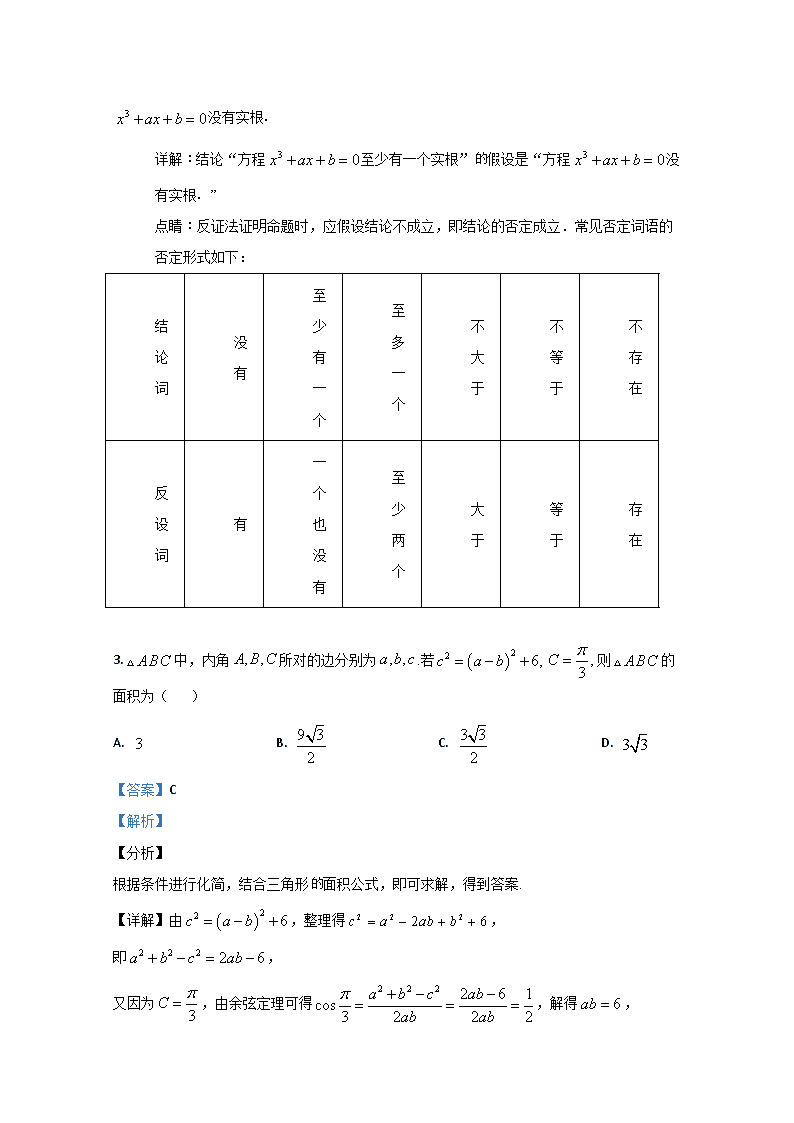方程恰好有两个实根 ‎【答案】A ‎【解析】‎ 分析：反证法证明命题时，假设结论不成立．至少有一个的对立情况为没有．故假设为方程 没有实根．‎ 详解：结论“方程至少有一个实根”假设是“方程没有实根．”‎ 点睛：反证法证明命题时，应假设结论不成立，即结论的否定成立．常见否定词语的否定形式如下：‎ 结论词 没有 至少有一个 至多一个 不大于 不等于 不存在 反设词 有 一个也没有 至少两个 大于 等于 存在 ‎3.中，内角所对的边分别为.若则的面积为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据条件进行化简，结合三角形面积公式，即可求解，得到答案.‎ ‎【详解】由，整理得，‎ 即，‎ 又因为，由余弦定理可得，解得，‎ 所以三角形的面积为.‎ 故选：C.‎ ‎【点睛】本题主要考查了解三角形的余弦定理的应用，以及三角形面积的计算，其中解答中根据余弦定理求得是解答本题的关键，着重考查了推理与运算能力.‎ ‎4.若将函数图象向右平移个单位，所得图象关于轴对称，则的最小值是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 把函数的解析式利用辅助角公式化成余弦型函数解析式形式，然后求出向右平移个单位后函数的解析式，根据题意，利用余弦型函数的性质求解即可.‎ ‎【详解】，该函数求出向右平移个单位后得到新函数的解析式为：，由题意可知：函数的图象关于轴对称，所以有 ‎ 当时，有最小值，最小值为.‎ 故选：B ‎【点睛】本题考查了余弦型函数的图象平移，考查了余弦型函数的性质，考查了数学运算能力.‎ ‎5.某学校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是17.5，30]，样本数据分组为17.5，20），20，22.5），22.5,25），25，27.5），27.5，30）.根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是（ ）‎ A. 56 B. ‎60 ‎C. 140 D. 120‎ ‎【答案】C ‎【解析】‎ ‎【详解】试题分析：由题意得，自习时间不少于小时的频率为，故自习时间不少于小时的频率为，故选C.‎ 考点：频率分布直方图及其应用．‎ ‎6.（2017新课标全国卷Ⅲ文科）已知椭圆C：的左、右顶点分别为A1，A2，且以线段A‎1A2为直径的圆与直线相切，则C的离心率为 A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ 以线段为直径的圆的圆心为坐标原点，半径为，圆的方程为，‎ 直线与圆相切，所以圆心到直线的距离等于半径，即，‎ 整理可得，即即，‎ 从而，则椭圆的离心率，‎ 故选A.‎ ‎【名师点睛】解决椭圆和双曲线的离心率的求值及取值范围问题，其关键就是确立一个关于的方程或不等式，再根据的关系消掉得到的关系式，而建立关于的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.‎ 第II卷（非选择题）‎ 二、填空题：（每小题分，共分．）‎ ‎7.观察下列等式 照此规律，第个等式为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据式子的开始项和中间一项及右边结果的特点得出.‎ ‎【详解】根据题意，由于观察下列等式 照此规律，等式左边的第一个数就是第几行的行数，且相加的连续自然数的个数是中间数字，右边是最中间数字的平方，故第个等式为.‎ ‎【点睛】本题考查了归纳推理，属于中档题．‎ ‎8.（2017新课标全国II理科）等差数列的前项和为，，，则____________．‎ ‎【答案】‎ ‎【解析】‎ 设等差数列的首项为，公差为，由题意有 ，解得 ，‎ 数列的前n项和，‎ 裂项可得，‎ 所以．‎ 点睛:等差数列的通项公式及前n项和公式，共涉及五个量a1，an，d，n，Sn，知其中三个就能求另外两个，体现了用方程的思想解决问题．数列的通项公式和前n项和公式在解题中起到变量代换作用，而a1和d是等差数列的两个基本量，用它们表示已知和未知是常用得方法．使用裂项法求和时，要注意正、负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点．‎ ‎9.已知复数（i是虚数单位），则________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 化简复数，根据模长公式求解.‎ ‎【详解】，所以．‎ 故答案为：‎ ‎【点睛】此题考查复数的基本运算，关键在于熟练掌握复数的运算法则，根据模长公式计算模长.‎ ‎10.记函数的定义域为,在区间上随机取一个数，则的概率是________．‎ ‎【答案】‎ ‎【解析】‎ 由，即，得，根据几何概型的概率计算公式得的概率是，故答案为.‎ 三、解答题：(解答应写出文字说明、证明过程或演算步骤．其中第题分，每题分，每题分共分．)‎ ‎11.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：）得频率分布直方图如下：‎ ‎（1）设两种养殖方法的箱产量相互独立，记表示事件：“旧养殖法的箱产量低于，新养殖法的箱产量不低于”，估计的概率；‎ ‎（2）填写下面列联表，并根据联表判断是否有的把握认为箱产量与养殖方法有关：‎ 箱产量 箱产量 旧养殖法 新养殖法 附：‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎（3）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01）‎ ‎【答案】（1）（2）填表见解析，有的把握认为箱产量与养殖方法有关（3）‎ ‎【解析】‎ 分析】‎ ‎（1）利用独立事件概率公式求得事件的概率估计值；‎ ‎（2）写出列联表计算，得到答案.‎ ‎（3）结合频率分布直方图估计中位数计算得到答案..‎ ‎【详解】（1）记表示事件“旧养殖法的箱产量低于”，表示事件“新养殖法的箱产量不低于”，由题意知，‎ 旧养殖法的箱产量低于的频率为，故的估计值为0.62.‎ 新养殖法的箱产量不低于的频率为，‎ 故的估计值为0.66.‎ 因此事件的概率估计值为.‎ ‎（2）根据箱产量的频率分布直方图得列联表 箱产量 箱产量 旧养殖法 ‎62‎ ‎38‎ 新养殖法 ‎34‎ ‎66‎ ‎.‎ 由于，故有的把握认为箱产量与养殖方法有关.‎ ‎（3）因为新养殖法的箱产量频率分布直方图中，箱产量低于的直方图面积为 ‎，‎ 箱产量低于的直方图面积为，‎ 故新养殖法箱产量的中位数的估计值为.‎ ‎【点睛】本题考查了概率的计算，独立性检验，中位数，意在考查学生的计算能力和应用能力.‎ ‎12.如图，A，B是海面上位于东西方向相距海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距海里的C点的救援船立即即前往营救，其航行速度为30海里/小时，该救援船到达D点需要多长时间？‎ ‎【答案】救援船到达D点需要1小时．‎ ‎【解析】‎ ‎【详解】‎ 海里 又海里 中，由余弦定理得,‎ 海里，则需要的时间 答：救援船到达D点需要1小时 ‎13.如图，在四棱锥P﹣ABCD中，PA⊥面ABCD，AB=BC=2，AD=CD=，PA=，∠ABC=120°，G为线段PC上的点．‎ ‎（Ⅰ）证明：BD⊥平面PAC；‎ ‎（Ⅱ）若G是PC的中点，求DG与PAC所成的角的正切值；‎ ‎（Ⅲ）若G满足PC⊥面BGD，求的值．‎ ‎【答案】（1）见解析 （2）（3）‎ ‎【解析】‎ 试题分析：（Ⅰ）利用直线和平面垂直的判定定理证得BD⊥面PAC．‎ ‎（Ⅱ）由三角形的中位线性质以及条件证明∠DGO为DG与平面PAC所成的角，求出GO和AC的值，可得OC、OD的值，再利用直角三角形中的边角关系求得tan∠DGO的值．‎ ‎（Ⅲ）由△COG∽△CAP，可得，解得GC值，可得PG=PC﹣GC 的值，从而求得的值．‎ 考点：直线与平面垂直的判定；直线与平面所成的角．‎ 点评：本题考查了直线和平面垂直的判定定理的应用，求直线和平面所成的角的求法．‎ ‎ ‎