华附、省实、深中、广雅2020届高三数学（文）四校联考试卷（Word版附答案） 12页

www.ks5u.com 数 学（文科）‎ 本试卷分选择题和非选择题两部分，共5页，满分150分，考试用时120分钟.‎ 注意事项：‎ 1. 答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卡上.‎ 2. 答案一律做在答题卡上，选择题的每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案.‎ 3. 非选择题必须用黑色字迹的钢笔或签字笔用答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液.不按以上要求作答的答案无效.‎ 4. 保持答题卡的整洁，不要折叠，不要弄破.‎ 第一部分 选择题（共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分. 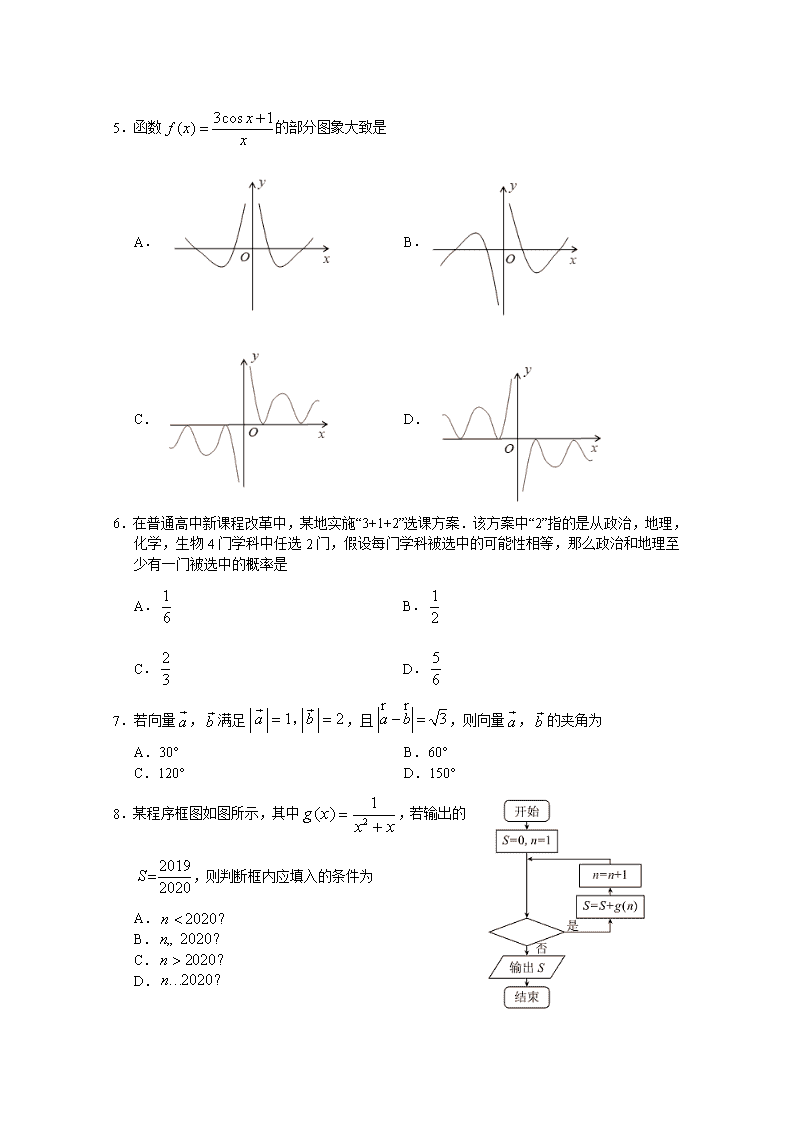在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知集合，则 A． B． C． D．‎ ‎2．已知，，则z对应的点Z的轨迹为 A．椭圆 B．双曲线 C．抛物线 D．线段 ‎3．设，，那么 A． B．‎ C． D．‎ ‎4．“干支纪年法”是中国历法上自古以来使用的纪年方法，甲，乙，丙，丁，戊，己，庚，辛，壬，癸被称为“十天干”，子，丑，寅，卯，辰，巳，午，未，申，酉，戌，亥叫做“十二地支”．“天干”以“甲”字开始，“地支”以“子”字开始，两者按干支顺序相配，组成了干支纪年法，其相配顺序为：甲子，乙丑，丙寅，…癸酉，甲戌，乙亥，丙子，…癸未，甲申，乙酉，丙戌，…癸巳，…，共得到60个组合，称六十甲子，周而复始，无穷无尽．2019年是“干支纪年法”中的己亥年，那么2026年是“干支纪年法”中的 A．甲辰年 B．乙巳年 C．丙午年 D．丁未年 ‎5．函数的部分图象大致是 A． B．‎ C． D．‎ ‎6．在普通高中新课程改革中，某地实施“3+1+2”选课方案．该方案中“2”指的是从政治，地理，化学，生物4门学科中任选2门，假设每门学科被选中的可能性相等，那么政治和地理至少有一门被选中的概率是 A． B． C． D．‎ ‎7．若向量，满足，且，则向量，的夹角为 A．30° B．60° ‎ C．120° D．150°‎ ‎8．某程序框图如图所示，其中，若输出的，则判断框内应填入的条件为 A． ‎ B． ‎ C． ‎ D．‎ ‎9．设等差数列的前项和为，若，则等于 A．18 B．36 C．45 D．60‎ ‎10．已知函数，那么下列命题中假命题是 A．是偶函数 B．在上恰有一个零点 C．是周期函数 D．在上是增函数 ‎11．在三棱锥中，，，则三棱锥外接球的体积是 A． B． C． D．‎ ‎12．已知椭圆的焦点为，，过的直线与交于A，B两点．若，，则椭圆的方程为 A． B． C． D．‎ 第二部分 非选择题（共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分. 请将答案填在答题卡的相应位置上.‎ ‎13．曲线在点处的切线方程为 .‎ ‎14．某工厂为了解产品的生产情况，随机抽取了100个样本．若样本数据，，…，的方差为16，则数据，，…，的方差为 .‎ ‎15．设F为双曲线C：（a>0，b>0）的右焦点，O为坐标原点，以为直径的圆与圆交于两点．若，则C的离心率为 .‎ ‎16. 在中，角，，的对边分别为，且角为锐角，则面积的最大值为 .‎ 三、 解答题：满分70分. 解答应写出文字说明、证明过程或演算步骤. 第17～21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.‎ ‎（一）必考题：共60分.‎ ‎17．(本小题满分12分) ‎ 在等比数列中，公比为，．‎ ‎（Ⅰ）求数列{}的通项公式；‎ ‎（Ⅱ）设，求数列的前项和．‎ ‎18．(本小题满分12分) ‎ 如图，在直三棱柱中，，‎ 是的中点，.‎ ‎（Ⅰ）求证：∥平面；‎ ‎（Ⅱ）异面直线和所成角的余弦值为 ‎，求几何体的体积.‎ ‎19．(本小题满分12分) ‎ ‎ 已知某保险公司的某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：‎ 上年度出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 保费（元）‎ 随机调查了该险种的400名续保人在一年内的出险情况，得到下表：‎ 出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 频数 ‎280‎ ‎80‎ ‎24‎ ‎12‎ ‎4‎ 该保险公司这种保险的赔付规定如下：‎ 出险序次 第1次 第2次 第3次 第4次 第5次 及以上 赔付金额（元）‎ ‎0‎ 将所抽样本的频率视为概率.‎ ‎（Ⅰ）求本年度续保人保费的平均值的估计值；‎ ‎（Ⅱ）按保险合同规定，若续保人在本年度内出险3次，则可获得赔付 元；若续保人在本年度内出险6次，则可获得赔付元；依此类推，求本年度续保人所获赔付金额的平均值的估计值；‎ ‎（Ⅲ）续保人原定约了保险公司的销售人员在上午～之间上门签合同，因为续保人临时有事，外出的时间在上午～之间，请问续保人在离开前见到销售人员的概率是多少？‎ ‎20．(本小题满分12分) ‎ ‎ 已知点，在椭圆上，其中为椭圆的离心率，椭圆的右顶点为.‎ ‎（Ⅰ）求椭圆的方程；‎ ‎ （Ⅱ）直线过椭圆的左焦点交椭圆于，两点， 直线,分别与直线交于，两点，求证： .‎ ‎21．(本小题满分12分) ‎ ‎ 已知函数有两个极值点，其中.‎ ‎（Ⅰ）求实数的取值范围；‎ ‎（Ⅱ）当时，求的最小值.‎ ‎（二）选考题：共10分. 请考生从给出的第22、23题中任选一题作答，并用2B铅笔在答题卡上把所选题目对应的题号涂黑，注意所做题目的题号必须与所涂题号一致，如果多做，则按所做的第一题计分.‎ ‎22．(本小题满分10分) 选修4-4；坐标系与参数方程 在直角坐标系中，以坐标原点为极点，轴正半轴为极轴，建立极坐标系，‎ 曲线，曲线.‎ ‎（Ⅰ）求曲线的直角坐标方程；‎ ‎（Ⅱ）已知曲线与轴交于两点，为曲线上任一点，‎ 求的最小值.‎ ‎23．(本小题满分10分) 选修4-5：不等式选讲 已知函数的单调递增区间为.‎ ‎（Ⅰ）求不等式的解集；‎ ‎（Ⅱ）设，证明：.‎ 数学（文科）参考答案 一、选择题 CDCCB DBACD BA 二、填空题 ‎ 13． 14．64 15． 16．‎ 三、解答题 ‎17．解：（Ⅰ）因为公比为的等比数列中，‎ ‎ ‎ 所以，当且仅当时成立.----------------------2分 此时公比,　　---------------------------------3分 所以 ------------------------------------------------5分 ‎ （Ⅱ）因为 ‎ 所以 ‎ ‎ --------------7分 ‎--------8分 ‎ --------9分 ‎ -------------------------11分 ‎ ‎ ‎ 故数列的前项和----------------------------12分 ‎18. 解：（Ⅰ）如图，连结交于点，连结---------------------------1分 ‎ 因为在直三棱柱中，四边形是矩形 ‎ 所以 点是的中点---------------------------------------------2分 ‎ 因为是的中点 ‎ 所以 ∥---------------------------------------------------3分 ‎ 因为平面，平面 ‎ 所以 ∥平面---------------------------------------------4分 ‎ （Ⅱ）因为棱柱是直三棱柱 ‎ 所以 ‎ ‎ 因为 ‎ 所以 ---------------------------------------------------5分 ‎ 因为异面直线和所成角的余弦值为 ‎ 所以 --------------------------------------------6分 ‎ 因为 所以 ----------------------------------------------------7分 根据余弦定理，在中，‎ 可得----------------------------------------------8分 因为，所以 由勾股定理可得 ‎ 因为 所以 同理------------------------------------------------9分 所以 --------------------------------10分 ‎ ‎ ‎ ‎ 所以 几何体的体积为.----------------------------------12分 ‎19. 解：（Ⅰ）由题意可得 保费（元）‎ 概率 ‎0.7‎ ‎0.2‎ ‎0.06‎ ‎0.03‎ ‎0.01‎ 本年度续保人保费的平均值的估计值为 ‎；----4分 ‎（Ⅱ）由题意可得 赔偿金额（元）‎ ‎0‎ 概率 ‎0.7‎ ‎0.2‎ ‎0.06‎ ‎0.03‎ ‎0.01‎ 本年度续保人所获赔付金额的平均值的估计值 ‎；-----8分 ‎（Ⅲ）设保险公司销售人员到达的时间为，续保人离开的时间为，看成平面上的点，全部结果所构成的区域为，‎ 则区域的面积---------------------------------9分 事件表示续保人在离开前见到销售人员，‎ 所构成的区域为---10分 ‎ 即图中的阴影部分，其面积------------------11分 所以，即续保人在离开前见到销售人员的概率是--------12分 ‎（备注：第Ⅰ、Ⅱ参考答案中的表格填写正确各得2分；示意图不要求作出）‎ ‎ ‎ ‎20. 解：（Ⅰ）依题意得 ‎ ‎ 解得 ‎ 所以 椭圆的方程为-----------------------------------3分 ‎ （Ⅱ）由（Ⅰ）得， -----------------------------------------------4分 如图，设，，，，‎ 把直线代入椭圆方程，得 ‎ 所以--------------------------5分 因为三点共线，得------------------------6分 所以 ①-------------7分 同理，由三点共线，得 ②-------------8分 因为 ③-------------9分 所以把①②代入③得 ‎ --10分 ‎ ----11分 ‎ ‎ 所以 --------------------------------------------------12分 ‎21. 解：（Ⅰ）依题意得的定义域为，----------1分 ‎ 因为函数有两个极值点 ‎ 所以方程有两个不相等的正根 ‎ 所以--------------------------------------------3分 解得 ‎ 此时在和上单调递增，在上单调递减 所以 实数的取值范围是-------------------------------4分 ‎ （Ⅱ）因为，是方程的两个根，‎ 所以，‎ 因为，‎ 所以 ，---------------------------------6分 所以 ‎--------------------------------8分 令，，则 即在上单调递减------------------------------------------10分 因为 ， 所以 ‎ 所以 ，即 ‎ 所以 ， 即 ‎ 所以 ，‎ 所以 ------------------------------------------------------11分 因为 在上单调递减 所以的最小值为 即的最小值为.--------------------------------12分 ‎22. 解：（Ⅰ）因为，‎ 所以曲线的直角坐标方程为-----------------2分 ‎ 因为----------------4分 ‎ 所以曲线的直角坐标方程为------------------------5分 ‎ （Ⅱ）因为曲线与轴交于两点------------6分 点关于直线的对称点为-------------8分 ‎ 所以 ‎ ‎ 所以的最小值为----------------------------------10分 ‎23. 解：（Ⅰ）依题意得--------------------------------------------------1分 ‎ 所以不等式化为 ‎ 当时，原不等式化为，，得------2分 ‎ 当时，原不等式化为，，‎ 得-----------------------------------------3分 ‎ 当时，原不等式化为，，得------------4分 ‎ 所以，不等式的解集----------5分 ‎ （Ⅱ）要证明，只需证明 ‎ 即要证明--------------------------------------6分 ‎ 因为，所以---------------8分 因为--------9分 ‎ 所以 ‎ ‎ 即得证 ---------------------------------------------10分