【数学】2020届一轮复习人教版进位制教案 3页

‎ ‎ 授课题目 进位制 拟 1 课时 第 1课时 明确目标 了解各种进位制与十进制之间转换的规律，会利用各种进位制与十进制之间的联系进行各种进位制之间的转换。‎ 重点难点 重点：各进位制表示数的方法及各进位制之间的转换 难点：除k去余法的理解以及各进位制之间转换的程序框图的设计 课型 ‎□讲授 □习题 □复习 □讨论 □其它 教 学 内 容 与 教 师 活 动 设 计 学生活动过程 一、先学后讲 ‎（一）创设情景，揭示课题 我们常见的数字都是十进制的,但是并不是生活中的每一种数字都是十进制的.比如时间和角度的单位用六十进位制,电子计算机用的是二进制.那么什么是进位制?不同的进位制之间又又什么联系呢?‎ ‎（二）研探新知 进位制是一种记数方式，用有限的数字在不同的位置表示不同的数值。可使用数字符号的个数称为基数，基数为n，即可称n进位制，简称n进制。现在最常用的是十进制，通常使用10个阿拉伯数字0-9进行记数。‎ 对于任何一个数，我们可以用不同的进位制来表示。比如：十进数57，可以用二进制表示为111001，也可以用八进制表示为71、用十六进制表示为39，它们所代表的数值都是一样的。‎ 表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表示5进制数.‎ 电子计算机一般都使用二进制,下面我们来进行二进制与十进制之间的转化 例1 把二进制数110011(2)化为十进制数.‎ 解:110011=1*25+1*24+0*23+1*24+0*22+1*21+1*20‎ ‎ =32+16+2+1‎ 教师提出问题 ‎ =51‎ 例2 把89化为二进制数.‎ 解:根据二进制数满二进一的原则,用2连续去除89或所得商,然后去余数.‎ 具体的计算方法如下:‎ ‎89=2*44+1 44=2*22+0 22=2*11+0 11=2*5+1 5=2*2+1‎ 所以:89=2*(2*(2*(2*(2*2+1)+1)+0)+0)+1‎ ‎ =1*26+0*25+1*24+1*23+0*22+0*21+1*20‎ ‎ =1011001(2)‎ 这种算法叫做除2取余法,还可以用下面的除法算式表示:‎ ‎89‎ ‎44‎ ‎22‎ ‎11‎ ‎5‎ ‎2‎ ‎1‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ ‎2‎ ‎0‎ 余数 ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ 把上式中的各步所得的余数从下到上排列即可得到89=1011001(2)‎ 上述方法也可以推广为把十进制化为k进制数的算法,这种算法成为除k取余法.‎ 当数字较小时,也可直接利用各进位制表示数的特点,都是以幂的形式来表示各位数字,比如2*103表示千位数字是2,所以可以直接求出各位数字.即把89转换为二进制数时,直接观察得出89与64最接近故89=64*1+25‎ 同理:25=16*1+9‎ ‎9=8*!+1‎ 即89=64*1+16*1+8*!+1=1*26+1*24+1*23+1*20‎ 位数 ‎6‎ ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎0‎ 教师分析后，学生独立或合作完成后，教师点评 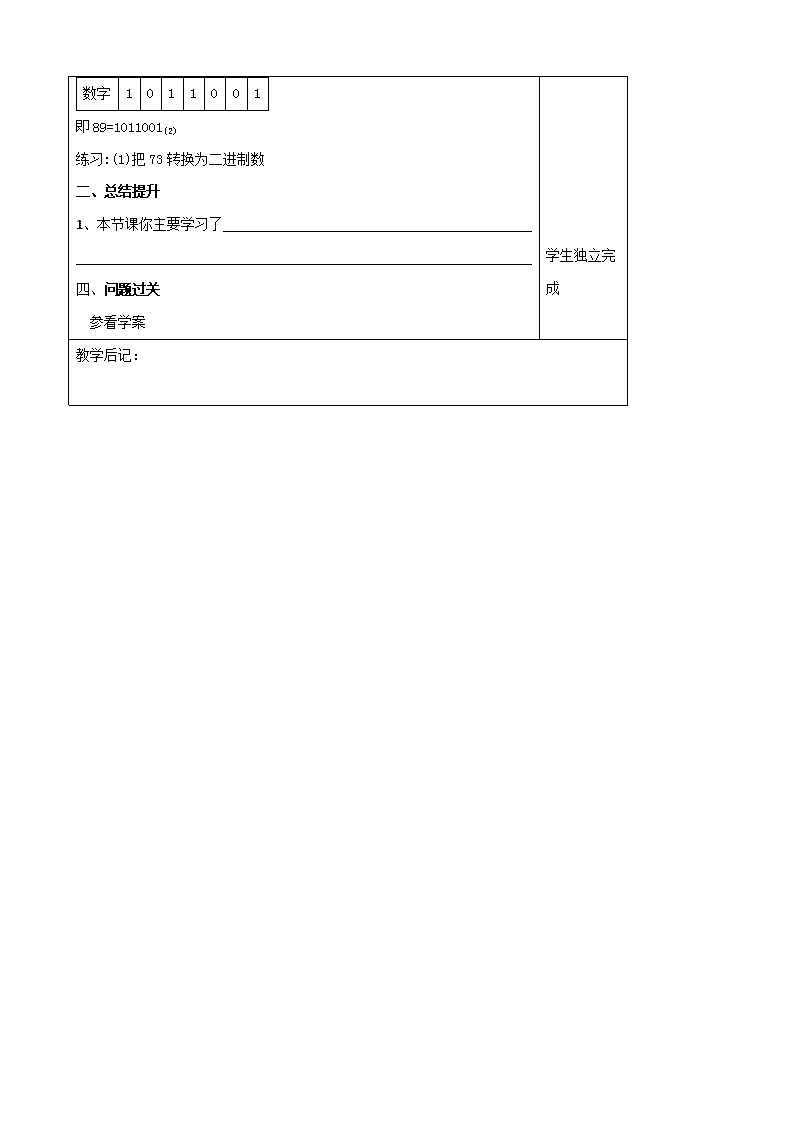数字 ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ 即89=1011001(2)‎ 练习:(1)把73转换为二进制数 二、总结提升 ‎1、本节课你主要学习了 ‎ ‎ ‎ 四、问题过关 参看学案 学生独立完成 教学后记：‎