2020-2021贵阳市七中高中必修三数学上期末模拟试卷附答案 21页

2020-2021 贵阳市七中高中必修三数学上期末模拟试卷附答案 一、选择题 1．一块各面均涂有油漆的正方体被锯成 27 个大小相同的小正方体，若将这些小正方体均 匀地搅混在一起，从中任意取出一个，则取出的小正方体两面涂有油漆的概率是 ( ) A． B． C． D． 2．已知一组数据的茎叶图如图所示，则该组数据的平均数为（ ） A．85 B．84 C．83 D．81 3．执行如图所示的程序框图，若输入 8x ，则输出的 y 值为（ ） A．3 B． 5 2 C． 1 2 D． 3 4 4．执行如图的程序框图，如果输入 72m ，输出的 6n ，则输入的 n 是（ ） A．30 B．20 C．12 D．8 5．己知某产品的销售额 y 与广告费用 x 之间的关系如下表： 若求得其线性回归方程为 6.5? 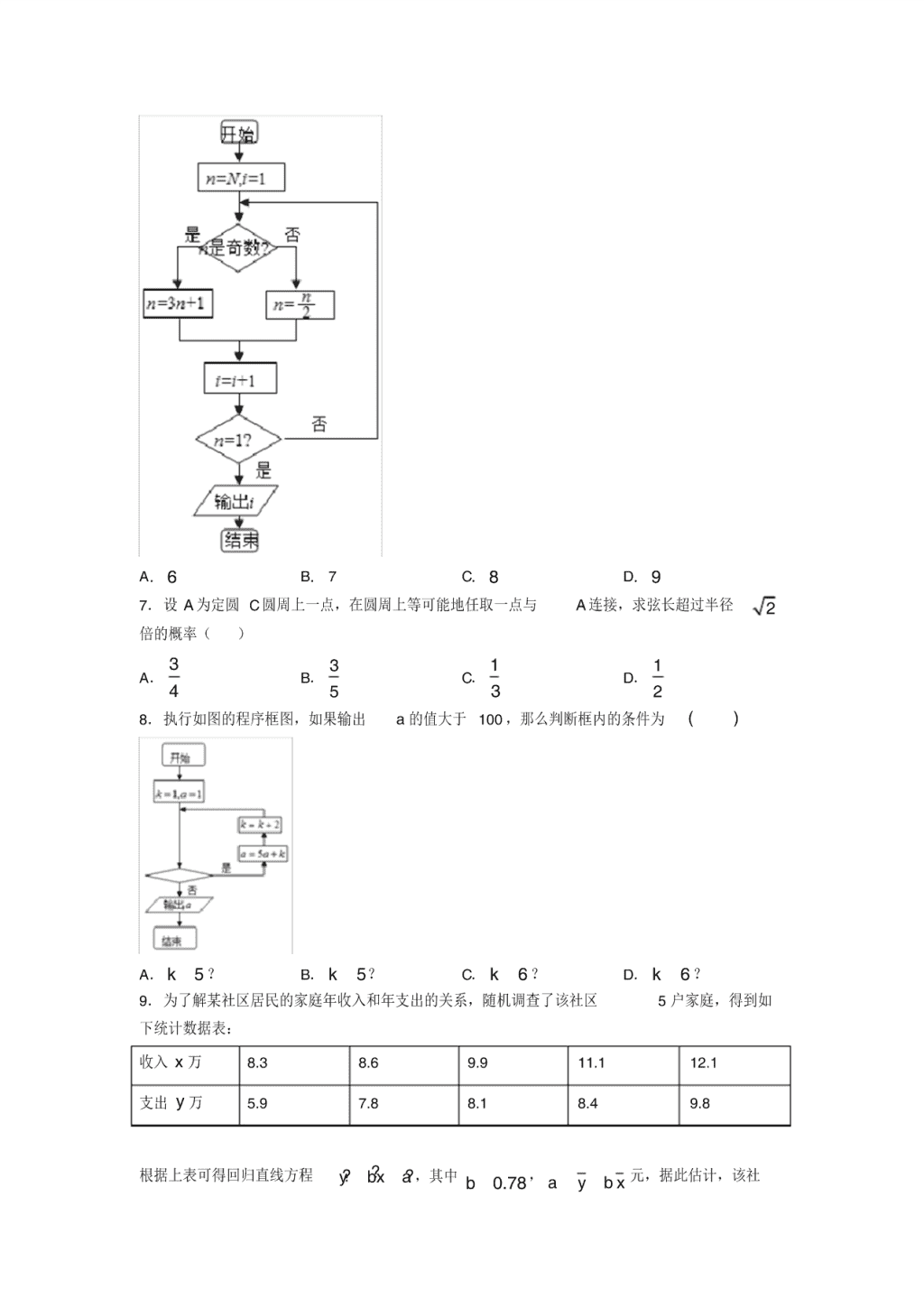?y x a ，其中 ??a y bx ，则预计当广告费用为 6 万元时 的销售额是（ ） A．42 万元 B．45 万元 C．48 万元 D．51 万元 6．日本数学家角谷静夫发现的“ 3 1x 猜想”是指：任取一个自然数，如果它是偶数， 我们就把它除以 2，如果它是奇数我们就把它乘 3再加上 1，在这样一个变换下，我们就得 到了一个新的自然数．如果反复使用这个变换，我们就会得到一串自然数，猜想就是：反 复进行上述运算后，最后结果为 1，现根据此猜想设计一个程序框图如图所示，执行该程 序框图输入的 6N ，则输出 i 值为（ ） A． 6 B． 7 C． 8 D． 9 7．设 A 为定圆 C圆周上一点，在圆周上等可能地任取一点与 A 连接，求弦长超过半径 2 倍的概率（ ） A． 3 4 B． 3 5 C． 1 3 D． 1 2 8．执行如图的程序框图，如果输出 a 的值大于 100 ，那么判断框内的条件为 ( ) A． 5k ？ B． 5k ？ C． 6k ？ D． 6k ？ 9．为了解某社区居民的家庭年收入和年支出的关系，随机调查了该社区 5 户家庭，得到如 下统计数据表： 收入 x 万 8.3 8.6 9.9 11.1 12.1 支出 y 万 5.9 7.8 8.1 8.4 9.8 根据上表可得回归直线方程 ?? ?y bx a ，其中 0.78b ， a y b x 元，据此估计，该社 区一户收入为 16 万元家庭年支出为（ ） A．12.68 万元 B．13.88 万元 C．12.78 万元 D．14.28 万元 10． 执行如图所示的程序框图，若输入 2x ，则输出的 y （ ） A． 8 B． 4 C． 4 D． 8 11． 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果 .哥德巴赫猜想是 “每个大于 2 的偶数可以表示为两个素数的和”，如 40 3 37.（注：如果一个大于 1 的 整数除 1 和自身外无其他正因数，则称这个整数为素数 .）在不超过 11 的素数中，随机选 取 2 个不同的数，其和小于等于 10 的概率是（ ） A． 1 2 B． 1 3 C． 1 4 D． 1 5 12． 小赵和小王约定在早上 7:00 至 7:15 之间到某公交站搭乘公交车去上学，已知在这段时 间内，共有 2 班公交车到达该站，到站的时间分别为 7:05，7:15，如果他们约定见车就搭 乘，则小赵和小王恰好能搭乘同一班公交车去上学的概率为（ ） A． 1 3 B． 4 9 C． 5 9 D． 2 3 二、填空题 13． 若正方形 ABCD 的边长为 4, E 为四边形上任意一点 , 则 AE 的长度大于 5 的概率等 于 ______ 14． 已知 2 件次品和 3件正品放在一起，现需要通过检测将其区分，每次随机检测一件产 品，检测后不放回，直到检测出 2件次品或者检测出 3 件正品时检测结束，则恰好检测四 次停止的概率为 _____（用数字作答）． 15． 如图，在半径为 1 的圆上随机地取两点 ,B E ，连成一条弦 BE ，则弦长超过圆内接正 BCD 边长的概率是 __________． 16．如图所示，在边长为 1 的正方形 OABC中任取一点 M ．则点 M 恰好取自阴影部分的概 率是 ． 17． 投掷一枚均匀的骰子，则落地时，向上的点数是 2 的倍数的概率是 _________， 18． 4 位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参 加公益活动的概率是 ________ 19． 在区间 [0,1] 中随机地取出两个数，则两数之和大于 4 5 的概率是 ______. 20． 某学校高一年级男生人数占该年级学生人数的 45%，在一次考试中，男、女生平均分 数依次为 72 、 74 ，则这次考试该年级学生的平均分数为 __________． 三、解答题 21． 某电子科技公司由于产品采用最新技术，销售额不断增长，最近 5 个季度的销售额数 据统计如下表（其中 2018 1Q 表示 2018年第一季度，以此类推）： 季度 2018 1Q 2018 2Q 2018 3Q 2018 4Q 2019 1Q 季度编号 x 1 2 3 4 5 销售额 y（百万元） 46 56 67 86 96 （1）公司市场部从中任选 2 个季度的数据进行对比分析，求这 2 个季度的销售额都超过 6 千万元的概率； （2）求 y 关于 x 的线性回归方程，并预测该公司 2019 3Q 的销售额 . 附：线性回归方程： y bx a$ $ $ 其中 1 1 2 22 1 1 n n i i i i i i n n i i i i x x y y x y nx y b x x x nx $ ， $ $a y bx$ 参考数据： 5 1 1183i i i x y . 22． 某校 100 名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间 是： [50,60), [60,70),[70,80),[80,90),[90,100] . （1）求图中 a 的值； （2）根据频率分布直方图，估计这 100 名学生语文成绩的平均数与中位数 . 23． 某函数的解析式由如图所示的程序框图给出 . （1）写出该函数的解析式； （2）执行该程序框图，若输出的结果为 4，求输入的实数 x 的值 . 24．从某校随机抽取 100 名学生，获得了他们一周课外阅读时间（单位：小时）的数据， 整理得到数据分组及频数分布表和频率分布直方图： （1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于 12 小时的概率； （2）求频率分布直方图中的 a， b 的值； （3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的 100 名学生该 周课外阅读时间的平均数在第几组（只需写出结论） 25． 某校高二年级 800 名学生参加了地理学科考试，现从中随机选取了 40 名学生的成绩作 为样本，已知这 40 名学生的成绩全部在 40 分至 100 分之间，现将成绩按如下方式分成 6 组：第一组 40 50， ；第二组 50 60， ；⋯⋯ ；第六组 90100， ，并据此绘制了如图所示的 频率分布直方图． （1）求每个学生的成绩被抽中的概率； （2）估计这次考试地理成绩的平均分和中位数； （3）估计这次地理考试全年级 80 分以上的人数 . 26． 一个盒子中有 5 只同型号的灯泡，其中有 3 只一等品， 2 只二等品，现在从中依次取 出 2 只，设每只灯泡被取到的可能性都相同，请用“列举法”解答下列问题： （Ⅰ）求第一次取到二等品，且第二次取到的是一等品的概率； （Ⅱ）求至少有一次取到二等品的概率 . 【参考答案】 *** 试卷处理标记，请不要删除 一、选择题 1．C 解析： C 【解析】 【分析】 先求出基本事件总数 n＝ 27，在得到的 27 个小正方体中，若其两面涂有油漆，则这个小正 方体必在原正方体的某一条棱上，且原正方体的一条棱上只有一个两面涂有油漆的小正方 体，则两面涂有油漆的小正方体共有 12 个，由此能求出在 27 个小正方体中，任取一个其 两面涂有油漆的概率． 【详解】 ∵一块各面均涂有油漆的正方体被锯成 27 个大小相同的小正方体， ∴基本事件总数 n＝27， 在得到的 27 个小正方体中， 若其两面涂有油漆，则这个小正方体必在原正方体的某一条棱上， 且原正方体的一条棱上只有一个两面涂有油漆的小正方体， 则两面涂有油漆的小正方体共有 12 个，则在 27 个小正方体中，任取一个其两面涂有油漆 的概率 P = 故选： C 【点睛】 本题考查概率的求法，考查古典概型、正方体性质等基础知识，考查推理论证能力、空间 想象能力，考查函数与方程思想，是基础题． 2．A 解析： A 【解析】 【分析】 利用茎叶图、平均数的性质直接求解． 【详解】 由一组数据的茎叶图得： 该组数据的平均数为： 1(75 81 85 89 95) 85 5 ． 故选： A． 【点睛】 本题考查平均数的求法，考查茎叶图、平均数的性质等基础知识，考查运算求解能力，是 基础题． 3．C 解析： C 【解析】 【分析】 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知该程序的作用是利用 循环计算 y 值并输出，模拟程序的运行过程，直到达到输出条件即可 . 【详解】 输入 8，第一次执行循环： 3y ，此时 5y x ， 不满足退出循环的条件，则 3x ， 第二次执行循环： 1 2 y ，此时 5 2 y x ， 满足退出循环的条件， 故输出的 y 值为 1 2 ，故选 C. 【点睛】 本题主要考查程序框图的循环结构流程图，属于中档题 . 解决程序框图问题时一定注意以下 几点： (1) 不要混淆处理框和输入框； (2) 注意区分程序框图是条件分支结构还是循环结 构； (3) 注意区分当型循环结构和直到型循环结构； (4) 处理循环结构的问题时一定要正确 控制循环次数； (5) 要注意各个框的顺序 , （6）在给出程序框图求解输出结果的试题中只 要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可 . 4．A 解析： A 【解析】 从流程图看，该程序是利用辗转相除法计算 ,m n 的最大公约数 .题设中已知 72m ，输入 的数为 n ，程序给出了它们的最大公约数为 6，比较四个数，只有 72,30 的最大公约数为 6，故输入的数 n 的值为 30，选 A. 5．C 解析： C 【解析】 【分析】 由已知求得样本点的中心的坐标，代入线性回归方程求得 ?a ，则线性回归方程可求，取 6x 求得 y 值即可． 【详解】 1 0 1 2 3 4 2 5 x ， 1 10 15 20 30 35 22 5 y ， 样本点的中心的坐标为 2,22 ， 代入 ? ? a y b x ，得 22 6.5 2 9a ． y 关于 x 得线性回归方程为 6.5 9y x ． 取 6x ，可得 6.5 6 9 48(y 万元 ) ． 故选： C． 【点睛】 本题考查线性回归方程的求法，考查计算能力，是基础题． 6．D 解析： D 【解析】 分析：由已知中的程序语句可知：该程序的功能是利用循环结构计算 n 的值并输出相应的 i 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得结论 . 详解：模拟程序的运行， 可得 6, 1n i ，不满足条件 n 是奇数， 3, 2n i ， 不满足条件 1n ，执行循环体，不满足 n 是奇数， 10, 3n i ； 不满足条件 1n ，执行循环体，不满足 n 是奇数，可得 5, 4n i ， 不满足条件 1n ，执行循环体，满足条件 n 是奇数， 16, 5n i ， 不满足条件 1n ，执行循环体，不满足 n 是奇数， 8, 6n i ； 不满足条件 1n ，执行循环体，不满足 n 是奇数， 4, 7n i ； 不满足条件 1n ，执行循环体，不满足 n 是奇数， 2, 8n i ； 不满足条件 1n ，执行循环体，不满足 n 是奇数， 1, 9n i ， 满足条件 1n ，退出循环，输出 i 的值为 9，故选 D. 点睛：本题主要考查程序框图的循环结构流程图，属于中档题 . 解决程序框图问题时一定注 意以下几点： (1) 不要混淆处理框和输入框； (2) 注意区分程序框图是条件分支结构还是循 环结构； (3) 注意区分当型循环结构和直到型循环结构； (4) 处理循环结构的问题时一定要 正确控制循环次数； (5) 要注意各个框的顺序 ,（6）在给出程序框图求解输出结果的试题中 只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可 . 7．D 解析： D 【解析】 【分析】 先找出满足条件弦的长度超过 2R 的图象的测度，再代入几何概型计算公式求解，即可得 到答案． 【详解】 根据题意可得，满足条件：“弦的长度超过 2R对应的弧”， 其构成的区域为半圆 ?NP , 则弦长超过半径 2 倍的概率 ? 1 2 NPP 圆的周长 ， 【点睛】 本题主要考查了几何概型的概率计算中的“几何度量”，对于几何概型的“几何度量”可 以线段的长度比、图形的面积比、几何体的体积比等，且这个“几何度量”只与“大小” 有关，与形状和位置无关，着重考查了分析问题和解答问题的能力． 8．C 解析： C 【解析】 【分析】 由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量 a 的值，模拟程 序的运行过程，分析循环中各变量值的变化情况，可得答案． 【详解】 由题意，模拟程序的运算，可得 k 1 ， a 1 满足判断框内的条件，执行循环体， a 6 ， k 3 满足判断框内的条件，执行循环体， a 33， k 5 满足判断框内的条件，执行循环体， a 170， k 7 此时，不满足判断框内的条件，退出循环，输出 a 的值为 170． 则分析各个选项可得程序中判断框内的“条件”应为 k 6 ？ 故选： C． 【点睛】 本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结 论，是基础题． 9．A 解析： A 【解析】 【分析】 由已知求得 x ， y ，进一步求得 $a ，得到线性回归方程，取 16x 求得 y 值即可． 【详解】 8.3 8.6 9.9 11.1 5 12.1 10x ， 5.9 7.8 8.1 8.4 9. 8 5 8y ． 又 0.78b$ ，∴ $ 8 0.78 10 0.2a y bx$ ． ∴ $ 0.78 0.2y x ． 取 16x ，得 $ 0.78 16 0.2 12.68y 万元，故选 A ． 【点睛】 本题主要考查线性回归方程的求法，考查了学生的计算能力，属于中档题． 10．C 解析： C 【解析】 【分析】 执行程序框图，可得程序框图的功能是计算并输出分段函数 3 2 , 0 , 0 x xy x x 的值，从而计算 得解 . 【详解】 执行程序框图，可得程序框图的功能是计算并输出分段函数 3 2 , 0 , 0 x xy x x 的值， 由于 2 0x ，可得 2( 2) 4y ，则输出的 y 等于 4，故选 C. 【点睛】 该题考查的是有关程序框图的问题，涉及到的知识点有读取程序框图的输出的结果，在解 题的过程中，需要明确框图的功能，从而求得结果 . 11．A 解析： A 【解析】 【分析】 先列出不超过 11 的素数 ,再列举出随机选取 2 个不同的数的情况 ,进而找到和小于等于 10 的 情况 ,即可求解 【详解】 不超过 11 的素数有 :2,3,5,7,11,共有 5 个 , 随机选取 2 个不同的数可能 为: 2,3 , 2,5 , 2,7 , 2,11 , 3,5 , 3,7 , 3,11 , 5,7 , 5,11 , 7,11 ,共有 10 种情况 , 其中和小于等于 10 的有 : 2,3 , 2,5 , 2,7 , 3,5 , 3,7 ,共有 5 种情况 , 则概率为 5 1 10 2 P = = , 故选 :A 【点睛】 本题考查列举法求古典概型的概率 ,属于基础题 12．C 解析： C 【解析】 【分析】 设小赵到达汽车站的时刻为 x，小王到达汽车站的时刻为 y，根据条件建立二元一次不等式 组，求出对应的区域面积，结合几何概型的概率公式进行计算即可． 【详解】 如图，设小赵到达汽车站的时刻为 x，小王到达汽车站的时刻为 y， 则 0≤x≤15，0≤y≤15， 两人到达汽车站的时刻（ x，y）所对应的区域在平面直角坐标系中画出（如图所示）是大 正方形． 将 2 班车到站的时刻在图形中画出，则两人要想乘同一班车， 必须满足 {（ x，y）| 0 5 0 5 x y ，或 5 15 5 15 x y ＜ ＜ } ， 即（ x，y）必须落在图形中的 2 个带阴影的小正方形内，则阴影部分的面积 S=5×5+10×10=125， 则小赵和小王恰好能搭乘同一班公交车去上学的概率 P= 125 15 15 = 5 9 ， 故选： C 【点睛】 本题主要考查几何概型的概率公式的应用，根据条件求出对应区域的面积是解决本题的关 键． 二、填空题 13．【解析】【分析】确定在正方形的位置即可求解【详解】由题时则当在上 运动时的长度大于 5 故的长度大于 5 的概率等于故答案为【点睛】本题考查长 度型几何概型确定的轨迹是关键是基础题 解析： 1 8 【解析】 【分析】 确定 E 在正方形的位置即可求解 【详解】 由题 3BG DF 时 5AG AF ，则当 E 在 ,GC CF 上运动时， AE 的长度大于 5 故 AE 的长度大于 5 的概率等于 1 1 1 16 8 故答案为 1 8 【点睛】 本题考查长度型几何概型，确定 E 的轨迹是关键，是基础题 14．【解析】由题意可知 2 次检测结束的概率为 3 次检测结束的概率为则恰好 检测四次停止的概率为 解析： 3 5 【解析】 由题意可知， 2 次检测结束的概率为 2 2 2 2 5 1 10 Ap A ， 3 次检测结束的概率为 3 1 1 2 3 2 3 2 3 3 5 3 10 A C C Ap A ， 则恰好检测四次停止的概率为 2 3 1 3 31 1 10 10 5 p p p . 15．【解析】【分析】取圆内接等边三角形的顶点为弦的一个端点当另一端点 在劣弧上时求出劣弧的长度运用几何概型的计算公式即可得结果【详解】记事 件 {弦长超过圆内接等边三角形的边长 }如图取圆内接等边三角形的顶点为 解析： 1 3 【解析】 【分析】 取圆内接等边三角形 BCD 的顶点 B 为弦的一个端点，当另一端点在劣弧 CD 上时， BE BC ，求出劣弧 CD 的长度，运用几何概型的计算公式，即可得结果 . 【详解】 记事件 A { 弦长超过圆内接等边三角形的边长 } ， 如图，取圆内接等边三角形 BCD 的顶点 B 为弦的一个端点， 当另一端点在劣弧 CD 上时， BE BC ， 设圆的半径为 r ，劣弧 CD 的长度是 2 3 r ， 圆的周长为 2 r ， 所以 2 13 2 3 r P A r ，故答案为 1 3 . 【点睛】 本题主要考查“长度型”的几何概型，属于中档题 . 解决几何概型问题常见类型有：长度 型、角度型、面积型、体积型，求与长度有关的几何概型问题关鍵是计算问题的总长度以 及事件的长度；几何概型问题还有以下几点容易造成失分，在备考时要高度关注：（ 1）不 能正确判断事件是古典概型还是几何概型导致错误；（ 2）基本事件对应的区域测度把握不 准导致错误 ；（ 3）利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误 . 16．【解析】试题分析：根据题意正方形的面积为而阴影部分由函数与围成其 面积为则正方形中任取一点点取自阴影部分的概率为则正方形中任取一点点取 自阴影部分的概率为考点：定积分在求面积中的应用几何概型点评 :本题考 解析： 【解析】 试题分析：根据题意，正方形 的面积为 而阴影部分由函数 与 围成，其面积为 ， 则正方形 中任取一点 ,点 取自阴影部分的概率为 . 则正方形中任取一点，点取自阴影部分的概率为 考点：定积分在求面积中的应用 几何概型 点评 :本题考查几何概型的计算，涉及定积分在求面积中的应用，关键是正确计算出阴影部 分的面积 . 17．【解析】分析：先确定总事件数再确定向上的点数是 2 的倍数的事件数最 后根据古典概型概率公式求结果详解：因为投掷一枚均匀的骰子向上的点数有 6 种情况向上的点数是 2 的倍数的事件数为 3 所以概率为点睛：古典概型中 解析： 1 2 【解析】 分析：先确定总事件数，再确定向上的点数是 2 的倍数的事件数，最后根据古典概型概率 公式求结果 . 详解：因为投掷一枚均匀的骰子，向上的点数有 6 种情况，向上的点数是 2 的倍数的事件 数为 3，所以概率为 3 1= 6 2 . 点睛：古典概型中基本事件数的探求方法 (1)列举法 . (2)树状图法：适合于较为复杂的问题中的基本事件的探求 .对于基本事件有 “有序 ”与 “无序 ” 区别的题目，常采用树状图法 . (3)列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题 目具体化 . (4)排列组合法：适用于限制条件较多且元素数目较多的题目 . 18．78【解析】【分析】求得 4 位同学各自在周六周日两天中任选一天参加公 益活动周六周日都有同学参加公益活动的情况利用古典概型概率公式求解即可 【详解】 4位同学各自在周六周日两天中任选一天参加公益活动共有 24 解析： 【解析】 【分析】 求得 4 位同学各自在周六、周日两天中任选一天参加公益活动、周六、周日都有同学参加 公益活动的情况，利用古典概型概率公式求解即可． 【详解】 4 位同学各自在周六、周日两天中任选一天参加公益活动，共有 24=16 种情况， 周六、周日都有同学参加公益活动，共有 24﹣2=16﹣2=14 种情况， ∴所求概率为 = ． 故答案为： ． 【点睛】 有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数： 1．基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏， 可借助“树状图”列举； 2．注意区分排列与组合，以及计数原理的正确使用． 19．【解析】分析：将原问题转化为几何概型的问题然后利用面积型几何概型 公式整理计算即可求得最终结果详解：原问题即已知求的概率其中概率空间为 如图所示的正方形满足题意的部分为图中的阴影部分所示其中结合面积型几 解析： 17 25 【解析】 分析：将原问题转化为几何概型的问题，然后利用面积型几何概型公式整理计算即可求得 最终结果 . 详解：原问题即已知 0 1,0 1x y ，求 4 5 x y 的概率， 其中概率空间为如图所示的正方形，满足题意的部分为图中的阴影部分所示， 其中 4,0 5 E ， 40, 5 F ， 结合面积型几何概型计算公式可得满足题意的概率值为： 1 4 4 172 5 51 1 1 25 p . 点睛：数形结合为几何概型问题的解决提供了简捷直观的解法．用图解题的关键：用图形 准确表示出试验的全部结果所构成的区域，由题意将已知条件转化为事件 A 满足的不等 式，在图形中画出事件 A 发生的区域，据此求解几何概型即可 . 20．1【解析】分析：根据平均数与对应概率乘积的和得总平均数计算结果详解 ：点睛：本题考查平均数考查基本求解能力 解析： 1 【解析】 分析：根据平均数与对应概率乘积的和得总平均数，计算结果 . 详解： 72 45% 74 (1 45%) 72.1 ． 点睛：本题考查平均数，考查基本求解能力 . 三、解答题 21． （1） 3 10 ；（ 2） y 关于 x 的线性回归方程为 $ 13 312．xy ，预测该公司 2019 3Q 的 销售额为 122.2百万元 . 【解析】 【分析】 （1）列举出所有的基本事件，并确定事件“这 2 个季度的销售额都超过 6千万元”然后利 用古典概型的概率公式可计算出所求事件的概率； （2）计算出 x 和 y 的值，然后将表格中的数据代入最小二乘法公式，计算出 b$ 和 $a 的值， 可得出 y 关于 x 的线性回归方程，然后将 7x 代入回归直线方程即可得出该公司 2019 3Q 的销售额的估计值 . 【详解】 （1）从 5个季度的数据中任选 2 个季度，这 2 个季度的销售额有 10种情况： 46 56, 、 46 67, 、 4686, 、 4696, 、 56 67, 、 5686, 、 56 96, 、 67 86, 、 67 96, 、 86 96, 设“这 2 个季度的销售额都超过 6千万元”为事件 A ，事件 A 包含 67 86, 、 67 96, 、 86 96, ， 3种情况，所以 3 10 P A ； （2） 1 2 3 4 5 3 5 x ， 1 46 56 67 86 96 70.2 5 y ， 2 2 2 2 2 2 1 46 2 56 3 67 4 86 5 96 5 3 70.2 130 13 1 2 3 4 5 5 3 12 b$ ， $ $ 31.2a y bx$ . 所以 y 关于 x 的线性回归方程为 $ 13 312．xy ， 令 7x ，得 $ 13 7 312 122.2．y （百万元） 所以预测该公司 2019 3Q 的销售额为 122.2百万元． 【点睛】 本题考查利用古典概型的概率公式计算事件的概率，同时也考查了利用最小二乘法求回归 直线方程，同时也考查了回归直线方程的应用，考查计算能力，属于中等题 . 22． （1） 0.005a （2）平均数为 73，中位数为： 271 3 . 【解析】 【分析】 （1）由频率和为 1 求解即可； （2）以各区间中点值代表各组的取值 ,进而求得平均数；求出从左边开始小矩形的面积的 和为 0.5 对应的横轴的值即为中位数 【详解】 （1）由频率分布直方图知 2 0.02 0.03 0.04 10 1a , 解得 0.005a （2）估计这 100 名学生语文成绩的平均分为 : 55 0.005 10 65 0.04 10 75 0.03 10 85 0.02 10 95 0.005 10 73 由（ 1）, 设中位数为 x , 则 0.005 10 0.04 10 0.03 70 0.5x 解得 271 3 x , 故估计中位数为： 271 3 . 【点睛】 本题考查频率的性质 ,考查利用频率分布直方图求平均数和中位数 ,考查数据处理能力 23． (1) 2 2 , 0 log ,0 4 2 , 4x x x y x x x 当 0x 时， y 无解 .(2) 2x . 【解析】 【分析】 (1)根据框图得到函数解析式；（ 2）结合第一问得到的函数表达式，分情况得到 x 值即可 . 【详解】 （1）函数解析式为 2 2 , 0 log ,0 4 2 , 4x x x y x x x ， 当 0x 时， y 无解 . （2）当 0x 时， 2 4x ， 2x 或 2 （舍） . 当 0 4x 时， 2log 4x ，解得 16x （舍） . 当 4x 时， 2 4x ，解得 2x （舍） 所以 2x 【点睛】 这个题目考查了程序框图的应用，以及分段函数的应用；解决分段函数求值问题的策略： (1)在求分段函数的值 f(x0)时，一定要首先判断 x0 属于定义域的哪个子集，然后再代入相应 的关系式； (2)分段函数是指自变量在不同的取值范围内，其对应法则也不同的函数，分段 函数是一个函数，而不是多个函数；分段函数的定义域是各段定义域的并集，值域是各段 值域的并集，故解分段函数时要分段解决； (3)求 f(f(f(a)))的值时，一般要遵循由里向外逐 层计算的原则 . 24．（1） 0.9 ；（ 2） 0.085a ， 0.125b ；（ 3）第 4 组 . 【解析】 试题分析：（ 1）由频率分布表知， 100 人中有 10 人阅读时间不少于 12 小时，所以由对立 事件的概率计算公式得 p= ；（ 2）由频率分表知，阅读时间在 [4，6）的共 17 人，所以样本落在该组的概率为 0．17，则频率分布直方图中样本落在 [4，6）的小矩形的 面积为 0．17，从而求出矩形的高即 a 的值，同理得到 b 的值；（ 3）可以通过频率分布表 或频率分布直方图求出平均数即可知平均数在那一组． 试题解析：（ 1）根据频数分布表， 100 名学生中课外阅读时间不少于 12 小时的学生共有 6+2+2=10 名，所以样本中的学生课外阅读时间少于 12 小时的频率是 ； （2）课外阅读时间落在 [4，6）的有 17 人，频率为 0．17，所以 ， 课外阅读时间落在 [8， 10）的有 25 人，频率为 0． 25，所以 ， （3）估计样本中的 100 名学生课外阅读时间的平均数在第 4 组． 考点：频率分布表和频率分布直方图的应用． 【方法点睛】频率分布直方图的几个常用结论：（ 1）所有小矩形的面积和为 1；（ 2）小 矩形的高等于样本落在该组的概率除以组距；（ 3）最高的小矩形的所在组的区间的中点值 即为众数；（ 4）每个组的区间中点值乘以所在组的概率之和即为平均数；（ 4）样本取值 m，两侧的样本数据的概率相等且为 ，则 m 即为中位数． 25． （1） 1 20 （ 2）68 66.67（3）120 【解析】 【分析】 （1）根据共有 800 个学生，抽取 40 个学生的成绩可知，每个学生成绩被抽取的机会均 等，即可计算（ 2）由各组的频率和等于 1 直接列式计算成绩在 [80，90）的学生频率，再 估计这次月考数学成绩的平均分和中位数（ 3）由频率直方图可知成绩 80 分以上的频率， 即可计算全年级 80 分以上的人数 . 【详解】 （1）根据共有 800 个学生，抽取 40 个学生的成绩，每个学生成绩被抽取的机会均等，故 40 1 800 20 P （2）由频率分布直方图得成绩在区间 [80，90）内的频率为： 1-（0.005+0.015+0.045+0.020+0.005 ）×10=0.1， 所以平均分 =0.05×45+0.15×55+0.45×65+0.20×75+0.10×85+0.05×95=68 由频率分布直方图得： [40，60）的频率为：（ 0.005+0.015）×10=0.2， [60，70）的频率为： 0.045 ×10=0.45， ∴估计这 40 名学生成绩的中位数为： 0.5 0.260 10 66.67 0.45 （3）由（ 1）及频率分布直方图可知，学生成绩 80 分以上的频率为： 0.1+0.05=0.15 ， 故地理考试全年级 80 分以上的人数为 800 0.15 120人. 【点睛】 本题主要考查了频数、平均数、中位数的估计，考查频率分布直方图的性质等基础知识， 考查运算求解能力，属于中档题． 26． （Ⅰ） 3 10 ；（Ⅱ） 7 10 . 【解析】 【分析】 列举出所有的基本事件 ,共有 20 个, （I）从中查出第一次取到二等品 ,且第二次取到的是一 等品的基本事件数共有 6 个,利用古典概型的概率公式可得结果；（ II ）事件 “至少有一次取 到二等品 ”的对立事件是 “取到的全是一等品 ”, “取到的全是一等品 ”包括了 6 个事件， “至少 有一次取到二等品 ”取法有 14 种 , 利用古典概型的概率公式可得结果 . 【详解】 （I ）令 3 只一等品灯泡分别为 , ,a b c ；2 只二等品灯泡分别为 ,X Y . 从中取出 2 只灯泡，所有的取法有 20 种，分别为： , , , , , , , , , , , , , , , , ,a b a c a X a Y b a b c b X b Y c a ，， ,c X ， ,c Y ， ,X a ， ,X b ， ,X c ， ,X Y ， ,Y a ， ,Y b ， ,Y c ， ,Y X 第一次取到二等品，且第二次取到的是一等品取法有 6 种， 分别为 , , , , , , , , , , ,X a X b X c Y a Y b Y c ，故概率是 6 3 20 10 ； （II ）事件“至少有一次取到二等品”的对立事件是“取到的全是一等品”， “取到的全是一等品”包括了 6 种分别为 , , , , , , , , , , ,a b a c b a b c c a c b ， 故“至少有一次取到二等品”取法有 14 种 , 事件“至少有一次取到二等品”的概率是 14 7 20 10 . 【点睛】 本题主要考查古典概型概率公式的应用，属于基础题，利用古典概型概率公式求概率时， 找准基本事件个数是解题的关键，基本亊件的探求方法有 ，(1) 枚举法：适合给定的基本事 件个数较少且易一一列举出的； (2) 树状图法：适合于较为复杂的问题中的基本亊件的探求 . 在找基本事件个数时，一定要按顺序逐个写出：先 1 1( , )A B ， 1 2( , )A B ⋯ . 1( , )nA B ，再 2 1( , )A B ， 2 2( , )A B ⋯ .. 2( , )nA B 依次 3 1( , )A B 3 2( , )A B ⋯. 3( , )nA B ⋯ 这样才能避免多写、 漏写现象的发生 .