【数学】2020届一轮复习人教A版第二章第5节指数与指数函数学案 16页

第5节　指数与指数函数 最新考纲　1.了解指数函数模型的实际背景；2.理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算；3.理解指数函数的概念及其单调性，掌握指数函数图象通过的特殊点，会画底数为2，3，10，，的指数函数的图象；4.体会指数函数是一类重要的函数模型.‎ 知 识 梳 理 ‎1.根式 ‎(1)概念：式子叫做根式，其中n叫做根指数，a叫做被开方数.‎ ‎(2)性质：()n＝a(a使有意义)；当n为奇数时，＝a，当n为偶数时，＝|a|＝ ‎2.分数指数幂 ‎(1)规定：正数的正分数指数幂的意义是a＝(a>0，m，n∈N*，且n>1)；正数的负分数指数幂的意义是a－＝(a>0，m，n∈N*，且n>1)；0的正分数指数幂等于0；0的负分数指数幂没有意义.‎ ‎(2)有理指数幂的运算性质：aras＝ar+s；(ar)s＝ars；(ab)r＝arbr，其中a>0，b>0，r，s∈Q.‎ ‎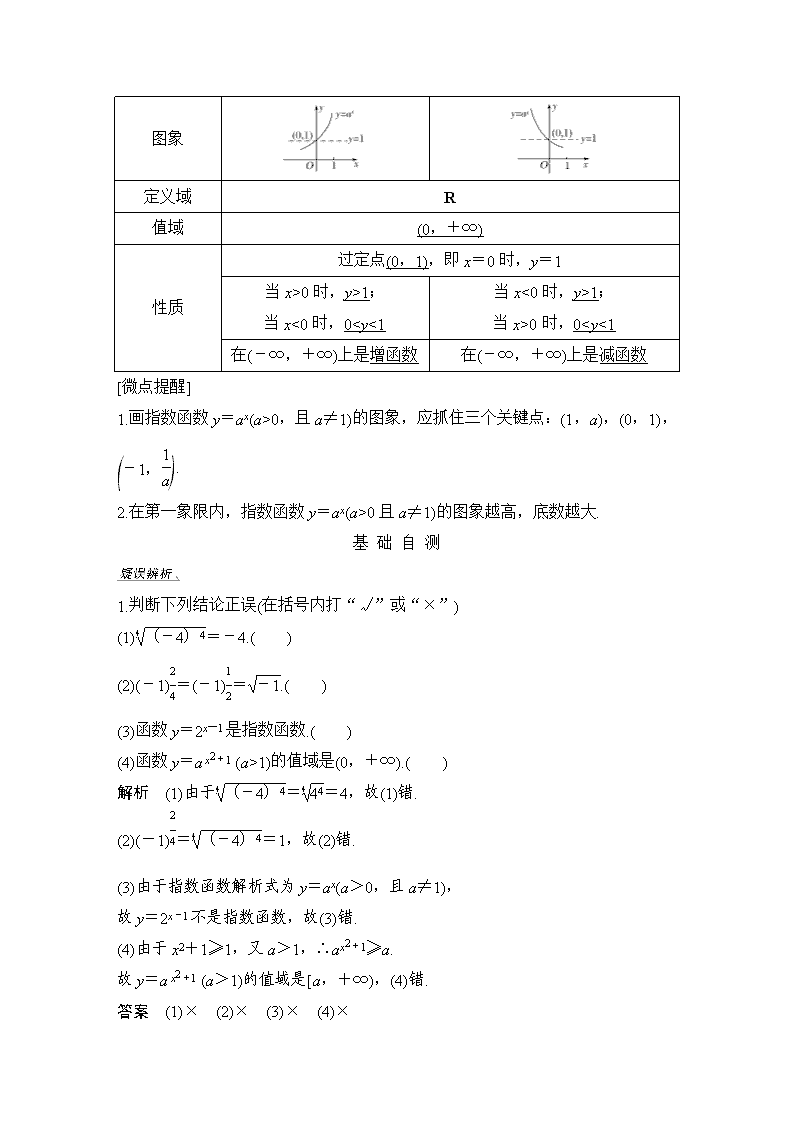3.指数函数及其性质 ‎(1)概念：函数y＝ax(a>0且a≠1)叫做指数函数，其中指数x是自变量，函数的定义域是R，a是底数.‎ ‎(2)指数函数的图象与性质 a>1‎ ‎00时，y>1；‎ 当x<0时，01；‎ 当x>0时，00，且a≠1)的图象，应抓住三个关键点：(1，a)，(0，1)，.‎ ‎2.在第一象限内，指数函数y＝ax(a>0且a≠1)的图象越高，底数越大.‎ 基 础 自 测 ‎1.判断下列结论正误(在括号内打“√”或“×”)‎ ‎(1)＝－4.(　　)‎ ‎(2)(－1)＝(－1)＝.(　　)‎ ‎(3)函数y＝2x－1是指数函数.(　　)‎ ‎(4)函数y＝a x2＋1 (a>1)的值域是(0，＋∞).(　　)‎ 解析　(1)由于＝＝4，故(1)错.‎ ‎(2)(－1)＝＝1，故(2)错.‎ ‎(3)由于指数函数解析式为y＝ax(a＞0，且a≠1)，‎ 故y＝2x－1不是指数函数，故(3)错.‎ ‎(4)由于x2＋1≥1，又a＞1，∴ax2＋1≥a.‎ 故y＝a x2＋1 (a＞1)的值域是[a，＋∞)，(4)错.‎ 答案　(1)×　(2)×　(3)×　(4)×‎ ‎2.(必修1P56例6改编)若函数f(x)＝ax(a>0，且a≠1)的图象经过，则 f(－1)＝(　　)‎ A.1 B.2 C. D.3‎ 解析　依题意可知a2＝，解得a＝，‎ 所以f(x)＝，所以f(－1)＝＝.‎ 答案　C ‎3.(必修1P59A6改编)某种产品的产量原来是a件，在今后m年内，计划使每年的产量比上一年增加p%，则该产品的产量y随年数x变化的函数解析式为(　　)‎ A.y＝a(1＋p%)x(00，将表示成分数指数幂，其结果是(　　)‎ A.a B.a C.a D.a 解析　由题意得＝a2－－＝a.‎ 答案　C ‎5.(2017·北京卷)已知函数f(x)＝3x－，则f(x)(　　)‎ A.是偶函数，且在R上是增函数 B.是奇函数，且在R上是增函数 C.是偶函数，且在R上是减函数 D.是奇函数，且在R上是减函数 解析　函数f(x)的定义域为R，‎ f(－x)＝3－x－＝－3x＝－f(x)，‎ ‎∴函数f(x)是奇函数.‎ 又y＝3x在R上是增函数，函数y＝在R上是减函数，‎ ‎∴函数f(x)＝3x－在R上是增函数.‎ 答案　B ‎6.(2019·福州检测)设a＝0.60.6，b＝0.61.5，c＝1.50.6，则a，b，c的大小关系是(　　)‎ A.a1，∴b0，b>0).‎ 解　(1)原式＝1＋×－ ‎＝1＋×－＝1＋－＝.‎ ‎(2)原式＝＝a+-1＋b1+-2-＝.‎ 规律方法　1.指数幂的运算首先将根式、分数指数幂统一为分数指数幂，以便利用法则计算，但应注意：(1)必须同底数幂相乘，指数才能相加；(2)运算的先后顺序.‎ ‎2.当底数是负数时，先确定符号，再把底数化为正数.‎ ‎3.运算结果不能同时含有根号和分数指数，也不能既有分母又含有负指数.‎ ‎【训练1】 化简下列各式：‎ ‎(1)[(0.064)－2.5]－－π0；‎ ‎(2)a·b－2·÷.‎ 解　(1)原式＝－－1‎ ‎＝－－1‎ ‎＝－－1＝0.‎ ‎(2)原式＝－a－b－3÷ ‎＝－a－b－3÷(ab－)＝－a－·b－ ‎＝－·＝－.‎ 考点二　指数函数的图象及应用 ‎【例2】 (1)(2019·衡水中学检测)不论a为何值，函数y＝(a－1)2x－恒过定点，则这个定点的坐标是(　　)‎ A. B. C. D. ‎(2)若函数f(x)＝|2x－2|－b有两个零点，则实数b的取值范围是________.‎ 解析　(1)y＝(a－1)2x－＝a－2x，令2x－＝0，得x＝－1，故函数y＝(a－1)2x－恒过定点.‎ ‎(2)在同一平面直角坐标系中画出y＝|2x－2|与y＝b的图象，如图所示.‎ ‎∴当01，b<0‎ B.a>1，b>0‎ C.00‎ D.01.73 B.0.6－1>0.62‎ C.0.8－0.1>1.250.2 D.1.70.3<0.93.1‎ ‎(2)设函数f(x)＝若f(a)<1，则实数a的取值范围是________.‎ 解析　(1)A中，∵函数y＝1.7x在R上是增函数，2.5<3，‎ ‎∴1.72.5<1.73，错误；‎ B中，∵y＝0.6x在R上是减函数，－1<2，‎ ‎∴0.6－1>0.62，正确；‎ C中，∵(0.8)－1＝1.25，‎ ‎∴问题转化为比较1.250.1与1.250.2的大小.‎ ‎∵y＝1.25x在R上是增函数，0.1<0.2，‎ ‎∴1.250.1<1.250.2，即0.8－0.1<1.250.2，错误；‎ D中，∵1.70.3>1, 0<0.93.1<1，‎ ‎∴1.70.3>0.93.1，错误.‎ ‎(2)当a<0时，原不等式化为－7<1，‎ 则2－a<8，解之得a>－3，所以－30，且a≠1)在区间[－1，1]上的最大值是14，则a的值为________.‎ 解析　令ax＝t，则y＝a2x＋2ax－1＝t2＋2t－1＝(t＋1)2－2.当a>1时，因为x∈‎ ‎[－1，1]，所以t∈，又函数y＝(t＋1)2－2在上单调递增，所以ymax＝(a＋1)2－2＝14，解得a＝3(负值舍去).当01且a≠2)在区间(0，＋∞)上具有不同的单调性，则M＝(a－1)0.2与N＝的大小关系是(　　)‎ A.M＝N B.M≤N C.MN ‎(2)函数f(x)＝的单调递增区间为________，单调递减区间为________.‎ ‎(3)已知函数f(x)＝b·ax(其中a，b为常量，且a>0，a≠1)的图象经过点A(1，6)，B(3，24).若不等式＋－m≥0在x∈(－∞，1]上恒成立，则实数m的最大值为________.‎ 解析　(1)因为f(x)＝x2－a与g(x)＝ax(a>1，且a≠2)在(0，＋∞)上具有不同的单调性.‎ 所以a>2.‎ 因此M＝(a－1)0.2>1，N＝<1.‎ 故M>N.‎ ‎(2)依题意知x2－5x＋4≥0，解得x≥4或x≤1，令u＝＝，x∈(－∞，1]∪[4，＋∞)，所以当x∈(－∞，1]时，u是减函数，当x∈[4，＋∞)时，u是增函数.而3>1，所以由复合函数的单调性可知，f(x)＝在区间(－∞，1]上是减函数，在区间[4，＋∞)上是增函数.‎ ‎(3)把A(1，6)，B(3，24)代入f(x)＝b·ax，得结合a>0，且a≠1，解得所以f(x)＝3·2x.要使＋≥m在区间(－∞，1]上恒成立，‎ 只需保证函数y＝＋在区间(－∞，1]上的最小值不小于m即可.因为函数y＝＋在区间(－∞，1]上为减函数，所以当x＝1时，y＝＋有最小值.所以只需m≤即可.所以m的最大值为.‎ 答案　(1)D　(2)[4，＋∞)　(－∞，1]　(3) ‎[思维升华]‎ ‎1.‎ 根式与分数指数幂的实质是相同的，分数指数幂与根式可以互化，通常利用分数指数幂进行根式的化简运算.‎ ‎2.判断指数函数图象上底数大小的问题，可以先通过令x＝1得到底数的值再进行比较.‎ ‎3.指数函数的单调性取决于底数a的大小，当底数a与1的大小关系不确定时应分01两种情况分类讨论.‎ ‎[易错防范]‎ ‎1.对与复合函数有关的问题，要弄清楚复合函数由哪些基本初等函数复合而成，并且一定要注意函数的定义域.‎ ‎2.对可化为a2x＋b·ax＋c＝0或a2x＋b·ax＋c≥0(≤0)形式的方程或不等式，常借助换元法解题，但应注意换元后“新元”的范围.‎ 基础巩固题组 ‎(建议用时：40分钟)‎ 一、选择题 ‎1.(2019·永州模拟)下列函数中，与函数y＝2x－2－x的定义域、单调性与奇偶性均一致的是(　　)‎ A.y＝sin x B.y＝x3‎ C.y＝ D.y＝log2x 解析　y＝2x－2－x是定义域为R的单调递增函数，且是奇函数.而y＝sin x不是单调递增函数，不符合题意；y＝是非奇非偶函数，不符合题意；‎ y＝log2x的定义域是(0，＋∞)，不符合题意；‎ y＝x3是定义域为R的单调递增函数，且是奇函数符合题意.‎ 答案　B ‎2.函数y＝ax－(a>0，且a≠1)的图象可能是(　　)‎ 解析　若a>1时，y＝ax－在R上是增函数，‎ 当x＝0时，y＝1－∈(0，1)，A，B不满足.‎ 若00，a≠1)的图象恒过点A，下列函数中图象不经过点A的是(　　)‎ A.y＝ B.y＝|x－2|‎ C.y＝2x－1 D.y＝log2(2x)‎ 解析　f(x)过定点A(1，1)，将点A(1，1)代入四个选项，y＝的图象不过点A(1，1).‎ 答案　A ‎4.设x>0，且10时，11.‎ 又x>0时，bx0时，>1.‎ ‎∴>1，∴a>b，∴10，且a≠1)，满足f(1)＝，则f(x)的单调递减区间是(　　)‎ A.(－∞，2] B.[2，＋∞)‎ C.[－2，＋∞) D.(－∞，－2]‎ 解析　由f(1)＝，得a2＝，解得a＝或a＝－(舍去)，即f(x)＝.‎ 由于y＝|2x－4|在(－∞，2]上单调递减，在[2，＋∞)上单调递增，‎ 所以f(x)在(－∞，2]上单调递增，在[2，＋∞)上单调递减.‎ 答案　B 二、填空题 ‎6.化简＝________.‎ 解析　原式＝ ‎＝a－－－·b＋－＝.‎ 答案　 ‎7.函数y＝－＋1在区间[－3，2]上的值域是________.‎ 解析　令t＝，因为x∈[－3，2]，所以t∈，故y＝t2－t＋1＝＋.当t＝时，ymin＝；当t＝8时，ymax＝57.故所求函数的值域为.‎ 答案　 ‎8.设偶函数g(x)＝a|x+b|在(0，＋∞)上单调递增，则g(a)与g(b－1)的大小关系是________.‎ 解析　由于g(x)＝a|x+b|是偶函数，知b＝0，‎ 又g(x)＝a|x|在(0，＋∞)上单调递增，得a>1.‎ 则g(b－1)＝g(－1)＝g(1)，‎ 故g(a)>g(1)＝g(b－1).‎ 答案　g(a)>g(b－1)‎ 三、解答题 ‎9.已知函数f(x)＝，a为常数，且函数的图象过点(－1，2).‎ ‎(1)求a的值；‎ ‎(2)若g(x)＝4－x－2，且g(x)＝f(x)，求满足条件的x的值.‎ 解　(1)由已知得＝2，解得a＝1.‎ ‎(2)由(1)知f(x)＝，‎ 又g(x)＝f(x)，则4－x－2＝，‎ ‎∴－－2＝0，‎ 令＝t，则t>0，t2－t－2＝0，即(t－2)(t＋1)＝0，‎ 又t>0，故t＝2，即＝2，解得x＝－1，‎ 故满足条件的x的值为－1.‎ ‎10.(2018·长沙一中月考)已知函数f(x)＝为奇函数.‎ ‎(1)求a的值；‎ ‎(2)判断函数f(x)的单调性，并加以证明.‎ 解　(1)因为函数f(x)是奇函数，且f(x)的定义域为R；所以f(0)＝＝0，所以a＝－1.‎ ‎(2)由(1)知f(x)＝＝1－，函数f(x)在定义域R上单调递增.‎ 证明：设x10，函数f(x)＝的图象经过点P，Q.若2p+q＝36pq，则a＝________.‎ 解析　因为f(x)＝＝，且其图象经过点P，Q，‎ 则f(p)＝＝，即＝－，①‎ f(q)＝＝－，即＝－6，②‎ ‎①×②得＝1，则2p＋q＝a2pq＝36pq，‎ 所以a2＝36，解得a＝±6，因为a>0，所以a＝6.‎ 答案　6‎ ‎14.已知定义在R上的函数f(x)＝2x－，‎ ‎(1)若f(x)＝，求x的值；‎ ‎(2)若2tf(2t)＋mf(t)≥0对于t∈[1，2]恒成立，求实数m的取值范围.‎ 解　(1)当x<0时，f(x)＝0，故f(x)＝无解；‎ 当x≥0时，f(x)＝2x－，‎ 由2x－＝，得2·22x－3·2x－2＝0，‎ 将上式看成关于2x的一元二次方程，‎ 解得2x＝2或2x＝－，‎ 因为2x>0，所以2x＝2，所以x＝1.‎ ‎(2)当t∈[1，2]时，2t＋m≥0，‎ 即m(22t－1)≥－(24t－1)，因为22t－1>0，‎ 所以m≥－(22t＋1)，‎ 因为t∈[1，2]，所以－(22t＋1)∈[－17，－5]，‎ 故实数m的取值范围是[－5，＋∞).‎