- 924.50 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
永州市2020年高考第二次模拟考试试卷
数学(理科)
注意事项:
1.全部答案在答题卡上完成,答在本试题卷上无效。
2.考试结束后,只交答题卡。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设复数z满足,则z的共轭复数为
A.1-i B.1+i C.-1+i D.-1-i
2.已知集合A={x|x<3},B={x|log2x>0},则
A.A∩B={x|11}
3.执行右图所示程序框图,若输入p=,则输出结果为
A.2 B.3 C.4 D.5
4.为了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重情况如三维饼图(1)所示,经过四个月的健身后,他们的体重情况如三维饼图(2)所示。
对比健身前后,关于这20名肥胖者,下面结论不正确的是
A.他们健身后,体重在区间[90kg,100kg)内的人数不变
B.他们健身后,体重在区间[100kg,110kg)内的人数减少了4人
C.他们健身后,这20位健身者体重的中位数位于[90kg,100kg)
D.他们健身后,原来体重在[110kg,120kg]内的肥胖者体重都至少减轻了10kg
5.已知数列是首项为8,公比为的等比数列,则a4等于
A.8 B.32 C.64 D.128
6.某校高三年级有男生220人,编号为1,2,…,220;姓380人,编号为221,222,…,600。为了解学生的学习状态,按编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查,第一组抽到的号码为10。现从这10名学生中随机抽取2人进行座谈,则这2人中既有男生又有女生的概率是
A. B. C. D.
7.已知定义在R上的奇函数f(x)满足f(x+1)+f(3-x)=0,若f(1)=2,则f(1)+f(2)+f(3)+…+f(2019)=
A.-2 B.0 C.2 D.2020
8.已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<π)的部分图像如右图所示,且A(,-l),B(π,1),则φ的值为
A.- B. C.- D.
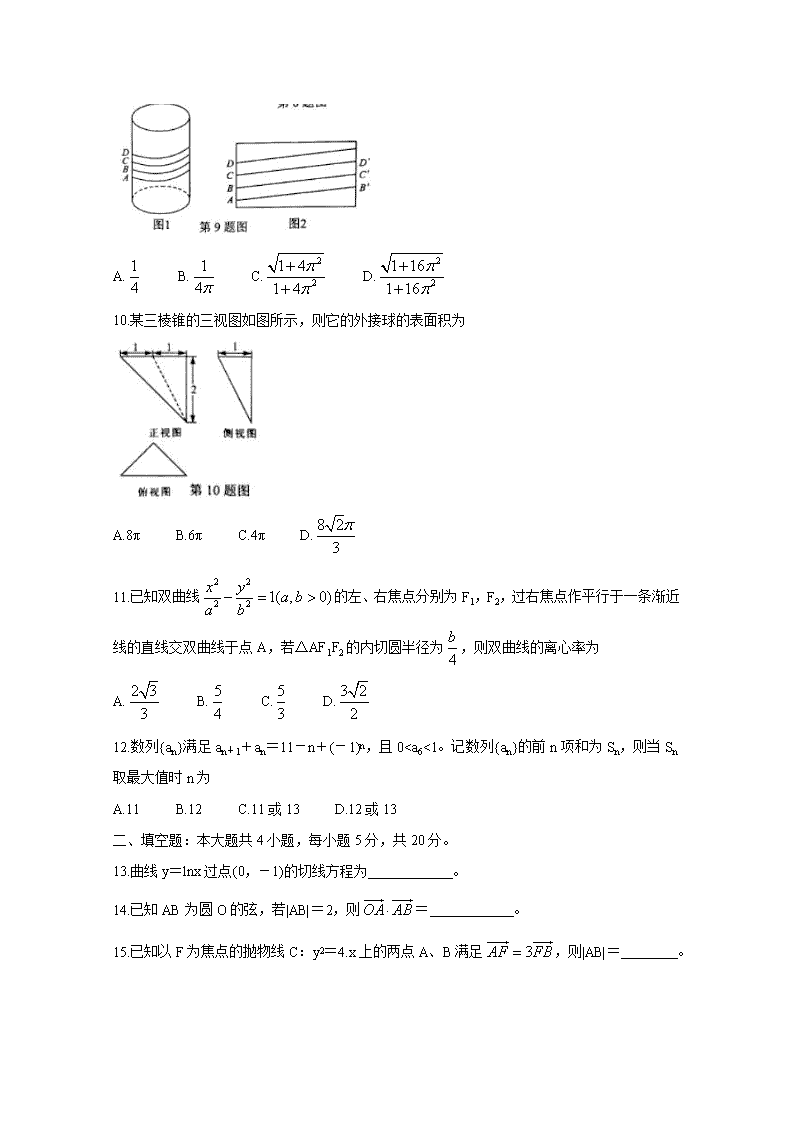
9.北方的冬天户外冰天雪地,若水管裸露在外,则管内的水就会结冰从而冻裂水管,给用户生活带来不便。每年冬天来临前,工作人员就会给裸露在外的水管“保暖”:在水管外面包裹保温带,用一条保温带盘旋而上一次包裹到位。某工作人员采用四层包裹法(除水管两端外包裹水管的保温带都是四层):如图1所示是相邻四层保温带的下边缘轮廓线,相邻两条轮廓线的间距是带宽的四分之一。设水管的直径与保温带的宽度都为4cm。在图2水管的侧面展开图中,此保温带的轮廓线与水管母线所成的角的余弦值是(保温带厚度忽略不计)
A. B. C. D.
10.某三棱锥的三视图如图所示,则它的外接球的表面积为
A.8π B.6π C.4π D.
11.已知双曲线的左、右焦点分别为F1,F2,过右焦点作平行于一条渐近线的直线交双曲线于点A,若△AF1F2的内切圆半径为,则双曲线的离心率为
A. B. C. D.
12.数列{an}满足an+1+an=11-n+(-1)n,且00)与C1,C2分别交于点M、N,求的最大值。
23.[选修4-5:不等式选讲](本题满分10分)
已知函数f(x)=|x-2|。
(1)求不等式f(x)≤2x+5的解集;
(2)记函数g(x)=f(x+1)-f(-x+5),且g(x)的最大值为M,若a>0,求证:。
永州市2020年高考第二次模拟考试试卷
数学(理科)参考答案
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
C
C
B
D
B
A
C
C
二、填空题:本大题共4小题,每小题5分,共20分. 把答案填在答题卡中对应题号后的横线上.
13. 14. 15.
16.(1)(2分); (2) (3分)
三、解答题:本大题共70分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)解:(1)
…………………………………………………………………3分
在中,由余弦定理可得
………………………………………………………………6分
(2)
……8分
,,
,,
………………………………………………………10分
在中,由正弦定理可得,
. ………………………………………………12分
18.(本小题满分12分)
A
B
C
F
E
D
(第18题图)
x
y
解:(1)证明:因为,,
所以,因为,所以.
又因为,,
所以,而,
所以,又,
所以. ………………6分
(2)解:设直线与平面所成交的余弦值为.
连接,在中,,,
,所以,且,,
又因为,,,
所以,.在中,,,所以.
如图,以点为坐标原点,分别以 为x,y,z轴建立空间直角坐标系,各点
坐标为,,,,
因为,为的中点,所以为的中点,即,
设平面的法向量,
,,
由,即,
整理得, 令,得,,则.……10分
因为 ,所以,
故直线与平面所成交的正弦值为. ……………12分
19.(本小题满分12分)解:(1)椭圆过点,∴,① ………2分
又因为直线的斜率之积为,可求得,②
联立①②得.
∴所求的椭圆方程为. ……………………………………………6分
(2)方法1:由(1)知,. 由题意可设,
令x=m,得.又设
由整理得:.…………………6分
∵,∴,,
所以, ……………………………………………………8分
∴ ,…10分
要使与k无关,只须,此时恒等于4.
∴ ……………………………………………………………………………12分
方法2::设,则,令x=m,得,
∴
由有,
所以,
要使与无关,只须,此时.
∴ …………………………………………………………………………12分
20.(本小题满分12分)
解:(1)如果,采用逐份检验方式,设检测结果恰有两份次品的概率为
检测结果恰有两份次品的概率. ………………………3分
(2)记采用逐份检验方式,样本需要检验的总次数为,采用混合检验方式,样本需要检验的总次数为,由已知得,的所有可能取值为
,
= …………………5分
要减少检验次数,则,则
∴,,即, ………………………7分
(3)①两组采用混合检验的检验次数分别为,,则由(2)知,
, ,
………………10分
②设这组采用混合检验的检验次数分别为,,, ,,,且检验总次数,
,
,
所以检验总次数的数学期望. …………………12分
21.(本小题满分12分)
证明:(1)当x∈(0,1)时,f′(x)=>0,函数f(x)在(0,1)上为增函数.又f(0)=-e+1<0,f(1)=3>0,所以存在唯一x0∈(0,1),使f(x0)=0.…4分
(2) 当x∈(1,2)时,,
令t=2-x, x=2-t,x∈(1,2),t∈(0,1),
, t∈(0,1) ……………………6分
记函数,t∈(0,1).
则h′(t)=. ……………………8分
由(1)得,当t∈(0,x0)时,f(t)<0,h′(t)>0,
当t∈(x0,1)时,f(t) >0,h′(t) <0.
故在(0,x0)上h(t)是增函数,又h(0)=0,从而可知当t∈(0,x0]时,h(t)>0,所以h(t)在(0,x0]上无零点.
在(x0,1)上h(t)为减函数,由h(x0)>0,h(1)=-ln 2<0,知存在唯一t1∈(x0,1),使h(t1)=0, ……………………………………………10分
故存在唯一的t1∈(0,1),使h(t1)=0.
因此存在唯一的x1=2-t1∈(1,2),使g(x1)=g(2-t1)=h(t1)=0.
因为当t∈ (0,1)时,1+t>0,故与g(2-t)有相同的零点,所以存在唯一的x1∈(1,2),使g(x1)=0.
因为x1=2-t1,t1>x0,所以x0+x1<2. …………………………………………12分
22.(本小题满分10分)
解:(1)直线的直角坐标方程为,
将,代入方程得
,即, …………………………5分
(2)设直线的极坐标方程为,设,
则,
由,有,
当时,的最大值为. ………………………10分
23.(本小题满分10分)
解:(1)由得,解得
不等式的解集为. ………………………5分
(2)
当且仅当时等号成立,
, ………………………7分
.
当且仅当,即时等号成立. ………………………10分