2021版高考数学一轮复习核心素养测评四十六平行关系理北师大版 9页

核心素养测评四十六 平行关系 ‎(30分钟　60分)‎ 一、选择题(每小题5分,共25分)‎ ‎1.已知直线a,b,平面α,β,aα,bα,则a∥β,b∥β是α∥β的 ‎ ‎(　　)‎ A.充分但不必要条件 B.必要但不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎【解析】选B.因为直线a,b不一定相交,所以a∥β,b∥β时α,β不一定平行,而α∥β时平面α内任意直线都平行平面β,即a∥β,b∥β,因此a∥β,b∥β是α∥β的必要但不充分条件.‎ ‎2.给出下列关于互不相同的直线l,m,n和平面α,β,γ的三个命题:‎ ‎①若l与m为异面直线,lα,mβ,则α∥β;‎ ‎②若α∥β,lα,mβ,则l∥m;‎ ‎③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.‎ 其中真命题的个数为 (　　)‎ A.3 B.2 C.1 D.0‎ ‎【解析】选C.①中当α与β不平行时,也可能存在符合题意的l,m.‎ ‎②中l与m也可能异面.‎ ‎③中⇒l∥m,‎ 同理l∥n,则m∥n,正确.‎ ‎3.如图是正方体的平面展开图,则在这个正方体中,下列判断正确的是 (　　)‎ A.平面BME∥平面ACN B.AF∥CN - 9 -‎ C.BM∥平面EFD D.BE与AN相交 ‎【解析】选A.作出如图所示的正方体.易知AN∥BM,AC∥EM,所以AN∥平面BEM,AC∥平面BEM,又AN∩AC=A,所以平面ACN∥平面BEM.‎ ‎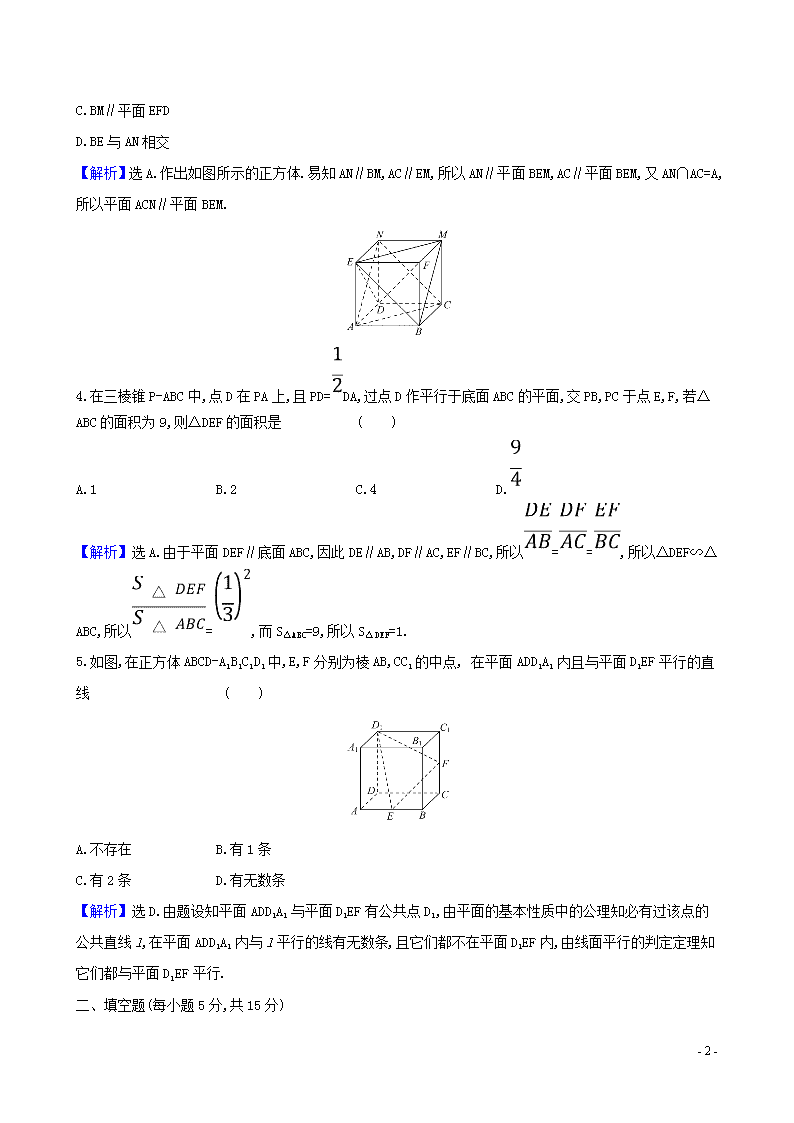4.在三棱锥P-ABC中,点D在PA上,且PD=DA,过点D作平行于底面ABC的平面,交PB,PC于点E,F,若△ABC的面积为9,则△DEF的面积是 (　　)‎ A.1 B.2 C.4 D.‎ ‎【解析】选A.由于平面DEF∥底面ABC,因此DE∥AB,DF∥AC,EF∥BC,所以==,所以△DEF∽△ABC,所以=,而S△ABC=9,所以S△DEF=1.‎ ‎5.如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点, 在平面ADD1A1内且与平面D1EF平行的直线 (　　)‎ A.不存在 B.有1条 C.有2条 D.有无数条 ‎【解析】选D.由题设知平面ADD1A1与平面D1EF有公共点D1,由平面的基本性质中的公理知必有过该点的公共直线l,在平面ADD1A1内与l平行的线有无数条,且它们都不在平面D1EF内,由线面平行的判定定理知它们都与平面D1EF平行.‎ 二、填空题(每小题5分,共15分)‎ - 9 -‎ ‎6.如图所示,CD,AB均与平面EFGH平行,E,F,G,H分别在BD,BC,AC,AD上,且CD⊥AB.则四边形EFGH的形状为________________. ‎ ‎【解析】因为CD∥平面EFGH,‎ 而平面EFGH∩平面BCD=EF,所以CD∥EF.‎ 同理HG∥CD,所以EF∥HG.‎ 同理HE∥GF,所以四边形EFGH为平行四边形.‎ 又因为CD⊥AB,所以HE⊥EF,‎ 所以平行四边形EFGH为矩形.‎ 答案:矩形 ‎7.已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于A,C,过点P的直线n与α,β分别交于B,D且PA=6,AC=9,PD=8,则BD的长为________________. ‎ ‎【解析】根据题意可得到如图两种情况:‎ 可求出BD的长分别为或24.‎ 答案:24或 ‎8.α,β是两个平面,m,n是两条直线,有下列四个命题:‎ ‎①如果m⊥n,m⊥α,n∥β,那么α⊥β;‎ ‎②如果m⊥α,n∥α,那么m⊥n;‎ ‎③如果α∥β,mα,那么m∥β;‎ ‎④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.‎ 其中正确的命题有________________.(填写所有正确命题的序号) ‎ - 9 -‎ ‎【解析】当m⊥n,m⊥α,n∥β时,两个平面的位置关系不确定,故①错误,经判断知②③④均正确,故正确命题为②③④.‎ 答案:②③④‎ 三、解答题(每小题10分,共20分)‎ ‎9.如图,在直三棱柱ABC-A1B1C1中,点M,N分别为线段A1B,AC1的中点.‎ 求证:MN∥平面BB1C1C.‎ ‎【证明】如图,连接A1C.在直三棱柱ABC-A1B1C1中,侧面AA1C1C为平行四边形.‎ 又因为N为线段AC1的中点,‎ 所以A1C与AC1相交于点N,‎ 即A1C经过点N,且N为线段A1C的中点.‎ 因为M为线段A1B的中点,所以MN∥BC.‎ 又因为MN⊈平面BB1C1C,BC平面BB1C1C,‎ 所以MN∥平面BB1C1C.‎ ‎10.如图,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC,SC的中点,求证: ‎ ‎(1)直线EG∥平面BDD1B1.‎ ‎(2)平面EFG∥平面BDD1B1.‎ - 9 -‎ ‎【证明】(1)连接SB,因为E,G分别是BC,SC的中点,所以EG∥SB.又因为SB平面BDD1B1,EG平面BDD1B1,所以直线EG∥平面BDD1B1.‎ ‎(2)连接SD,因为F,G分别是DC,SC的中点,所以FG∥SD.又因为SD平面BDD1B1,FG平面BDD1B1,所以FG∥平面BDD1B1,且EG平面EFG,FG平面EFG,EG∩FG=G,所以平面EFG∥平面BDD1B1.‎ ‎(15分钟　35分)‎ ‎1.(5分)下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是 (　　)‎ A.①③ B.①④ C.②③ D.②④‎ ‎【解析】选B.①中易知NP∥AA′,MN∥A′B,‎ 所以平面MNP∥平面AA′B,可得出AB∥平面MNP(如图).‎ ‎④中,NP∥AB,能得出AB∥平面MNP.‎ ‎2.(5分)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________________. ‎ ‎【解析】因为平面ABCD∥平面A1B1C1D1,‎ 所以MN∥PQ.因为M,N分别是A1B1,B1C1的中点,AP=,所以CQ=,从而DP=DQ=,所以PQ=a.‎ 答案:a - 9 -‎ ‎3.(5分)空间四边形ABCD的两条对棱AC,BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是________________. ‎ ‎【解析】设==k,所以==1-k,‎ 所以GH=5k,EH=4(1-k),所以周长=8+2k.‎ 又因为0