陕西省宝鸡中学2020届高三上学期第一次联考数学（理）试题 14页

五校联考 西安市第三中学 宝鸡中学 汉中市龙岗学校 ‎ 渭南高级中学 延安市新区高级中学 ‎2020届高三第一次五校联考理科数学试题（卷）‎ 命题：宝鸡中学 ‎ 校题：宝鸡中学 ‎ 本试卷分第I卷（选择题）和第II卷（非选择题）两部分 注意事项：‎ ‎1.答题前，考生先将自己的姓名、准考证号填写清楚，将条形码或二维码准确粘贴在条形码或二维码者粘贴处。‎ ‎2.答题时请按要求用笔。‎ ‎3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸、试卷上答题无效。‎ ‎4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。‎ ‎5.保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带或刮纸刀。‎ ‎ ‎ 第I卷 一．选择题（本题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）‎ 1. 已知集合，，则（ ）‎ ‎. . . .‎ 2. 设复数满足（是虚数单位），的共轭复数为，则（ ）‎ ‎. . . 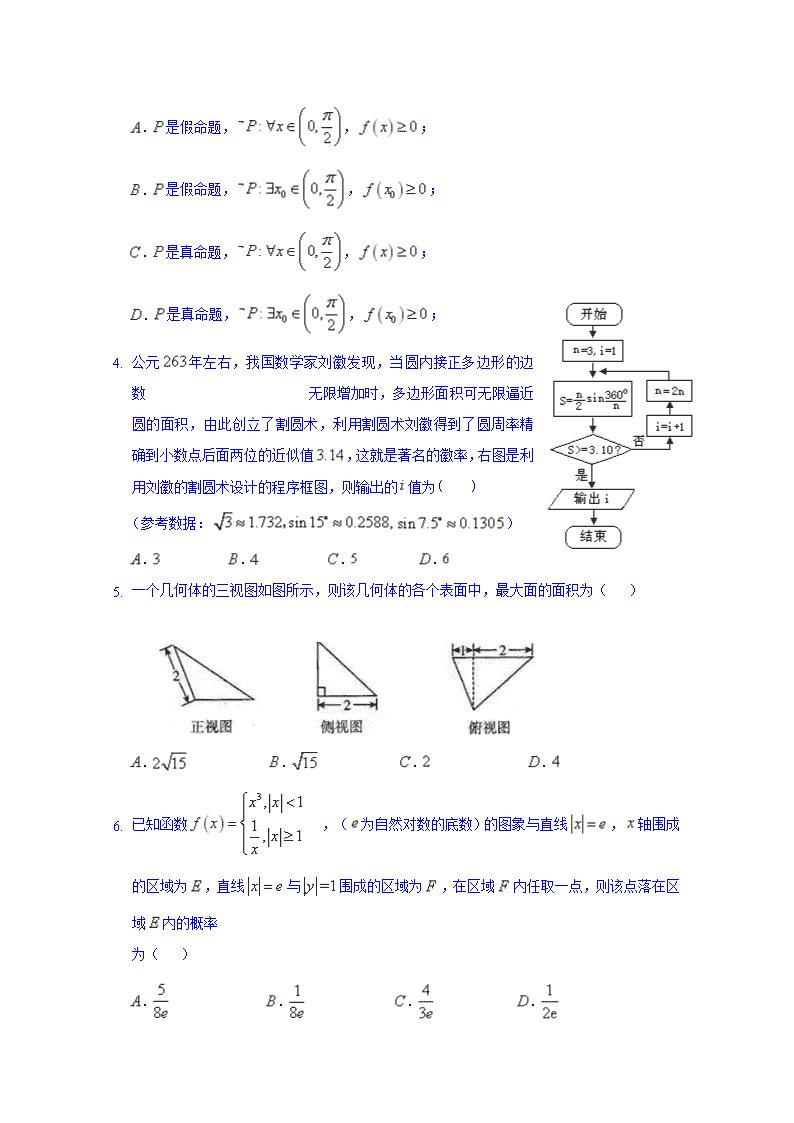.‎ 3. 已知，命题，，则（ ）‎ ‎.是假命题，，；‎ ‎.是假命题，，；‎ ‎.是真命题，，； ‎ ‎.是真命题，，；‎ 1. 公元年左右，我国数学家刘徽发现，当圆内接正多边形的边数 无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值，这就是著名的徽率，右图是利用刘徽的割圆术设计的程序框图，则输出的值为( )‎ ‎（参考数据：）‎ ‎. . . .‎ 2. 一个几何体的三视图如图所示，则该几何体的各个表面中，最大面的面积为（ ）‎ ‎. . . .‎ 3. 已知函数，（为自然对数的底数）的图象与直线，轴围成的区域为，直线与围成的区域为，在区域内任取一点，则该点落在区域内的概率 为（ ）‎ ‎. . . .‎ 1. 已知动点满足，且代数式的最小值为，则实数的取值为（ ）‎ ‎. . . .‎ 2. 已知函数（）的部分图象如图所示，点，是其上两点，若将的图象向右平移个单位长度，得到函数的图象，则函数图象的一条对称轴方程为（ ）‎ ‎. . . .‎ 3. 已知腰长为的等腰直角中，为斜边的中点，点为该平面内一动点，若，则的最小值为（ ）‎ ‎. . . .‎ 4. 已知、分别是具有公共焦点、的椭圆和双曲线的离心率，是两曲线的一个公共点，是的中点，且，则=（ ）‎ ‎. . . .‎ 5. 若数列的前项和满足：对都有（为常数）成立，则称数列为“和敛数列”，则数列，，， 中是“和敛数列”的有（ ）‎ ‎.个 .个 .个 .个 6. 定义在上的偶函数满足，且当时， ，若函数有三个零点，则正实数的取值范围为（ ‎ ‎ ）‎ ‎. . . . ‎ 第II卷 二．填空题：（本题共4小题，每小题5分，共20分）‎ 1. 已知函数，分别是定义在上的奇函数和偶函数，且，则_ _______________‎ 2. 设，若 ‎，则负实数______________‎ 3. 已知抛物线的焦点为，过点的直线与抛物线交于、两点，且直线与圆交于、两点，若，则直线的斜率为__________‎ 4. 在四面体中，，，，二面角的大小为，则四面体外接球的半径为________________‎ 三．解答题：（本题共70分. 解答应写出文字说明，证明过程或演算步骤）‎ 5. ‎（12分）已知在中，角，，的对边分别为，，，且 ⑴ 求角的大小；‎ ‎⑵若，求周长的最大值.‎ 6. ‎（12分）如图所示四边形与均为菱形，且 ⑴ 求证：平面；‎ ⑵ 求直线与平面所成角的正弦值.‎ 1. ‎（12分）2019年初，某市为了实现教育资源公平，办人民满意的教育，准备在今年8月份的小升初录取中在某重点中学实行分数和摇号相结合的录取办法。该市教育管理部门为了了解市民对该招生办法的赞同情况，随机采访了440名市民，将他们的意见和是否近三年家里有小升初学生的情况进行了统计，得到如下的列联表.‎ ‎ ‎ 赞同录取办法人数 不赞同录取办法人数 合计 近三年家里没有小升初学生 ‎180‎ ‎40‎ ‎220‎ 近三年家里有小升初学生 ‎140‎ ‎80‎ ‎220‎ 合计 ‎320‎ ‎120‎ ‎440‎ ‎(1)根据上面的列联表判断，能否在犯错误的概率不超过的前提下认为是否赞同小升初录取办法与近三年是否家里有小升初学生有关；‎ ‎(2)从上述调查的不赞同小升初录取办法人员中根据近三年家里是否有小升初学生按分层抽样抽出人，再从这人中随机抽出人进行电话回访，求人中恰有人近三年家里没有小升初学生的概率.‎ 附：，其中 2. ‎（12分）在平面直角坐标系中，点，分别为椭圆：的左右焦点，椭圆的离心率为，点在椭圆上，不在轴上的动点与动点关于原点对称，且四边形的周长为.‎ ‎⑴求动点的轨迹方程；‎ ‎⑵在动点的轨迹上有两个不同的点，，线段的中点为，已知点在圆上，求的最大值，并判断此时的形状.‎ 1. ‎（12分）已知函数（是常数，且）.‎ ‎(1)求函数的最值；‎ ‎⑵若函数在处取得极小值，且关于的方程在上恰有两个不相等的实数根，求实数的取值范围；‎ ⑴ 求证：当时，.‎ 2. ‎（分）选修：坐标系与参数方程 在平面直角坐标系中，直线的参数方程为（为参数）.在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为.‎ ⑴ 求直线的极坐标方程及曲线的直角坐标方程；‎ ‎⑵若是直线上的一点，是曲线上的一点，求的最大值.‎ 3. ‎（分）选修：不等式选讲 已知函数（）.‎ ⑴ 若，解不等式；‎ ‎⑵若不等式恒成立，求实数的取值范围.‎ ‎2020届高三第一次五校联考理科数学参考答案 一、选择题：(本大题共12小题，共60分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ A卷答案 D C C B B A C A C B C A B卷答案 B C D C B C A A D C B A 二、填空题：(本大题共4小题，共20分)‎ ‎13. ； 14. ； 15. ； 16. ‎ 三．解答题：(本大题共6小题，共70分)‎ ‎17.（12分）解: ⑴由题意得，所以，‎ 因为，所以，所以. .................................分 ‎⑵由已知及正、余弦定理得 整理得，所以. ....................................分 ‎ 所以由正弦定理得，‎ 所以，‎ 由得，所以，且 ...............分 所以 ‎，，‎ ‎，即 所以周长的最大值为. ...............分 ‎18.（12分）证明：⑴设与相交于点，连接，‎ 因为四边形为菱形，所以，且为的中点，‎ 因为，所以 又，所以平面 ...............分 ‎⑵连接，因为四边形为菱形，且，所以为等边三角形，‎ 因为为的中点，所以，又，，所以，， 两两垂直，建立如图所示的空间直角坐标系 ...............分 ‎ 设，因为四边形为菱形，，所以，‎ 因为为等边三角形，所以 所以，，，‎ 所以，，‎ 设平面的法向量为，则 令，得平面的一个法向量为， ...............................分 设直线与平面所成的角为，‎ 则.‎ 故直线与平面所成角的正弦值为. ...............................分 ‎19.（12分）解: ⑴假设是否赞同小升初录取办法与近三年是否有家里小升初学生无关，‎ 的观察值 因为 所以能在犯错误概率不超过的前提下认为是否赞同小升初录取办法与近三年是否家里有小升初学生有关. .........................分 ‎ ‎⑵设从近三年家里没有小升初学生的人员中抽出人，从近三年家里有小升初学生的人员中抽出人，‎ 由分层抽样的定义可知，解得，. ....................分 方法一：设事件为人中恰有人近三年家里没有小升初学生，在抽出的人中，近三年家里没有小升初学生的人，分别记为，，近三年家里有小升初学生的人，分别记为，，，，则从这人中随机抽出人有种不同的抽法，所有的情况如下：‎ ‎， ， ， ，，，‎ ‎，，，，，，，，，，，，，. ....................分 其中恰有人近三年家里没有小升初学生的情况有种，分别为：‎ ‎，，，，，，，， ，，， ‎ 所以人中恰有人近三年家里没有小升初学生的概率为. ..........分 ‎ 方法二：设事件为人中恰有人近三年家里没有小升初学生，在抽出的 人中，近三年家里没有小升初学生的有人，近三年家里有小升初学生的有人，则从这人中随机抽出人有种不同的抽法，从这人中随机抽出的人中恰有人近三年家里没有小升初学生的情况共有种. ...............分 所以人中恰有人近三年家里没有小升初学生的概率为:‎ ‎ ...........................分 ‎20.（12分）解: ⑴设点，的坐标分别为，‎ 由已知可知，又，所以可得，‎ 则， ...............分 连接，因为，，所以四边形为平行四边形.‎ 因为四边形的周长为，所以， .............分 所以动点的轨迹是以点，分别为左、右焦点，长轴长为的椭圆（除去左、右顶点），可得动点的轨迹方程为 ‎⑵因为，，，所以 所以 ‎ ............分 当且仅当，即时，等号成立，‎ 所以的最大值为 ...............分 ‎21.（12分）解: ⑴由已知可知函数的定义域为；‎ 由，得；由，得，所以函数在区间上单调递增，在区间上单调递减 故当时函数取得最小值为，没有最大值. ........................分 ‎ ‎⑵由题意，得，，即， ........................分 ‎，由，‎ 得，即，‎ 设，‎ 则，‎ 当时，，的变化情况如下表：‎ ‎+‎ 方程在上恰有两个不相等的实数根，‎ ‎，，，即 ........分 ‎⑶证明：由⑴和⑵可知当时，即，‎ 当时， ........................分 令，则， 当，时，‎ 即 ‎ ........................分 ‎22.（10分）解:⑴直线的参数方程为（为参数），‎ 消去参数，得直线的普通方程为；‎ 由，得直线的极坐标方程为，‎ 即 ........................分 曲线的极坐标方程为，即，‎ 由，，得曲线的直角坐标方程为. .........分 ‎⑵在直线上，在曲线上，‎ ‎，， ........................分 当时，的最大值为 ........................分 ‎23.（10分）解: ⑴解法一：，不等式可化为，‎ 或或 ........................分 或或 或或 ........................分 ‎，即不等式的解集为 ........................分 解法二：，则 ........................分 在同一平面直角坐标系中画出函数和的图象，如图所示 ........................分 由图可知，不等式的解集为 ..........分 ‎⑵由于 ‎ ‎ ..........................分 所以当时，最小，即， ..........................分 所以要使恒成立，只需即可，‎ 所以，即实数的取值范围为 ..........................分