【数学】2020届一轮复习（文）通用版5-1平面向量的概念及线性运算学案 13页

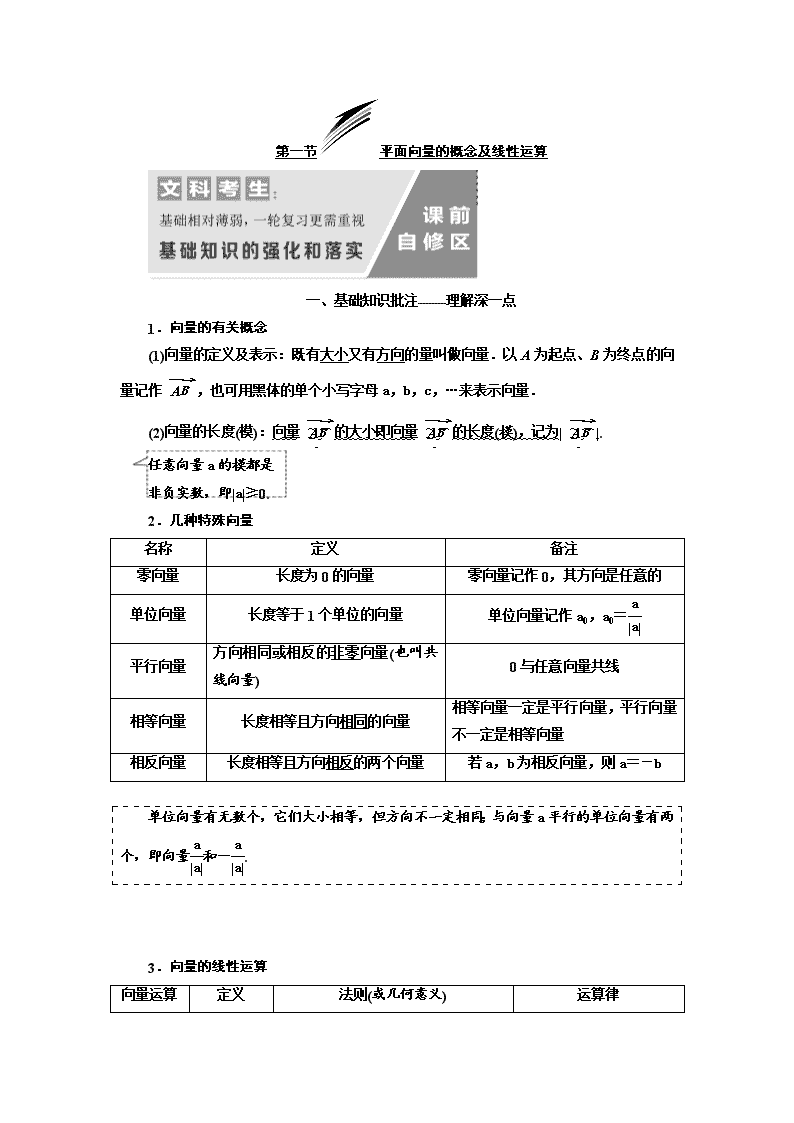
第一节平面向量的概念及线性运算 一、基础知识批注——理解深一点 ‎1．向量的有关概念 ‎(1)向量的定义及表示：既有大小又有方向的量叫做向量．以A为起点、B为终点的向量记作，也可用黑体的单个小写字母a，b，c，…来表示向量．‎ ‎(2)向量的长度(模)：向量的大小即向量的长度(模)，记为||.　　　　　　　　　　　　　　　　 　　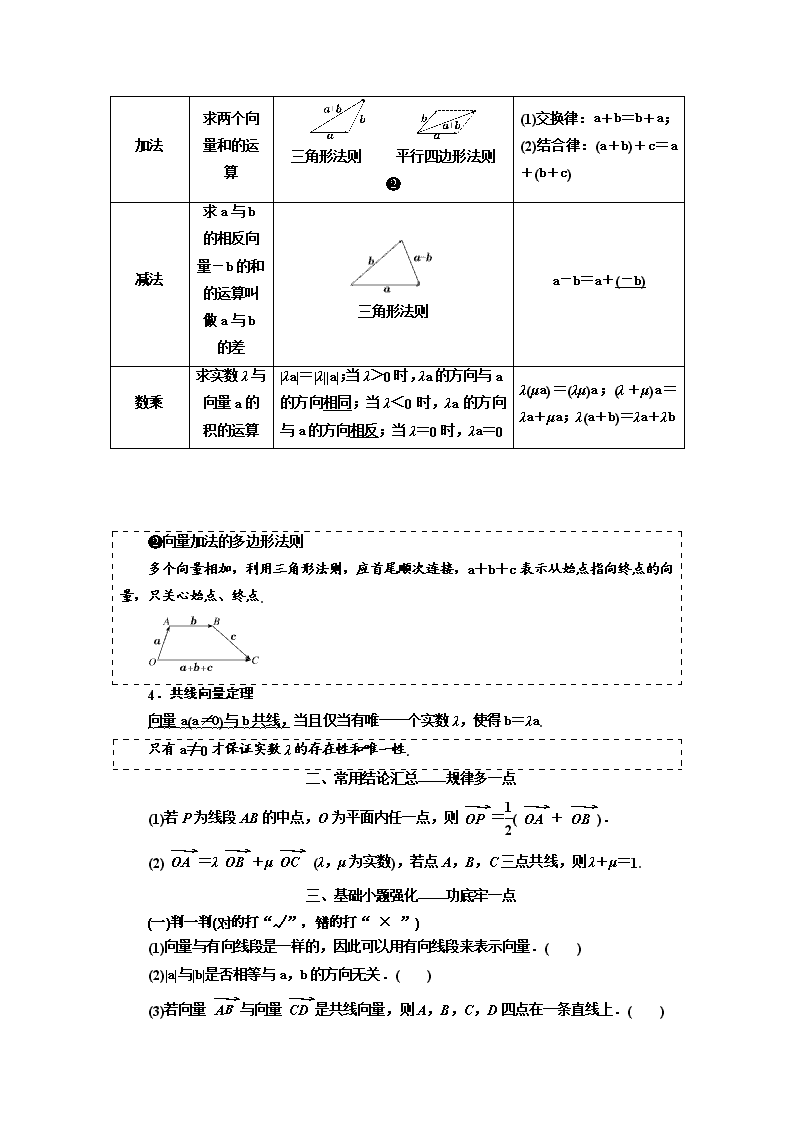‎ 任意向量a的模都是 非负实数，即|a|≥0.‎ ‎2．几种特殊向量 名称 定义 备注 零向量 长度为0的向量 零向量记作0，其方向是任意的 单位向量 长度等于1个单位的向量　‎ 单位向量记作a0，a0＝ 平行向量 方向相同或相反的非零向量(也叫共线向量)‎ ‎0与任意向量共线 相等向量 长度相等且方向相同的向量 相等向量一定是平行向量，平行向量不一定是相等向量 相反向量 长度相等且方向相反的两个向量 若a，b为相反向量，则a＝－b 单位向量有无数个，它们大小相等，但方向不一定相同；与向量a平行的单位向量有两个，即向量和－.‎ ‎3．向量的线性运算 向量运算 定义 法则(或几何意义)‎ 运算律 加法 求两个向量和的运算　‎ ‎ ‎ 三角形法则 平行四边形法则 ‎❷‎ ‎(1)交换律：a＋b＝b＋a；‎ ‎(2)结合律：(a＋b)＋c＝a＋(b＋c)‎ 减法 求a与b的相反向量－b的和的运算叫做a与b的差 三角形法则 a－b＝a＋(－b)‎ 数乘 求实数λ与向量a的积的运算 ‎|λa|＝|λ||a|；当λ＞0时，λa的方向与a的方向相同；当λ＜0时，λa的方向与a的方向相反；当λ＝0时，λa＝0‎ λ(μa)＝(λμ)a；(λ＋μ)a＝λa＋μa；λ(a＋b)＝λa＋λb ‎❷向量加法的多边形法则 多个向量相加，利用三角形法则，应首尾顺次连接，a＋b＋c表示从始点指向终点的向量，只关心始点、终点.‎ ‎4．共线向量定理 向量a(a≠0)与b共线，当且仅当有唯一一个实数λ，使得b＝λa.‎ 只有a≠0才保证实数λ的存在性和唯一性.‎ 二、常用结论汇总——规律多一点 ‎(1)若P为线段AB的中点，O为平面内任一点，则＝(＋)．‎ ‎(2)＝λ＋μ (λ，μ为实数)，若点A，B，C三点共线，则λ＋μ＝1.‎ 三、基础小题强化——功底牢一点 ‎(1)向量与有向线段是一样的，因此可以用有向线段来表示向量．(　　)‎ ‎(2)|a|与|b|是否相等与a，b的方向无关．(　　)‎ ‎(3)若向量与向量是共线向量，则A，B，C，D四点在一条直线上．(　　)‎ ‎(4)当两个非零向量a，b共线时，一定有b＝λa，反之成立．(　　)‎ 答案：(1)×　(2)√　(3)×　(4)√‎ ‎(二)选一选 ‎1．下列说法正确的是(　　)‎ A．单位向量都相等 B．模为0的向量与任意向量共线 C．平行向量不一定是共线向量 D．任一向量与它的相反向量不相等 解析：选B　对于A，单位向量的模相等，方向不一定相同，所以A错误；对于B，模为0的向量为零向量，零向量和任意向量共线，所以B正确；对于C，共线向量是方向相同或相反的非零向量，也叫平行向量，所以C错误；对于D，零向量与它的相反向量相等，所以D错误．故选B.‎ ‎2．在平行四边形ABCD中，下列结论错误的是(　　)‎ A．||＝||一定成立 　B．＝＋一定成立 C．＝一定成立 D．＝－一定成立 解析：选A　在平行四边形ABCD中，＝＋一定成立，＝一定成立，＝－一定成立，但||＝||不一定成立．故选A.‎ ‎3．设a，b都是非零向量，下列四个选项中，一定能使＋＝0成立的是(　　)‎ A．a＝2b B．a∥b C．a＝－b D．a⊥b 解析：选C　“＋＝0，且a，b都是非零向量”等价于“非零向量a，b共线且反向”，故答案为C.‎ ‎(三)填一填 ‎4．若菱形ABCD的边长为2，则|－＋|＝________.‎ 解析：|－＋|＝|＋＋|＝||＝2.‎ 答案：2‎ ‎5．已知a与b是两个不共线向量，且向量a＋λb与－(b－3a)共线，则λ＝________.‎ 解析：由题意知存在k∈R，使得a＋λb＝k[－(b－3a)]，‎ 所以解得 答案：－ ‎ ‎[典例]　给出下列命题：‎ ‎①若a＝b，b＝c，则a＝c；‎ ‎②若A，B，C，D是不共线的四点，则＝是四边形ABCD为平行四边形的充要条件；‎ ‎③a＝b的充要条件是|a|＝|b|且a∥b；‎ ‎④若a∥b，b∥c，则a∥c.‎ 其中正确命题的序号是________．‎ ‎[解析]　①正确．∵a＝b，∴a，b的长度相等且方向相同，‎ 又b＝c，∴b，c的长度相等且方向相同，‎ ‎∴a，c的长度相等且方向相同，故a＝c.‎ ‎②正确．∵＝，∴||＝||且∥，‎ 又A，B，C，D是不共线的四点，‎ ‎∴四边形ABCD为平行四边形；‎ 反之，若四边形ABCD为平行四边形，‎ 则∥且||＝||，因此，＝.‎ ‎③不正确．当a∥b且方向相反时，即使|a|＝|b|，也不能得到a＝b，故|a|＝|b|且a∥b不是a＝b的充要条件，而是必要不充分条件．‎ ‎④不正确．考虑b＝0这种特殊情况．‎ 综上所述，正确命题的序号是①②.‎ ‎[答案]　①②‎ ‎[解题技法]　向量有关概念的关键点 ‎(1)向量定义的关键是方向和长度．‎ ‎(2)非零共线向量的关键是方向相同或相反，长度没有限制．‎ ‎(3)相等向量的关键是方向相同且长度相等．‎ ‎(4)单位向量的关键是长度都是一个单位长度．‎ ‎(5)零向量的关键是长度是0，规定零向量与任意向量共线．‎ ‎[题组训练]‎ ‎1．给出下列命题：‎ ‎①两个具有公共终点的向量，一定是共线向量；‎ ‎②λa＝0(λ为实数)，则λ必为零；‎ ‎③λ，μ为实数，若λa＝μb，则a与b共线．‎ 其中错误的命题的个数为(　　)‎ A．0　　　　　　　　　　 　B．1‎ C．2 D．3‎ 解析：选D　①错误，两向量共线要看其方向而不是起点或终点．②错误，当a＝0时，不论λ为何值，λa＝0.③错误，当λ＝μ＝0时，λa＝μb＝0，此时，a与b可以是任意向量．故错误的命题有3个，故选D.‎ ‎2．设a0为单位向量，下列命题中：①若a为平面内的某个向量，则a＝|a|·a0；②若a与a0平行，则a＝|a|a0；③若a与a0平行且|a|＝1，则a＝a0，假命题的个数是(　　)‎ A．0 B．1‎ C．2 D．3‎ 解析：选D　向量是既有大小又有方向的量，a与|a|a0的模相同，但方向不一定相同，故①是假命题；若a与a0平行，则a与a0的方向有两种情况：一是同向，二是反向，反向时a＝－|a|a0，故②③也是假命题．‎ 综上所述，假命题的个数是3.‎ ‎ ‎[典例]　(1)(2018·全国卷Ⅰ)在△ABC中，AD为BC边上的中线，E为AD的中点，则＝(　　)‎ A.－ B.－ C.＋ D.＋ ‎(2)如图，在直角梯形ABCD中，＝，＝2， 且＝r＋s，则2r＋3s＝(　　)‎ A．1 B．2‎ C．3 D．4‎ ‎[解析]　(1)作出示意图如图所示．＝＋＝＋＝ ×(＋)＋(－)＝－.故选A.‎ ‎(2)根据图形，由题意可得＝＋＝＋＝＋(＋＋)＝＋(＋)＝＋＝＋.‎ 因为＝r＋s，所以r＝，s＝，则2r＋3s＝1＋2＝3.‎ ‎[答案]　(1)A　(2)C ‎[解题技法]　向量线性运算的解题策略 ‎(1)常用的法则是平行四边形法则和三角形法则，一般共起点的向量求和用平行四边形法则，求差用三角形法则，求首尾相连的向量的和用三角形法则．‎ ‎(2)找出图形中的相等向量、共线向量，将所求向量与已知向量转化到同一个平行四边形或三角形中求解．‎ ‎(3)用几个基本向量表示某个向量问题的基本技巧：‎ ‎①观察各向量的位置；②寻找相应的三角形或多边形；③运用法则找关系；④化简结果．‎ ‎(4)与向量的线性运算有关的参数问题，一般是构造三角形，利用向量运算的三角形法则进行加法或减法运算，然后通过建立方程组即可求得相关参数的值．‎ ‎[题组训练]‎ ‎1．设D为△ABC所在平面内一点，＝3，则(　　)‎ A．＝－＋　　 　B．＝－ C．＝＋ D．＝－ 解析：选A　由题意得＝＋＝＋＝＋－＝－＋.‎ ‎2．(2019·太原模拟)在正方形ABCD中，M，N分别是BC，CD的中点，若＝λ＋μ，则实数λ＋μ＝________.‎ 解析：如图，∵＝＋＝＋＝＋，①‎ ＝＋＝＋，②‎ 由①②得＝－，＝－，‎ ‎∴＝＋＝＋＝－＋－＝＋，‎ ‎∵＝λ＋μ，∴λ＝，μ＝，λ＋μ＝.‎ 答案： ‎ ‎[典例]　设两个非零向量a与b不共线，‎ ‎(1)若＝a＋b，＝2a＋8b，＝3a－3b，‎ 求证：A，B，D三点共线；‎ ‎(2)试确定实数k，使ka＋b和a＋kb同向．‎ ‎[解]　(1)证明：∵＝a＋b，＝2a＋8b，＝3a－3b，‎ ‎∴＝＋＝2a＋8b＋3a－3b＝5(a＋b)＝5，‎ ‎∴，共线．‎ 又∵它们有公共点B，‎ ‎∴A，B，D三点共线．‎ ‎(2)∵ka＋b与a＋kb同向，‎ ‎∴存在实数λ(λ>0)，使ka＋b＝λ(a＋kb)，‎ 即ka＋b＝λa＋λkb.‎ ‎∴(k－λ)a＝(λk－1)b.‎ ‎∵a，b是不共线的非零向量，‎ ‎∴解得或 又∵λ>0，∴k＝1.‎ ‎[解题技法]‎ ‎1．共线向量定理的3个应用 证明向量共线 对于向量a，b，若存在实数λ，使a＝λb(b≠0)，则a与b共线 证明三点共线 若存在实数λ，使＝λ，则A，B，C三点共线 求参数的值 利用共线向量定理及向量相等的条件列方程(组)求参数的值 ‎2.向量共线问题的注意事项 ‎(1)向量共线的充要条件中，当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，注意待定系数法和方程思想的运用．‎ ‎(2)证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得到三点共线．‎ ‎[题组训练]‎ ‎1．在四边形ABCD中，＝a＋2b，＝－4a－b，＝－5a－3b，则四边形ABCD的形状是(　　)‎ A．矩形　　　　　　　　 　B．平行四边形 C．梯形 D．以上都不对 解析：选C　由已知，得＝＋＋＝－8a－2b＝2(－4a－b)＝2，故∥.又因为与不平行，所以四边形ABCD是梯形．‎ ‎2．已知向量e1≠0，λ∈R，a＝e1＋λe2，b＝2e1，若向量a与向量b共线，则(　　)‎ A．λ＝0 B．e2＝0‎ C．e1∥e2 D．e1∥e2或λ＝0‎ 解析：选D　因为向量e1≠0，λ∈R，a＝e1＋λe2，b＝2e1，又因为向量a和b共线，存在实数k，使得a＝kb，所以e1＋λe2＝2ke1，所以λe2＝(2k－1)e1，所以e1∥e2或λ＝0.‎ ‎3．已知O为△ABC内一点，且＝(＋)，＝t，若B，O，D三点共线，则t＝(　　)‎ A. B. C. D. 解析：选B　设E是BC边的中点，则(＋)＝，由题意得＝，所以＝＝(＋)＝＋，又因为B，O，D三点共线，所以＋＝1，解得t＝，故选B.‎ ‎4．已知O，A，B三点不共线，P为该平面内一点，且＝＋，则(　　)‎ A．点P在线段AB上 B．点P在线段AB的延长线上 C．点P在线段AB的反向延长线上 D．点P在射线AB上 解析：选D　由＝＋，得－＝，∴＝·，∴点P在射线AB上，故选D.‎ ‎1．设D，E，F分别为△ABC的三边BC，CA，AB的中点，则＋＝(　　)‎ A． 　　　　　　　　　　 　B. C. D． 解析：选A　由题意得＋＝(＋)＋(＋)＝(＋)＝.‎ ‎2．已知向量a，b不共线，且c＝λa＋b，d＝a＋(2λ－1)b，若c与d共线反向，则实数λ的值为(　　)‎ A．1 B．－ C．1或－ D．－1或－ 解析：选B　由于c与d共线反向，则存在实数k使c＝kd(k＜0)，‎ 于是λa＋b＝k.‎ 整理得λa＋b＝ka＋(2λk－k)b.‎ 由于a，b不共线，所以有 整理得2λ2－λ－1＝0，解得λ＝1或λ＝－.‎ 又因为k＜0，所以λ＜0，故λ＝－.‎ ‎3．设向量a，b不共线，＝2a＋pb，＝a＋b，＝a－2b，若A，B，D三点共线，则实数p的值为(　　)‎ A．－2 B．－1‎ C．1 D．2‎ 解析：选B　因为＝a＋b，＝a－2b，所以＝＋＝2a－b.又因为A，B，D三点共线，所以，共线．设＝λ，所以2a＋pb＝λ(2a－b)，所以2＝2λ，p＝－λ，即λ＝1，p＝－1.‎ ‎4．(2019·甘肃诊断)设D为△ABC所在平面内一点，＝－4，则＝(　　)‎ A.－ B.＋ C.－ D.＋ 解析：选B　法一：设＝x＋y，由＝－4可得，＋＝－4－4，即－－3＝－4x－4y，则解得即＝＋，故选B.‎ 法二：在△ABC中，＝－4，即－＝，则＝＋＝－＝－(＋)＝＋，故选B.‎ ‎5．在平面直角坐标系中，O为坐标原点，A，B，C三点满足＝＋，则等于(　　)‎ A．1 B．2‎ C．3 D. 解析：选C　因为＝－＝＋－＝，＝－＝＋－＝，所以＝3.故选C.‎ ‎6．已知△ABC的边BC的中点为D，点G满足＋＋＝0，且＝λ，则λ的值是(　　)‎ A. B．2‎ C．－2 D．－ 解析：选C　由＋＋＝0，得G为以AB，AC为邻边的平行四边形的第四个顶点，因此＝－2，则λ＝－2.故选C.‎ ‎7．下列四个结论：‎ ‎①＋＋＝0；②＋＋＋＝0；‎ ‎③－＋－＝0；④＋＋－＝0，‎ 其中一定正确的结论个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析：选C　①＋＋＝＋＝0，①正确；②＋＋＋＝＋＋＝，②错误；③－＋－＝＋＋＝＋＝0，③正确；④＋＋－＝＋＝0，④正确．故①③④正确．‎ ‎8.如图，在平行四边形ABCD中，M，N分别为AB，AD上的点，且＝，＝，AC，MN交于点P.若＝λ，则λ的值为(　　)‎ A. B. C. D. 解析：选D　∵＝，＝，∴＝λ＝λ(＋)＝λ＝λ＋λ.∵点M，N，P三点共线，∴λ＋λ＝1，则λ＝.故选D.‎ ‎9．设向量a，b不平行，向量λa＋b与a＋2b平行，则实数λ＝________.‎ 解析：因为向量λa＋b与a＋2b平行，‎ 所以可设λa＋b＝k(a＋2b)，则所以λ＝.‎ 答案： ‎10．若＝，＝(λ＋1)，则λ＝________.‎ 解析：如图，由＝，可知点P是线段AB上靠近点A的三等分点，‎ 则＝－，结合题意可得λ＋1＝－，所以λ＝－.‎ 答案：－ ‎11．已知平行四边形ABCD的对角线AC和BD相交于O，且＝a，＝b，则＝________，＝________.(用a，b表示)‎ 解析：如图，＝＝－＝b－a，＝－＝－－＝－a－b.‎ 答案：b－a　－a－b ‎12．(2019·长沙模拟)在平行四边形ABCD中，M为BC的中点．若＝λ＋μ，则λ－μ＝________.‎ 解析：如图，在平行四边形ABCD中，＝，所以＝＋＝＋＝＋(－)＝＋(－)＝＋－，所以＝＋，所以＝＋，所以λ＝，μ＝，所以λ－μ＝.‎ 答案： ‎13．设e1，e2是两个不共线的向量，已知＝2e1－8e2，＝e1＋3e2，＝2e1－e2.‎ ‎(1)求证：A，B，D三点共线；‎ ‎(2)若＝3e1－ke2，且B，D，F三点共线，求k的值．‎ 解：(1)证明：由已知得＝－＝(2e1－e2)－(e1＋3e2)＝e1－4e2，‎ ‎∵＝2e1－8e2，‎ ‎∴＝2.‎ 又∵与有公共点B，‎ ‎∴A，B，D三点共线．‎ ‎(2)由(1)可知＝e1－4e2，‎ ‎∵＝3e1－ke2，且B，D，F三点共线，‎ ‎∴存在实数λ，使＝λ，‎ 即3e1－ke2＝λe1－4λe2，‎ 得 解得k＝12.‎