高二数学选修4-4~4_1_2(1)极坐标系_ 30页

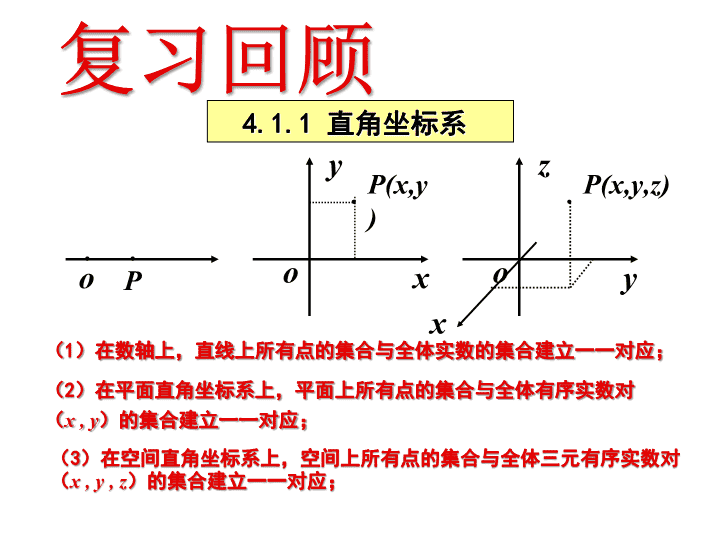
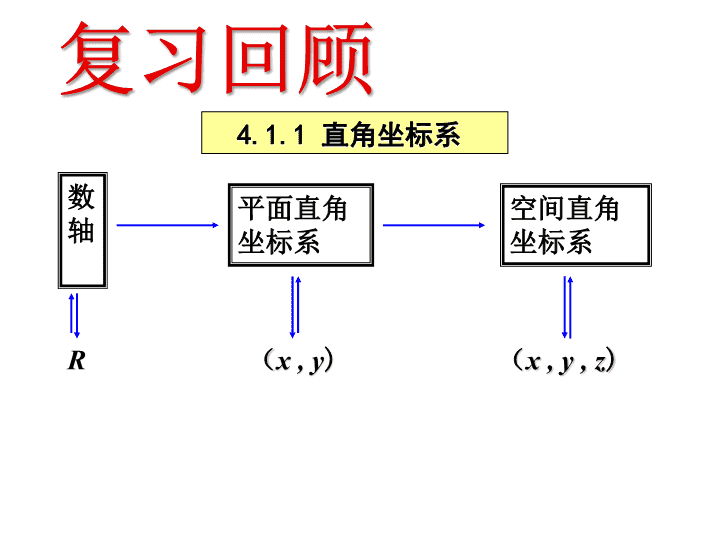
4.1.2(1) 极坐标系 高中数学选修 4-4 坐标系与参数方程 学习要点： 极坐标系是不同于直角坐标系的另一种坐标系，在这两种坐标系中都可以确定点的位置，其各有特点。通常情况下，在运动的过程中，若点作平移变动，则选择直角坐标系；而若点作旋转变动，则采用极坐标系。 x y o y z o x ● ● ● ● o P P(x,y) P(x,y,z) （ 1 ）在数轴上，直线上所有点的集合与全体实数的集合建立一一对应； （ 2 ）在平面直角坐标系上，平面上所有点的集合与全体有序实数对 （ x , y ）的集合建立一一对应； （ 3 ）在空间直角坐标系上，空间上所有点的集合与全体三元有序实数对（ x , y , z ）的集合建立一一对应； 复习回顾 4.1.1 直角坐标系 4.1.1 直角坐标系 数 轴 空间直角坐标系 平面直角坐标系 R （ x , y ) （ x , y , z ) 复习回顾 建系时，根据几何特点选择适当的直角坐标系 : （ 1 ）若图形有对称中心，则可选对称中心为坐标原点； （ 2 ）若图形有对称轴，则可选择对称轴为坐标轴； （ 3 ）建系应使图形上的特殊点尽可能多的在坐标轴上。 建立坐标系是为了确定点的位置。由此，在所创建的坐标系中，应满足： 任意一点都存在一个坐标与之对应；反之，依据一个点的坐标就能确定这个点的位置； 而确定点的位置即为求出此点在设定的坐标系中的坐标。 复习回顾 选择适当的坐标系，表示边长为 1 的正六边形的顶点。 巩固练习 O y x F A E B D C （ 1 ） 若有一艘军舰巡逻在海面上，发现前方有一群水雷，如何确定他们的位置以便将它们引爆呢？ 军 舰 水雷群 创设情境 创设情境 从这向北 1000 米 请问去 农行路 怎么走？ 请分析上面这句话，他告诉了问路人什么？ 从这向北走 1000 米！ 出发点 方向 距 离 在生活中人们经常用方向和距离来表示一点的位置。这种用 方向 和 距离 表示平面上一点的位置的思想，就是 极坐标 的基本思想。 情境分析 一、极坐标系的建立： 在平面内取一个定点 O ，叫做 极点 。 引一条射线 O x ，叫做 极轴 。 再选定一个长度单位和 角度单位 及 它的正方向 （通常取逆时针方向）。 这样就建立了一个 极坐标系 。 x O 新课讲解 二、极坐标系内一点的极坐标的规定 : 对于平面上任意一点 M ，用  表示线段 OM 的长度，用  表示从 O x 到 OM 的角度，  叫做点 M 的 极径 ，  叫做点 M 的 极角 ，有序数对 （ ，） 就叫做 M 的极坐标。 特别强调： 表示线段 OM 的长度，即点 M 到极点 O 的距离；表示从 O x 到 OM 的角度，即以 O x （极轴）为始边， OM 为终边的角。 x O M   新课讲解 题组 1 ：说出下图中各点的极坐标 练一练 ①平面上一点的极坐标是否唯一？ ②若不唯一，那有多少种表示方法？ ③坐标不唯一是由谁引起的？ ④不同的极坐标是否可以写出统一表达式？ 特别规定 : 当 M 在极点时，它的极坐标  =0 ，可以取任意值。 想一想？ 三、点的极坐标的表达式的研究 : X O M   如图： OM 的长度为 4 ， 请说出点 M 的极坐标的其他表达式 . 思考：这些极坐标之间有何异同？ 思考：这些极角有何关系？ 这些极角的始边相同，终边也相同。也就是说它们是终边相同的角。 本题点 M 的极坐标统一表达式： 极径相同，不同的是极角。 新课讲解 题组 2 ：在极坐标系里描出下列各点 练一练 A B C D E F G O X 解析： 四、 1 、负极径的定义 说明：一般情况下，极径都是正值；在某些必要情况下，极径也可以取负值。 对于点 M （ ，） 负极径时的规定： [1] 作射线 OP ，使  XOP=  [2] 在 OP 的反向延长 线上取一点 M ，使  OM=   ; 如图示： O X P  M 新课讲解 O X P  = /4 M 2 、负极径的实例 在极坐标系中画出点 :M （－ 3 ，  /4 ） 的位置 [1] 作射线 OP ，使  XOP= /4 [2] 在 OP 的反向延长线上取一点 M ，使  OM= 3; 如图示： M （－ 3 ，  /4 ） 新课讲解 ● 题组 3 ：说出下图中当极径取负值时各点的极坐标 练一练 3 、关于负极径的思考 “负极径”真是“负”的吗？ 根据极径定义，极径是距离，当然是正的。现在所说的“负极径”中的“负”到底是什么意思？ 思考： 试把负极径时点的确定过程，与正极径时点的确定过程相比较，看看有什么相同，有什么不同？ ？？？ 新课讲解 4 、正、负极径时，点的确定过程比较 O X P O X P [1] 作射线 OP ，使  XOP= /4 [2] 在 OP 的反向延长线上取一点 M ，使  OM= 3 [1] 作射线 OP ，使  XOP= /4 [2] 在 OP 的上取一点 M ，使  OM= 3 M 画出点 : （ 3 ，  /4 ） 和（－ 3 ，  /4 ） 给定 ρ ,θ 在极坐标系中描点的方法： 先按极角 找到 极径所在的射线 ，后 按极径的正负和数值 在这条射线或其反向延长线上描点。 M 5 、负极径的实质 从比较来看，负极径比正极径多了一个操作，将射线 OP“ 反向延长 ”。 O X P M O X P M 而反向延长也可以看成是旋转  ， 因此，所谓“负极径”实质是 针对方向 的。这与数学中通常的习惯一致，用“负”表示“反向 ”。 负极径小结： 极径变为负 ， 极角增加  。 练习：写出点 的负极径的极坐标 （ 6 ， ） 答：（－ 6 ， +π ） 或（－ 6 ，－ +π ） 特别强调： 一般情况下（若不作特别说明时），认为  ≥ 0 。因为负极径只在极少数情况使用。 五、极坐标系下点的极坐标 O X P M 探索点 M （ 3 ，  /4 ）的所有极坐标 [1] 极径是正的时候： [2] 极径是负的时候： 六、极坐标系下点与它的极坐标的对应情况 [1] 给定（  , ） , 就可以在 极坐标 平面内确定唯一的一点 M 。 [2] 给定平面上一点 M ，但却有无数个极坐标与之对应。 原因在于：极角有无数个。 O X P M (ρ,θ)… 新课讲解 一般地 , 若 ( ρ ,θ ) 是一点 M 的极坐标 , 则 ( ρ ,θ +2 k π ) 或 ( － ρ,θ+(2 k + 1)π ) 都可以作为它的极坐标 . 若 限定 ρ ＞ 0,0≤θ ＜ 2π 或－ π ＜ θ≤ π , 则 除极点 外 , 平面内的点和极坐标就可 一一对应 了 . 六、极坐标系下点与它的极坐标的对应情况 2. 在极坐标系中 , 与 (ρ,θ) 关于极轴对称的点是 ( ) A.( － ρ,θ) B.( － ρ, － θ) C.( － ρ,θ ＋ π) D.( － ρ,π － θ) C D 题组 4 1. 在极坐标系中，与点 ( － 3, ) 重合的点是 ( ) A.(3, ) B. ( － 3, － ) C. (3, － ) D. ( － 3, － ) 3. 在极坐标系中 , 与点 ( － 8, ) 关于极点对称的点 的一个坐标是 ( ) A.(8, ) B. (8, － ) C. ( － 8, ) D.( － 8, － ) A [3] 一点的极坐标 是 否 有 统一的表达式？ [1] 建立一个极坐标系需要哪些要素？ 极点；极轴；长度单位；角度单位和它的正方向。 [2] 极坐标系内一点的极坐标有多少种表达式？ 无数 . 极径有正有负； 极角也有正负且无数个。 有 . （ ρ ， 2 k π+θ ） 课堂小结 或 （ - ρ ， 2 k π+θ + π ） 课堂小结 1 、极坐标 （ ρ ， 2 k π+θ ） 和 （ - ρ ， 2 k π+θ + π ） 其中 表示同一个点 （ ρ ， θ ） ； 2 、点 M （ ρ ， θ ） 关于极点的对称点的一个坐标为 （ - ρ ， θ ） 或 （ ρ ， π+θ ） ； 3 、点 M （ ρ ， θ ） 关于极轴的对称点的一个坐标为 （ ρ ， - θ ） 或 （ - ρ ， π - θ ） ； 4 、点 M （ ρ ， θ ） 关于直线 的对称点的一个坐标为 （ - ρ ， - θ ） 或 （ ρ ， π - θ ） ； 课外作业