2018届二轮复习直线与圆锥曲线的位置关系学案 4页

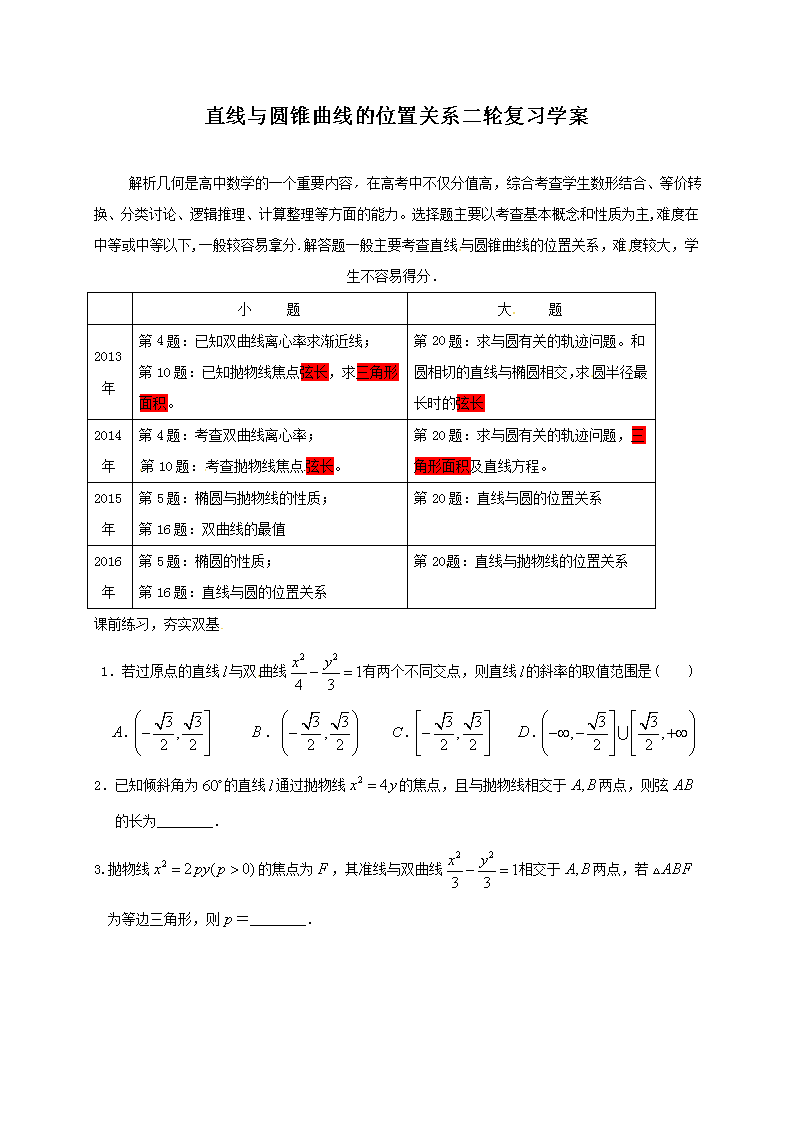
直线与圆锥曲线的位置关系二轮复习学案 ‎ ‎ ‎ 解析几何是高中数学的一个重要内容，在高考中不仅分值高，综合考查学生数形结合、等价转换、分类讨论、逻辑推理、计算整理等方面的能力。选择题主要以考查基本概念和性质为主,难度在中等或中等以下,一般较容易拿分.解答题一般主要考查直线与圆锥曲线的位置关系，难度较大，学生不容易得分．‎ 小 题 大 题 ‎2013年 第4题：已知双曲线离心率求渐近线；‎ 第10题：已知抛物线焦点弦长，求三角形面积。‎ 第20题：求与圆有关的轨迹问题。和圆相切的直线与椭圆相交，求圆半径最长时的弦长 ‎2014年 第4题：考查双曲线离心率；‎ 第10题：考查抛物线焦点弦长。‎ 第20题：求与圆有关的轨迹问题，三角形面积及直线方程。‎ ‎2015年 第5题：椭圆与抛物线的性质；‎ 第16题：双曲线的最值 第20题：直线与圆的位置关系 ‎2016年 第5题：椭圆的性质；‎ 第16题：直线与圆的位置关系 第20题：直线与抛物线的位置关系 课前练习，夯实双基 ‎ 1．若过原点的直线与双曲线有两个不同交点，则直线的斜率的取值范围是(　　)‎ ‎. ． . .‎ ‎2．已知倾斜角为的直线通过抛物线的焦点，且与抛物线相交于两点，则弦的长为________．‎ ‎3.抛物线的焦点为，其准线与双曲线相交于两点，若为等边三角形，则＝________．‎ 题型一：弦长问题 例、（年新课标 文数 第题）在直角坐标系中，直线交轴于点，交抛物线C：于点，关于点的对称点为，连结并延长交于点.‎ ‎（I）求；（II）除以外，直线与是否有其它公共点？说明理由.[来源:学§科§网]‎ ‎[来源:Zxxk.Com]‎ 题型二：面积问题 例、已知椭圆的中心在坐标原点，长轴长为，离心率，过右焦点的直线交椭圆于，两点.‎ ‎（I）求椭圆的方程； （II）当直线的斜率为时，求的面积；‎ ‎【变式训练】题目条件不变，将结论改为“求面积的最大值”．‎ ‎[来源:Z.xx.k.Com]‎ 题型三：定点定值问题（备用）：‎ 例、已知椭圆：，若直线与椭圆相交于，两点（不是左右顶点），且以为直径的圆过椭圆的右顶点，求证：直线过定点，并求出该定点的坐标． ‎