高中数学选修2-2课件3_2_1 44页

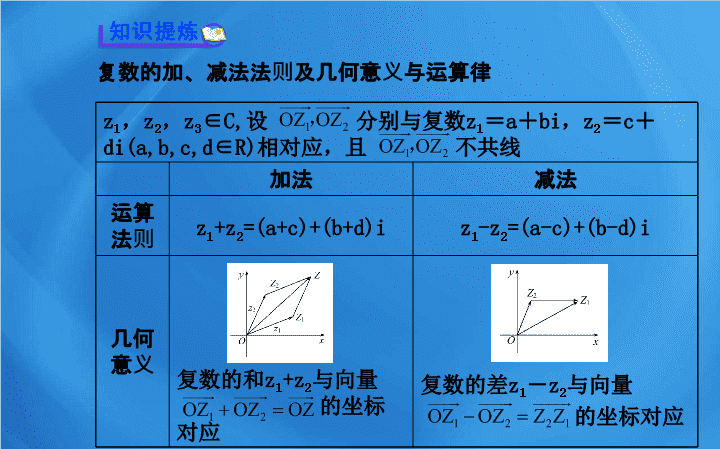
3.2 复数代数形式的四则运算 3.2.1 复数代数形式的加减运算及其 几何意义 问题 引航 1. 复数的加法、减法如何进行 ? 复数加法、减法的几何意义如何 ? 2. 复数的加减法与向量间的加减运算是否相同 ? 复数的加、减法法则及几何意义与运算律 z 1 ， z 2 ， z 3 ∈ C, 设 分别与复数 z 1 ＝ a ＋ bi ， z 2 ＝ c ＋ di(a,b,c,d ∈ R) 相对应，且 不共线 加法 减法 运算 法则 z 1 +z 2 =(a+c)+(b+d)i z 1 -z 2 =(a-c)+(b-d)i 几何 意义 复数的和 z 1 +z 2 与向量 的坐标 对应 复数的差 z 1 － z 2 与向量 的坐标对应 z 1 ， z 2 ， z 3 ∈ C, 设 分别与复数 z 1 ＝ a ＋ bi ， z 2 ＝ c ＋ di(a,b,c,d ∈ R) 相对应，且 不共线 加法 减法 运 算 律 交换律 z 1 +z 2 =z 2 +__ 结合律 (z 1 +z 2 )+z 3 =z 1 +(_____) z 1 z 2 +z 3 1. 判一判 ( 正确的打 “ √ ” , 错误的打 “ × ” ) (1) 复数与向量一一对应 . 　 ( 　　 ) (2) 复数与复数相加减后结果只能是实数 . 　 ( 　　 ) (3) 因为虚数不能比较大小 , 所以虚数的模也不能比较大小 . 　 ( 　　 ) 【 解析 】 (1) 错误 . 复数与复平面上的点一一对应 , 则复数与以原点为起点的向量一一对应 , 而不是与向量一一对应 . (2) 错误 . 复数与复数相加相减后依然是复数 , 可能为实数 , 也可能为虚数 . (3) 错误 . 虚数的模是实数 , 实数可以比较大小 . 答案 : (1)× 　 (2)× 　 (3)× 2. 做一做 ( 请把正确的答案写在横线上 ) (1) 计算： (3+5i)+(3-4i)=_______. (2)(5-6i)+(-2-2i)-(3+3i)=________. (3) 已知向量 对应的复数为 2-3i, 向量 对应的复数 为 3-4i ，则向量 对应的复数为 ______. 【 解析 】 (1)(3+5i)+(3-4i)=6+i. 答案： 6+i (2) 原式 =(5-2-3)+(-6-2-3)i=-11i. 答案： -11i (3) 答案： 1-i 【 要点探究 】 知识点 1 复数的加法、减法运算 对复数加法、减法运算的五点说明 (1) 一种规定 : 复数的代数形式的加法法则是一种规定 , 减法是加法的逆运算 ; 特殊情形 : 当复数的虚部为零时 , 与实数的加法、减法法则一致 . (2) 运算律 : 实数加法的交换律、结合律在复数集中仍成立 . 实数的移项法则在复数中仍然成立 . (3) 运算结果 : 两个复数的和 ( 差 ) 是唯一确定的复数 . (4) 适当推广 : 可以推广到多个复数进行加、减运算 . (5) 虚数单位 i: 在进行复数加减运算时 , 可将虚数单位 i 看成一个字母 , 然后去括号 , 合并同类项即可 . 【 微思考 】 (1) 两个复数的和是个什么数 , 它的值唯一确定吗 ? 提示 : 仍然是个复数 , 是一个确定的复数 . (2) 若复数 z 1 ,z 2 满足 z 1 -z 2 >0, 能否认为 z 1 >z 2 ? 提示 : 不能 . 如 2+i-i>0, 但 2+i 与 i 不能比较大小 . 【 即时练 】 已知复数 z 1 =3+4i,z 2 =3-4i, 则 z 1 +z 2 = 　 ( 　　 ) A.8i B.6 C.6+8i D.6-8i 【 解析 】 选 B.z 1 +z 2 =3+4i+3-4i=(3+3)+(4-4)i=6. 知识点 2 复数加减运算的几何意义 对复数加减运算的两点说明 (1) 复数的加法 : 根据复数加法的几何意义知 , 两个复数的和就是两个复数对应向量的和所对应的复数 . (2) 复数的减法 : 根据复数减法的几何意义 , 两个复数的差就是两个复数对应向量的差所对应的复数 . 【 知识拓展 】 注意类比思想方法的运用 . 复数与向量有着天然的联系 , 要注意向量知识在复数学习中的催化作用 . 【 微思考 】 (1) 类比绝对值 |x-x 0 | 的几何意义 , 说明 |z-z 0 |(z,z 0 ∈C) 的几何意义 . 提示 : |z-z 0 |(z,z 0 ∈C) 的几何意义是复平面内点 Z 到点 Z 0 的距离 , 即 |ZZ 0 |=|z-z 0 |. (2) 既然复数的加减法可以按照向量加减法的运算法则来运 算，是不是就有 z 1 ＋ z 2 ＝ z 2 － z 1 ＝ 呢 ? 提示 : 因为复数的几何意义只是强调了复数与向量之间的对应 关系；式子 z 1 ＋ z 2 ＝ z 2 － z 1 ＝ 的左边是复 数，而右边是向量，因此不能说 z 1 ＋ z 2 与 z 2 － z 1 与 相等． 【 即时练 】 复数 z 1 =1+2i,z 2 =3+5i 分别对应复平面内 A,B 两点 , 则 A ， B 两点 的距离为 ___________. 【 解析 】 复数 z 1 =1+2i,z 2 =3+5i 分别对应复平面内 A,B 两点的 坐标为 (1 ， 2) ， (3 ， 5) ，则 |AB|= 答案： 【 题型示范 】 类型一 复数的加法、减法运算 【 典例 1】 (1) 若 z 1 =2+i,z 2 =3+ai, 复数 z 1 +z 2 所对应的点在实轴上 , 则 a= 　 ( 　　 ) A.-2 B.2 C.-1 D.1 (2) 计算 :①(1+2i)+(-2+i)+(-2-i)+(1-2i); ②1+(i+i 2 )+(-1+2i)+(-1-2i). 【 解题探究 】 1. 复数 z 1 +z 2 的值是多少 ? 实轴上的点所对应复数的虚部是多少 ? 2. 题 (2) 中①各小括号内的复数所对应的实部与虚部分别是多少 ?② 中的 i 2 等于多少 ? 【 探究提示 】 1.z 1 +z 2 =5+(a+1)i, 实轴上点的纵坐标为 0, 则实轴上的点所对应复数的虚部是 0. 2.① 各小括号内的复数所对应的实部分别是 1,-2,-2,1, 虚部分别是 2,1,-1,-2.② 中的 i 2 等于 -1. 【 自主解答 】 (1) 选 C. 由 z 1 +z 2 =5+(a+1)i 所对应的点在实轴上得 a=-1. (2)① 原式 =(1-2-2+1)+(2+1-1-2)i=-2. ② 原式 =1+(i-1)+(-1+2i)+(-1-2i)=(1-1-1-1)+(1+2-2)i=-2+i . 【 方法技巧 】 复数加减运算法则的记忆 (1) 复数的实部与实部相加减 , 虚部与虚部相加减 . (2) 把 i 看作一个字母 , 类比多项式加减中的合并同类项 . 【 变式训练 】 计算 :(1)(1+2i)+(3-4i)-(5+6i). (2)5i-[(3+4i)-(-1+3i)]. 【 解析 】 (1) 原式 =(4-2i)-(5+6i)=-1-8i. (2) 原式 =5i-(4+i)=-4+4i. 【 误区警示 】 注意运算格式及范围避免出错 (1) 在进行复数减法运算时要注意格式 , 两复数相减所得结果依然是一个复数 , 其对应的实部与虚部分别是两复数的实部与虚部的差 . 注意中间用 “ + ” 号 , 如 z 1 =a+bi,z 2 =c+di,z 1 -z 2 =(a-c)+(b-d)i, 而不是 z 1 -z 2 =(a-c)-(b-d)i. (2) 复数中出现字母时 , 首先要判断其是否为实数 , 再确定复数的实部与虚部 , 最后把实部与虚部分别相加 . 【 补偿训练 】 计算 (a+bi)-(2a-3bi)-3i(a,b∈R). 【 解析 】 原式 =(a-2a)+[b-(-3b)-3]i=-a+(4b-3)i. 类型二 复数的加法、减法运算的几何意义 【 典例 2】 (1) 在复平面内 , 平行四边形 ABCD( 顶点顺序为 ABCD) 的三个顶点 A,B,C 对应的复数分别是 1+3i,-i,2+i, 则点 D 对应的 复数为 　　　　　 . (2) 已知 z 1 ， z 2 ∈C ， |z 1 |=|z 2 |=1 ， |z 1 +z 2 |= 求 |z 1 － z 2 | ． 【 解题探究 】 1. 点 A,B,C 的坐标分别是多少？向量 与向量 是否相等？ 2. 由复数的几何意义可知， z 1 ,z 2 ,z 1 +z 2 在复平面上对应的点分 别为 Z 1 ,Z 2 ,Z ，则它们与原点构成了一个什么样的图形？ 【 探究提示 】 1. 顶点 A,B,C 的坐标分别是 (1 ， 3) ， (0 ， -1) ， (2 ， 1) ；由平行四边形 ABCD 知，向量 与向量 相等 . 2. 在复平面内画出图形可知为平行四边形 . 【 自主解答 】 (1) 设 D(x,y), 类比向量的运算知 所以有 复数－ i － (1+3i)=2+i － (x+yi) 得 x=3,y=5, 所以 D 对应的复数 为 3+5i. 答案： 3+5i (2) 设复数 z 1 ， z 2 ， z 1 +z 2 在复平面上对应的点分别为 Z 1 ， Z 2 ， Z ，由 |z 1 |=|z 2 |=1 知，以 OZ 1 ， OZ 2 为邻边的平行四边形是菱形， 在△ OZ 1 Z 中，由余弦定理，得 所以∠ OZ 1 Z=120° ，所以∠ Z 1 OZ 2 =60° ，因此，△ OZ 1 Z 2 是 正三角形，所以 |z 1 － z 2 |=|Z 2 Z 1 |=1 ． 【 延伸探究 】 若把题 (2) 中的条件“ |z 1 +z 2 |= ” 改为 “ |z 1 -z 2 |=1” ，则 |z 1 +z 2 | 等于多少？ 【 解析 】 设复数 z 1 ， z 2 在复平面上对应的点分别为 Z 1 ， Z 2 ，由 |z 1 |=|z 2 |=1 ， |z 1 -z 2 |=1 知，以 OZ 1 ， OZ 2 为邻边的平行四边形是 菱形 OZ 1 ZZ 2 ， OZ 为对角线，△ OZ 1 Z 2 为正三角形，由余弦定理， 得 |z 1 +z 2 | 2 =|z 1 | 2 +|z 2 | 2 -2|z 1 ||z 2 |cos∠OZ 1 Z ， 因为∠ Z 1 OZ 2 =60°, 所以∠ OZ 1 Z=120° ， 所以 |z 1 +z 2 |= 【 方法技巧 】 利用复数加减运算的几何意义解题的技巧及常见结论 (1) 技巧 : ① 形转化为数：利用几何意义可以把几何图形的变换转化成复数运算去处理． ②数转化为形：对于一些复数运算也可以给予几何解释，使复数作为工具运用于几何之中． (2) 常见结论：在复平面内， z 1 ， z 2 对应的点分别为 A ， B ， z 1 ＋ z 2 对应的点为 C ， O 为坐标原点，则四边形 OACB ： ①为平行四边形； ②若 |z 1 ＋ z 2 | ＝ |z 1 － z 2 | ，则四边形 OACB 为矩形； ③若 |z 1 | ＝ |z 2 | ，则四边形 OACB 为菱形； ④若 |z 1 | ＝ |z 2 | 且 |z 1 ＋ z 2 | ＝ |z 1 － z 2 | ，则四边形 OACB 为正方形． 【 变式训练 】 如图所示，平行四边形 OABC 的顶点 O ， A ， C 分别表示 0,3 ＋ 2i ，－ 2 ＋ 4i. 求： (1) 表示的复数 . (2) 对角线 表示的复数 . (3) 对角线 表示的复数． 【 解题指南 】 (1) 中注意向量的起点与终点 .(2) 注意把向量 用向量 表示 . (3) 借助向量的运算 【 解析 】 (1) 则 对应的复数为－ (3 ＋ 2i) ， 即－ 3 － 2i. (2) 所以 对应的复数为 (3 ＋ 2i) － ( － 2+4i) ＝ 5 － 2i. (3) 所以 对应的复数为 (3 ＋ 2i) ＋ ( － 2 ＋ 4i) ＝ 1 ＋ 6i. 【 补偿训练 】 复数 z 1 ＝ 1 ＋ 2i ， z 2 ＝－ 2 ＋ i ， z 3 ＝－ 1 － 2i ，它们在复平面上的对应点是一个正方形的三个顶点，求这个正方形的第四个顶点对应的复数． 【 解析 】 设复数 z 1 ， z 2 ， z 3 在复平面内所对应的点分别为 A ， B ， C ，正方形的第四个顶点 D 对应的复数为 x ＋ yi(x ， y∈R) ，如图． 则 ＝ (x ＋ yi) － (1 ＋ 2i) ＝ (x － 1) ＋ (y － 2)i ， ＝ ( － 1 － 2i) － ( － 2 ＋ i) ＝ 1 － 3i. 因为 所以 (x － 1) ＋ (y － 2)i ＝ 1 － 3i. 所以 解得 故点 D 对应的复数为 2 － i. 【 易错误区 】 复数运算中思维不严谨而致误 【 典例 】 设 x∈[0,2π), 复数 z 1 =cosx+isinx 对应的点在第 一象限中直线 y=x 的左上方 ,z 2 =1-i, 则 |z 1 +z 2 | 的取值范围是 　　　　 . 【 解析 】 由已知得 z 1 +z 2 =(cos x+1)+(sin x-1)i ， 所以 |z 1 +z 2 |= 因为复数 z 1 =cos x+isin x 对应的点在第一象限中直线 y=x 的左上方，且 x∈ ［ 0,2π) ， 所以 解得 所以 故 所以 答案： 【 常见误区 】 错解 错因剖析 忽视阴影处 x 的取值范围，想当然地认为 x 可以取［ 0,2π) 范围内的任意实数 , 从 而 cos （ x+ ）的范围是［ -1,1 ］，故 得错误的结果为 【 防范措施 】 1 ．题目条件的充分利用 解题时，要仔细审题，建立条件与所求之间的联系，实现题目条件向结论的正确转化，如本例根据已知条件，将 |z 1 +z 2 | 化为三角函数式，再化简求值 . 2. 注意条件的挖掘 已知复数 z=a+bi, 根据复数的几何意义，已知点的坐标所在位置，可得 a,b 的取值范围，如本例中根据 z 1 对应的点的位置可列不等式组，得到 x 的取值范围 . 【 类题试解 】 若复数 z 1 =2cos α+isin α,z 2 =cos α- (sin α-1)i,α∈(0,π), 且 z 1 -z 2 ＜ 0, 则 α=_________. 【 解析 】 由条件得 z 1 -z 2 =cos α+(2sin α-1)i, 因为 z 1 -z 2 ＜ 0, 所以 由 2sin α-1=0, 得 sin α= 又 α∈(0,π), 所以 当 α= 时， cos α= ＞ 0, 故舍去 , 所以 答案：