【数学】2018届一轮复习人教A版集合与常用逻辑用语教案 10页

2018 年高考数学（理）一轮复习讲义：集合与常用逻 辑用语 一、考点突破 本讲涉及考点主要包括：元素与集合；集合间的关系；集合的基本运算；集合运算的基 本性质；逻辑连接词“且、或、非”的概念；命题与充要条件． 课标的具体要求是： 1. 了解集合的含义、元素与集合的属于关系． 2. 理解集合之间包含与相等的含义，能识别给定集合的子集． 3. 理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集． 4. 能使用韦恩（Venn）图表达集合的关系及运算． 5. 了解逻辑连接词“或”、“且”、“非”的含义． 6. 能正确地对含有一个量词的命题进行否定． 7. 了解“若 p 则 q”形式的命题的逆命题、否命题与逆否命题，会分析四种命题的相互 关系． 8. 理解必要条件、充分条件与充要条件的意义． 纵观近一两年年高考试题，本讲知识没有单独的题目，而是把集合与逻辑的思想贯穿于 其他题目中，大多有 1~2 个小题（选择或填空），基本为简单题，以集合与逻辑为背景命制 选择题的压轴题是一个新的特点． 二、重难点提示 1. 求两个简单集合的并集与交集；求给定子集的补集． 2. 判断必要条件、充分条件与充要条件． 3. 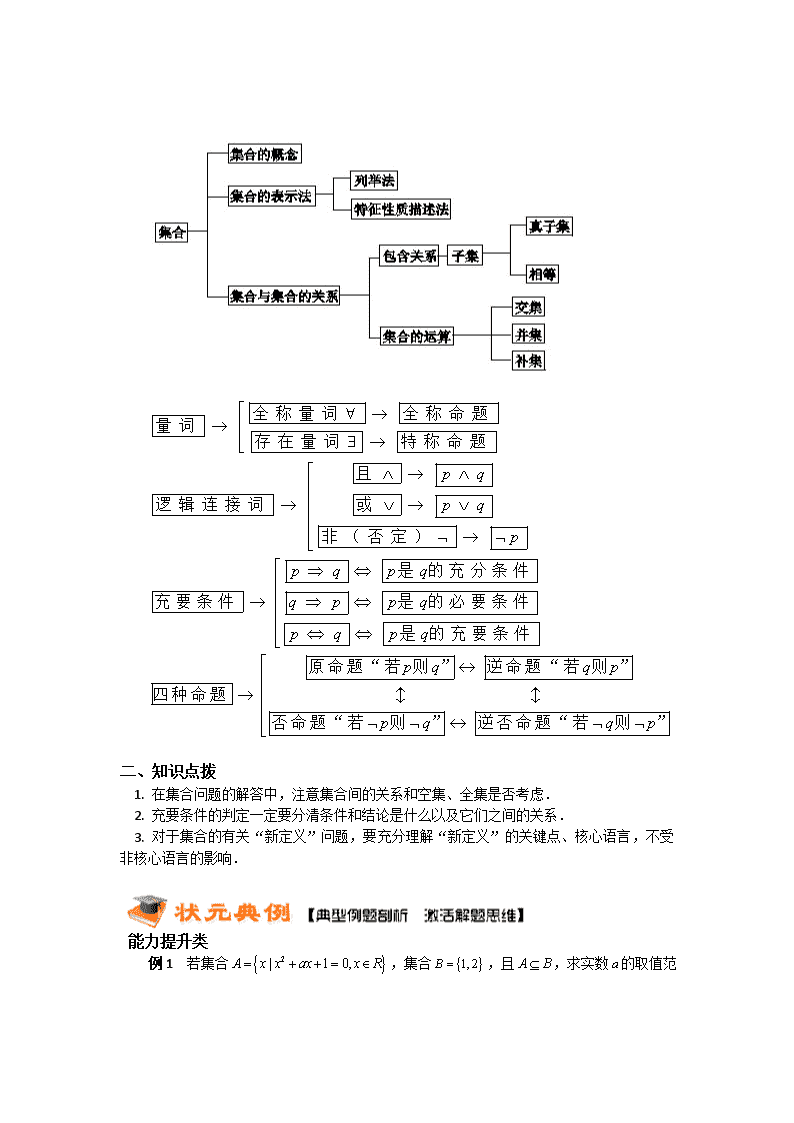写出简单命题的逆命题、否命题与逆否命题，分析四种命题的相互关系；正确地对含 有一个量词的命题进行否定． 一、知识脉络图 二、知识点拨 1. 在集合问题的解答中，注意集合间的关系和空集、全集是否考虑． 2. 充要条件的判定一定要分清条件和结论是什么以及它们之间的关系． 3. 对于集合的有关“新定义”问题，要充分理解“新定义”的关键点、核心语言，不受 非核心语言的影响． 能力提升类 例 1 若集合 ，集合 ，且 ，求实数 的取值范 p q p q p  ∀ →→  ∃ →  ∧ → ∧  → ∨ → ∨  ¬ → ¬ 全 称 量 词 全 称 命 题量 词 存 在 量 词 特 称 命 题 且 逻 辑 连 接 词 或 非 （ 否 定 ） p q p q q p p q p q p q  ⇒ ⇔ → ⇒ ⇔  ⇔ ⇔ 是 的 充 分 条 件 充 要 条 件 是 的 必 要 条 件 是 的 充 要 条 件 p q q p p q q p  ↔ →   ¬ ¬ ↔ ¬ ¬   原 命 题 “ 若 则 ” 逆 命 题 “ 若 则 ” 四 种 命 题 否 命 题 “ 若 则 ” 逆 否 命 题 “ 若 则 ” { }2| 1 0,A x x ax x R= + + = ∈ { }1,2B = A B⊆ a 围． 一点通：由 可知，A 的可能情况为四种，分别针对 A 的各种情况，来考虑方程的 解的情况，则不难得出相应的 a 的取值范围。注意 的情况． 分 四种情况（有些无解）讨论． 答案： ． ∵A 是 B 的子集， 故知集合 A 可能为 ，{1}，{2}，{1，2}， 由根与系数的关系可知 ，知 及 均不可能，因而 或 。 当 时，即方程 没有实数解，故知 ，即 。 当 时，即方程有两个相等的根 1，由根与系数的关系可知， ，即 。 综上所述，所求 的范围是 。 点评：（1）分类讨论一定要注意分类标准的统一和前后一致；本题中，可以按集合中 元素的个数来分类，即按元素个数为 0、1、2 分为三类． （2）注意空集、端点是否可以取得，本题中 不合题意． 例 2 已 知 为 全 集 ， ， 求 ． 一点通：熟悉常见不等式的解法，注意在比较对数大小时，把任意一个数写成对数的形 式 ： ， 这 里 ， 还 要 注 意 对 数 函 数 的 定 义 域 ， 可 求 得 ． 答案： ． 点评：（1）比较大小是各类考试常见题型，要注意定义域和单调性，合理应用不等式 的性质． （2）注意把要比较的数或式分类：正与负；正数中大于 1 与小于 1；负数中是否小于 -1． （3）求补集时，要注意是求在哪一个集合中的补集． 综合运用类 例 3 集合 ，A 是 S 的一个子集，当 时，若有 且 ， 则称 为 A 的一个“孤立元素”，写出 S 的无“孤立元素”的四元子集． 一点通：分类讨论：无“孤立元素”的四元子集可分为两类：一类是四个连续的数字； 另一类是四个元素分为两组，每一组的两个数字为相邻的数字． 答案： ， ． 将 S 的 4 元子集 A 按从小到大的次序排列 A={a，b，c，d}．A 没有孤立元素，那么如果 a=0 或者 d=5，必须 b=1 或者 c=4，否则 0 或 5 就是孤立元素。a=0，b=1 时，如果没有孤立 2a = A B⊆ A = ∅ { } { } { }1 ; 2 ; 1,2 ;A A A A= = = = ∅ [ )2,2− ∅ 121 =⋅ xx }2{=A }2,1{=A ∅=A }1{ ∅=A 012 =++ axx 042 <−a 22 <<− a }1{=A a−=+11 2−=a a )2,2[− R }2)3(log|{},2)3)(3(log|{ 3 1 3 1 −≥−=−−−= xxAxxxA }12 5|{ ≥+= xxB B)AC( R ∩ log N aN a= 2 1 3 12 log 3 − − =    [ ) ( ]6,3 ; 2,3A B= − = − { }( ) 3RC A B = { }0,1,2,3,4,5S = x A∈ 1x A− ∉ 1x A+ ∉ x { }0,1,2,3 { }1,2,3 4， { }2,3 4,5， { }0,1,3 4， { }0,1,4,5 { }1,2,4,5 元素，c，d 必须是相连的数字。有 3 种方法取 c，d。同样如果 c=4，d=5，也有 3 种方法去 a，b。考虑到重复计算的一种，所以有 5 种办法去取 a，b，c，d 使 a=0 或者 d=6，而且没 有孤立元素。如果 a 0，d 4．则只有 。因此总共无孤立元素的 4 元子集有 6 个。 它们是：{0，1，2，3}，{0，1，3，4}{0，1，4，5}{1，2，4，5}{2，3，4，5}{1，2，3，4} 点评：（1）分类讨论是解决集合问题的重要的方法，分类时一定要注意有一个统一的 分类标准． （2）注意全面考察问题，不要漏掉每一种可能的情况． 例 4 已知： 若 是 的充分而不必要条件，求 的取值范围． 一点通：本题有两种解题思路：一是把 和 分别用集合表示出来，然后根据充分而 不必要条件与子集的关系得到结果；二是直接用 和子集关系得到结果． ； ． 答案： ． 点评：（1）解答充要条件与集合的问题时，一定要搞清楚条件与集合中真子集和子集 的关系，充分不必要条件对应真子集，充分条件对应子集，充要条件对应集合相等． （2）注意从多角度考察问题，把四种命题及其关系恰当地运用到集合问题中，例如 ． 思维拓展类 例 5 若命题 x2+ax+1<0“ ”是真命题，求实数 a 的取值范围． 一点通：注意 和 的区别与联系，前者是求 的最小 值问题，后者是求 的最大值问题．故该命题可等价为 ． 答案： ． 点评：（1）在讨论有关命题的问题中，一定要分清条件中是“恒成立”还是“能成 立”，即分清其是全称命题还是特称命题，它们的标志是“对任意 ”和“存在 ”． （2）等价转换是数学解题的关键，完成转换的条件是对题目的全面理解和对数学知识 的“有机联想”．比如：二次函数 恒成立 ； 能成立 ． 例 6 下列四个命题中，真命题有________（写出所有真命题的序号） ① ； ②若 ，则 ； ③ ， 与 均为非负数； ④命题“存在奇数 ，使得 被 4 除，余数不等于 1 或 3”的否定． 一点通：这是一道很常见的试题，对于②你能想到多少种解法？ 命题②的证明思路: 思路一:证明它的逆否命题; ∀ ∃ 2( ) 0( 0)f x ax bx c a= + + > > 2 4 0b ac⇔ ∆ = − < 2( ) 0( 0)f x ax bx c a= + + < > 2 4 0b ac⇔ ∆ = − > ≠ ≠ { }1,2,3,4 ( )2 2: 4 6, : 2 1 0 0 ,p x q x x a a− ≤ − + − ≥ > p¬ q a p¬ q " " " "p q q p¬ ⇒ ⇔ ¬ ⇒ : 4 6 :| 4 | 6 2 10p x p x x x− ≤ ⇒ ¬ − > ⇔ < − >或 ( )2 2: 2 1 0 0 1 1q x x a a x a x a− + − ≥ > ⇔ ≤ − ≥ +或 (0,3]p q a¬ ⇒ ⇒ ∈ p q q p⇒ ⇔ ¬ ⇒ ¬“ ” “ ” 2, 1 0x R x ax∃ ∈ + + <使 , ( ) 0x R f x∃ ∈ <使 , ( ) 0x R f x∀ ∈ <使 ( )f x ( )f x 2 4 0a∆ = − > ( ) ( ), 2 2,−∞ − +∞ 77 ≥ 222 =+ qp 22 ≤+≤− qp Rba ∈∀ , 22 baba ++ 22 baba +− )0( >nn n 思路二:利用不等式; ‘思路三:换元法; 思路四:三角换元; 思路五:利用向量的数量积. 答案：① 或 ，故①为真命题； ②为真命题，证明如下： 证法一：证明它的逆否命题：“若 或 ，则 ”． 由 或 ，得 。所以 。 证法二：由 ，得 ， ，即 。 证法三：设 ，则 ， ， 由 ，得 ，解得 ，即 。 证法四：设 ，则 ， 又 ，得 。 证法五：设向量 ，由 ，得 ，即 。 ③ ， ， 同理可证 ，故正确。 ④命题的否定为：“对任意的奇数 ，使得 被 4 除，余数等于 1 且 3”。因为 任意奇数 被 4 除，余数等于 1 或 3，不可能既等于 1 又等于 3。故④不正确。 所以，真命题的序号有①②③。 点评：此题的亮点在于对于命题②的判断，有多种方法，通过对不同解法的探讨可以让 学生掌握数学思想方法的应用． 例 3 已 知 集 合 对 于 ， ， 定 义 A 与 B 的 差 为 A 与 B 之间的距离为 （Ⅰ）当 n=5 时，设 ，求 ； （Ⅱ）证明： ，且 ； （Ⅲ）证明： 三个数中至少有一个是偶数． 一点通： 答案： （Ⅰ）解： =（1，0，1，0，1） 7777 >⇔≥ 77 = 2−<+ qp 2>+ qp 222 ≠+ qp 2−<+ qp 2>+ qp 222 1)(2 1])()[(2 1 222222 =×>+≥++−=+ qpqpqpqp 222 ≠+ qp 222 qppq +≤ 2222 222 qppqqp +≤++ 4)(2)( 222 =+≤+∴ qpqp 22 ≤+≤− qp tqp =+ 222 2 tpqqp =++ 22 2 −= tpq pqqp 222 ≥+ 222 ≤−t 22 ≤≤− t 22 ≤+≤− qp θθ sin2,cos2 == qp )sin(2)cos(sin2 ϕθθθ +=+=+ qp 1)sin(1 ≤+≤− ϕθ 22 ≤+≤− qp ),(),1,1( qpba == |||||,cos||||||| babababa ⋅≤><⋅⋅=⋅ 22|| 22 =+⋅≤+ qpqp 22 ≤+≤− qp Rba ∈∀ , 04 3)2( 2222 ≥++=++ bbababa 022 ≥+− baba )0( >nn n n 1 2{ | ( , , ), {0,1}, 1,2, , }( 2)n n iS X X x x x x i n n= = ∈ = ≥… ， … 1 2( , , )nA a a a= … 1 2( , , ,)n nB b b b S= ∈… 1 1 2 2(| |,| |, | |);n nA B a b a b a b− = − − −… 1 ( , ) | | n i i i d A B a b = = −∑ (0,1,0,0,1), (1,1,1,0,0)A B= = ( , )d A B , , ,n nA B C S A B S∀ ∈ − ∈有 ( , ) ( , )d A C B C d A B− − = , , , ( , ), ( , ), ( , )nA B C S d A B d A C d B C∀ ∈ 0 1 i i i i i i a ba b a b =− =  ≠ ( 0 1 , 1 1 , 0 1 , 0 0 , 1 0 )A B− = − − − − − =3． (Ⅱ)证明：设 因为 ，所以 从而 由题意知 当 时， 当 时， 所以 (Ⅲ)证明：设 记 ，由（Ⅱ）可知 所以 中 1 的个数为 k， 中 1 的个数为 ， 设 是使 成立的 的个数，则 ， 由此可知， 三个数不可能都是奇数，即 三个数中至少有一 个是偶数． 点评：（1）本题属于新概念及应用新概念解决问题的题型，对学生分析问题、解决问 题的能力要求很高，要在深刻理解题意的基础上灵活解决问题． （2）（Ⅰ）、（Ⅱ）考查的是对概念的准确理解，可以直接应用概念解决问题，（Ⅲ）可 以考虑用反证法． 1. 集合与命题、集合与充要条件、命题与充要条件的关系要理解到位：一个命题是真命 题，条件是结论的充分条件；一个命题的逆命题是真命题，条件是结论的必要条件．集合中 的真子集对应充分不必要条件；子集对应充分条件等． 2. 对含有一个量词的命题的否定，要掌握其基本格式：命题： 的否定： ；命题： 的否定： ． 1. 弄清命题是全称命题还是特称命题是正确写出命题否定的关键，要注意命题的否定与 否命题的关系，当命题 p 的真假不好判断时，可以考虑判断非 p 的真假，当原命题的真假不 好判断时，可以考虑判断其逆否命题的真假． 2. 充要条件的判定是本讲的重点，要十分重视充要条件和命题的关系与集合的包含关系 之间的联系． , ( )x M p x∀ ∈ 0 0, ( )x M p x∃ ∈ ¬ 0 0, ( )x M p x∃ ∈ , ( )x M p x∀ ∈ ¬ ( , ) 0 1 1 1 0 1 0 0 1 0d A B = − + − + − + − + − 1 2 1 2 1 2( , , , ), ( , , , ), ( , , , )n n n nA a a a B b b b C c c c S= ⋅⋅⋅ = ⋅⋅⋅ = ⋅⋅⋅ ∈ , {0,1}i ia b ∈ {0,1}( 1,2, , )i ia b i n− ∈ = ⋅⋅⋅ 1 1 2 2( , , )n n nA B a b a b a b S− = − − ⋅⋅⋅ − ∈ , , {0,1}( 1,2, , )i i ia b c i n∈ = ⋅⋅⋅ 0ic = i i i i i ia c b c a b− − − = − 1ic = (1 ) (1 )i i i i i i i ia c b c a b a b− − − = − − − = − 1 ( , ) ( , ) n i i i d A C B C a b d A B = − − = − =∑ 1 2 1 2 1 2( , , , ), ( , , , ), ( , , , )n n n nA a a a B b b b C c c c S= ⋅⋅⋅ = ⋅⋅⋅ = ⋅⋅⋅ ∈ ( , ) , ( , ) , ( , )d A B k d A C l d B C h= = = 0 (0,0, 0) nS= ⋅⋅⋅ ∈ ( , ) ( , ) (0, ) ( , ) ( , ) (0, ) ( , ) ( , ) d A B d A A B A d B A k d A C d A A C A d C A l d B C d B A C A h = − − = − = = − − = − = = − − = ( 1,2, , )i ib a i n− = ⋅⋅⋅ ( 1,2, , )i ic a i n− = ⋅⋅⋅ l t 1i i i ib a c a− = − = i 2h l k t= + − , ,k l h ( , ), ( , ), ( , )d A B d A C d B C （答题时间：60 分钟） 一、选择题： 1. 方程 有一个实根是 的 条件 A. 充要 B. 充分不必要 C. 必要不充分 D. 既不必要也不充分 2. 同时满足（1） （2）若 则 的非空集合 M 有 A. 16 个 B. 15 个 C. 7 个 D. 6 个 3. 集合 ，则 A. 　　　B. 　　　C. 　　　D. 4. 已知集合 ， ， 则 的值为 A. 4 B. 3 C. 2 D. 1 5. 已知 则使 成立的一个充分条件是 A. B. C. D. 6. 已知命题 ： ， ；命题 ： ．则下列结论正确 的是 A. 命题 是真命题 B. 命题 是真命题 C. 命题 是真命题 D. 命题 是假命题 7．（江苏高考）设集合 , , 若 则实数 m 的取值范围是 ______________ 8.(广东高考).设 是整数集 的非空子集，如果 有 ，则称 关于数的乘法是封闭的. 若 , 是 的两个不相交的非空子集， 且 有 有 ，则下列结论恒成立的是 A． 中至少有一个关于乘法是封闭的 B. 中至多有一个关于乘法是封闭的 C. 中有且只有一个关于乘法是封闭的 D. 中每一个关于乘法都是封闭的 9.（陕西高考）设集合 M={y|y= x— x|,x∈R},N={x||x— |< ,i 为虚数单位，x∈R}, 则 M∩N 为 A．（0,1） B．（0,1] C．[0,1） D．[0,1] 二、填空题 10. 若 ， 命 题 “ 是 偶 数 ， 则 必 定 同 为 奇 数 或 偶 数 ” 的 逆 否 命 题 },,)2(2|),{( 222 RyxmyxmyxA ∈≤+−≤= },,122|),{( RyxmyxmyxB ∈+≤+≤= ,φ≠∩ BA , ,a b S∀ ∈ ab S∈ , , ,a b c T∀ ∈ xyz V∈ ,T V ,T V ,T V ,T V 2cos 2sin 1 i 2 2 3 1 0ax x+ − = 9 4a = − { }1.2.3.4.5M ⊆ a M∈ 6 a M− ∈ { } { }2( , ) 1 , , R , ( , ) 1, RM x y y x x y N x y x y= = − ∈ = = ∈ M N = { }(1,0) { }0 1y y≤ ≤ { }1,0 ∅ { } { }2| 2 3 0 , | ,A x x x B x x a b A B R= − − > = − ≤ =若 { }| 3 4A B x x= < ≤ a b+ , , ,a b c R∈ a b> ac bc> c b c a > 2 2 a b c c > 2 2a b> p x R∃ ∈ 5cos 4x = q 2, 1 0x R x x∀ ∈ − + > p q且 p q¬且 p q¬ 且 p q¬ ¬或 S Z S T V Z T V Z= ; , , ,abc T x y z V∈ ∀ ∈ ,a b Z∈ a b+ ,a b 为 ． 11. 设 若 ，则 ． 12. 设全集 ，则 ． 13. 用列举法表示集合 ． ______________ 三、解答题： 14. 已 知 集 合 T 是 方 程 的 解 集 ， ，且 ，试求 的值． 15. 设 ，若 ，求实数 的取值范 围． 16. 已知集合 ，若 ， 求实数 的取值范围． 17. 已知命题 q：集合 ， ，则 ． （Ⅰ）若命题 q 为真命题，求实数 a 的取值范围； （Ⅱ）若命题 p: ， ，试求实数 a 的取值范围，使得命题 p，q 有 且只有一个为真命题． { } { }21,2,3,4 | 5 0S M x S x x p= = ∈ − + =且 { }1,4SC M = p = { } { } { }2,3,5 , 5 ,2 , 5UU A a C A= = − = a = | , , , ,a b c abcM x x a b c R Ma b c abc   = = + + + ∈ =    则 2 20( 4 0)x px q p q+ + = − > { } { }1,3,5,7,9 , 1,4,7,10A B= = T A T B T= ∅ = ， ,p q { } { }2 2| 4 0 , |M x x N x x ax x a= − > = − ≥ − M N M= a { } ( ){ }2| 1 , | 3 3 0,M x x a N x x a x a a R= − < = − + + > ∈ M N R= a { }2| 1 0,A x x ax x R= + + = ∈ { }| 0B x x= > A B = ∅ 1( ) 2 xf x −= ( ) 2f a < 一、选择题: 题 号 1 2 3 4 5 6 答 案 C C A A C C 7.当 时，集合 A 是以（2，0）为圆心，以 为半径的圆，集合 B 是在两条平行线之 间， ，因为 此时无解；当 时， 集合 A 是以（2，0）为圆心，以 和 为半径的圆环，集合 B 是在两条平行线之间，必 有 .又因为 8.A;因为 ,故必有 或 ,不妨设 ,则令 ,依题意对 , 有 ,从而 关于乘法是封闭的;(其实到此已经可以选 A 了,但为了严谨,我们往下 证明可以有一个不封闭以及可以两个都封闭),取 ,则 为所有负整数组成的集合, 显然 封闭,但 显然是不封闭的,如 ;同理,若 奇数 ， 偶数 ，显然两者都封闭，从而选 A． 9. C ，所以 ； 因为 ，所以 ，即 ，又因为 R，所以 ， 即 ；所以 ，故选 C. 二、填空题 10. 已知 ，若 一个是偶数，一个是奇数，则 不是偶数； 11.6； 12.8 或 2； 13. ． 三、解答题 14. ，由韦达定理可得： ． 15. ， ，由 ，故 a 的取 值范围是 ． 16. ， ， 0m ≤ m 2 2 1 2(1 2) 022 m m m − − + = − + > ,φ≠∩ BA 0m > 2 m m 2 2 1 2 2 2 2 m m m m − − ≥ − ≤   2 1 2 12 m −∴ ≤ ≤ + 2m 1, 2 12 2m m≤ ∴ ≤ ≤ + T V Z= 1∈ T 1∈V 1∈ T 1c = ,a b T∀ ∈ ab T∈ T T N= V T V ( 1) ( 2) 2 V− × − = ∉ {T = } {V = } 2 2| cos sin | | cos2 | [0,1]y x x x= − = ∈ [0,1]M = 1| | 2x i − < | | 2x i+ < | ( ) | 2x i− − < x∈ 1 1x− < < ( 1,1)N = − [0,1)M N = ,a b Z∈ ,a b a b+ { }4,0,4− { }4,10T = 14; 40p q= − = { }| 2 2M x x x= < − >或 { }| ( )( 1) 0N x x a x= − − ≥ M N M M N= ⇒ ⊆ [ ]2,2− { }| 1 1M x a x a= − < < + { }| ( )( 3) 0N x x a x= − − > 由 ． 17. （Ⅰ）即方程 无根或无正根 ； （ Ⅱ ） ， 结 合 （ Ⅰ ） 可 得 a 的 取 值 范 围 是 ． 1 3 2 41 3 aM N R aa − <= ⇒ ⇒ < < + > 2 1 0x ax+ + = 2 4 0 0a a− < − <或 ( )2,a⇒ ∈ − +∞ 1( ) 2 2 3 52 af a a −< ⇒ < ⇒ − < < ( ] [ )3, 2 5,− − +∞