高中数学选修2-2课时练习第四章 章末复习 7页

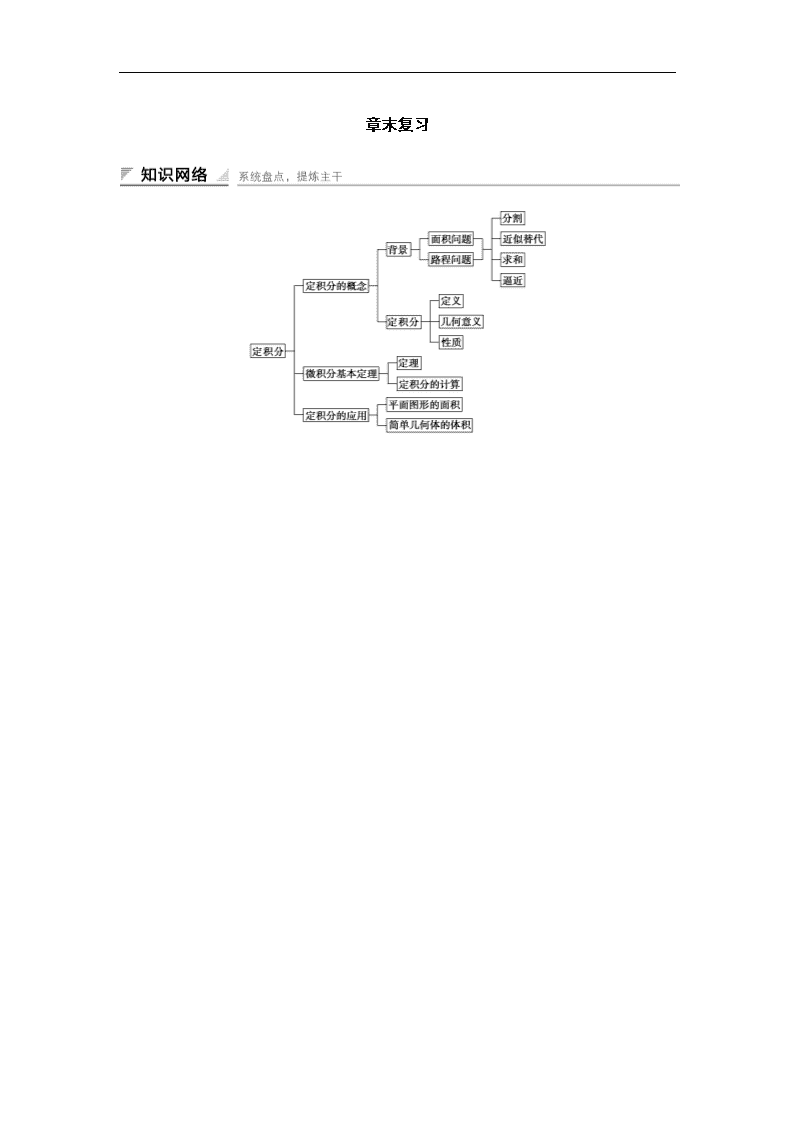
章末复习 ‎1．定积分概念的理解 由定义可得定积分f(x)dx是一个常数，它的值仅仅取决于被积函数与积分的上、下限，而与积分变量用什么字母表示无关，即f(x)dx＝f(u)du＝f(t)dt＝……‎ ‎2．运用微积分基本定理计算定积分f(x)dx的关键是找到满足F′(x)＝f(x)的函数F(x)．通常我们运用基本初等函数的求导公式和导数的四则运算法则从反方向上求出F(x)．‎ ‎3．由微积分基本定理理解定积分的几何意义 ‎(1)当对应的曲边梯形位于x轴上方时，定积分的值取正值，且等于曲边梯形的面积．‎ ‎(2)当对应的曲边梯形位于x轴下方时，定积分的值取负值，且等于曲边梯形的面积的相反数．‎ ‎(3)‎ 当位于x轴上方的曲边梯形的面积等于位于x轴下方的曲边梯形的面积时，定积分的值为0(如图)，且等于位于x轴上方的曲边梯形面积减去位于x轴下方的曲边梯形面积．‎ 题型一　由定积分的几何意义求定积分 定积分的求解问题，通常利用定积分的几何意义转化为求一个图形的面积问题，正确地作出被积函数的图像，然后由求面积的方法求解该定积分是解决本类问题的重点．‎ 例1　‎ 根据定积分的几何意义计算定积分|x－2|dx.‎ 解　根据定积分的几何意义，所求定积分表示的是y＝|x－2|和x＝3，x＝1及y＝0所围成的图形的面积，即图中阴影部分面积．‎ 因此，|x－2|dx＝×1×1＋×1×1＝1.‎ 跟踪演练1　定积分(－x)dx等于(　　)　　　　　　　　　　　　　　　　　　　‎ A. B.－1‎ C. D. 答案　A 解析　(－x)dx＝dx－xdx.dx表示圆(x－1)2＋y2＝1的上半圆与x＝1，x＝0，y＝0围成的图形面积．‎ 画出图形可知S1＝dx＝，‎ ‎∴S＝S1－S2＝.‎ 题型二　利用微积分基本定理求定积分 利用微积分基本定理计算定积分与定义法计算定积分相比较，使运算量大大地减少了，因此在计算定积分时要优先考虑微积分基本定理的运用．‎ 利用微积分基本定理求定积分关键是要找到被积函数的原函数，在找被积函数的原函数时，一定要仔细观察被积函数的结构，结合导数公式和导数的运算性质，才能较快地找到原函数．‎ 例2　计算下列定积分：‎ ‎(1) cos2dx；(2) |x2－x|dx.‎ 解　(1) cos2dx＝dx ‎＝ (1＋cos x)dx ‎＝ ＝＝＋.‎ ‎(2) |x2－x|dx＝ (x2－x)dx＋(x－x2)dx＋‎ (x2－x)dx＝＋＋＝.‎ 跟踪演练2　计算下列定积分：‎ ‎(1) dx；(2)dx.‎ 解　(1) ‎ ‎＝＝12；‎ ‎(2)dx ‎＝dx＋dx ‎＝dx＋dx ‎＝＋＝.‎ 题型三　定积分的应用 ‎1．定积分可用来计算曲边梯形的面积，某些曲面面积可以表示成几个曲边梯形面积的和或差的形式．‎ ‎2．利用定积分也可以求出一些简单的几何体体积，如圆锥体、圆柱体、圆台、球体等．计算由曲线y＝f(x)，直线x＝a，x＝b及x轴所围成的曲边梯形绕x轴旋转一周而生成的旋转体的体积为V＝π[f(x)]2dx.‎ 例3　(1)求由曲线y＝sin x，y＝cos x及直线x＝0，x＝所围成图形的面积．‎ ‎(2)求抛物线y2＝2px(p>0)与直线x＝p及x轴所围成的图形绕x轴旋转一周所得旋转体的体积．‎ 解　(1)先画草图如图．‎ 其次，若选x为积分变量，积分下限为x＝0，上限为x＝.最后，‎ 由图形可知，平面图形由x＝把图形分成两块．‎ A＝|sin x－cos x|dx ‎＝ (cos x－sin x)dx＋ (sin x－cos x)dx ‎＝ ＋ ‎＝2(－1)．‎ ‎(2)如图所示，因为y2＝2px(p>0)，‎ 所以[f(x)]2＝2px，x∈.‎ 所以V＝π [f(x)]2dx ‎＝π2pxdx＝ ＝.‎ 跟踪演练3　(1)求曲线y＝sin x，x∈[0，π]与x轴所围成平面图形绕x轴旋转一周所得到旋转体的体积．‎ ‎(2)如图所示，求由抛物线y＝－x2＋4x－3及其在点A(0，－3)和点B(3,0)处的切线所围成的图形的面积．‎ 解　(1)由体积公式V＝πy2dx＝π(sin x)2dx ‎＝πsin2xdx＝πdx ‎＝π ‎＝(1dx－cos 2xdx)‎ ‎＝ ‎＝(π－0)＝.‎ ‎(2)由题意，知抛物线y＝－x2＋4x－3在点A处的切线斜率是k1＝4，在点B处的切线斜率是k2＝－2.因此，抛物线过点A的切线方程为 y＝4x－3，过点B的切线方程为y＝－2x＋6.‎ 设两切线相交于点M，由 消去y，得x＝，即点M的横坐标为.‎ 在区间上，曲线y＝4x－3在曲线y＝－x2＋4x－3的上方；在区间上，曲线y＝－2x＋6在曲线 y＝－x2＋4x－3的上方．‎ 因此，所求的图形的面积是：‎ S＝ [(4x－3)－(－x2＋4x－3)]dx＋‎ ‎ [(－2x＋6)－(－x2＋4x－3)]dx ‎＝x2dx＋ (x2－6x＋9)dx＝＋＝.‎ ‎1．了解定积分概念的背景知识及概念的产生过程和其蕴含的数学思想是本章的重要内容，与定积分的几何意义和物理意义相结合更能体现定积分的实用价值，也有利于理解概念．‎ ‎2．利用牛顿—莱布尼茨公式求定积分是本章的另一个核心内容，也是学好本章的基础．一方面要明确微积分基本定理揭示了原函数与其导函数的关系，并掌握利用导数公式表，由导函数逆推得到原函数的方法．另一方面要熟练应用一些常见的定积分的性质．‎ ‎3．微积分基本定理，实际上给出了微分与积分之间的联系，在解决含有参数的定积分问题时，往往要对字母参数进行讨论，有时解决这类问题要与其他知识联系起来，综合解决．‎