【数学】江西省南昌市八一中学2019-2020学年高二下学期期末考试（文） 9页

江西省南昌市八一中学2019-2020学年高二下学期期末考试（文）‎ 一、选择题（本大题共12小题，共60.0分）‎ 1. 设复数z满足，则    ‎ A. 1 B. C. D. 2‎ 2. 为研究语文成绩和英语成绩之间是否具有线性相关关系，统计两科成绩得到如图所示的散点图两坐标轴单位长度相同，用回归直线近似地刻画其相关关系，根据图形，以下结论最有可能成立的是 ‎ A. 线性相关关系较强，b的值为 B. 线性相关关系较强，b的值为 C. 线性相关关系较强，b的值为 D. 线性相关关系太弱，无研究价值 3. 若m，n是两条不同的直线，，，是三个不同的平面，则下列命题中的真命题是   ‎ A. 若，，则 B. 若，，则 C. 若，，则 D. 若，，，则 4. 在正方体中，如图，M，N分别是正方形ABCD，的中心．则过点，M，N的截面是（ ） A. 正三角形 B. 正方形 C. 梯形 D. 直角三角形 5. 九章算术是中国古代张苍，耿寿昌所撰写的一部数学专著，成书于公元一世纪左右，内容十分丰富．书中有如下问题：“今有圆堢瑽，周四丈八尺，高一丈一尺，问积几何？答曰：二千一百一十二尺．术曰：周自相乘，以高乘之，十二而一．”这里所说的圆堢瑽就是圆柱体，它的体积底面的圆周长的平方高，则该问题中的体积为估算值，其实际体积单位：立方尺，一丈=10尺应为   ‎ A. B. C. D. ‎ 6. 从11，12，13，14，15中任取2个不同的数，事件“取到的2个数之和为偶数”，事件“取到的2个数均为偶数”，则等于      ‎ A. B. C. D. ‎ 7. 函数的图象大致为 A. B. C. D. 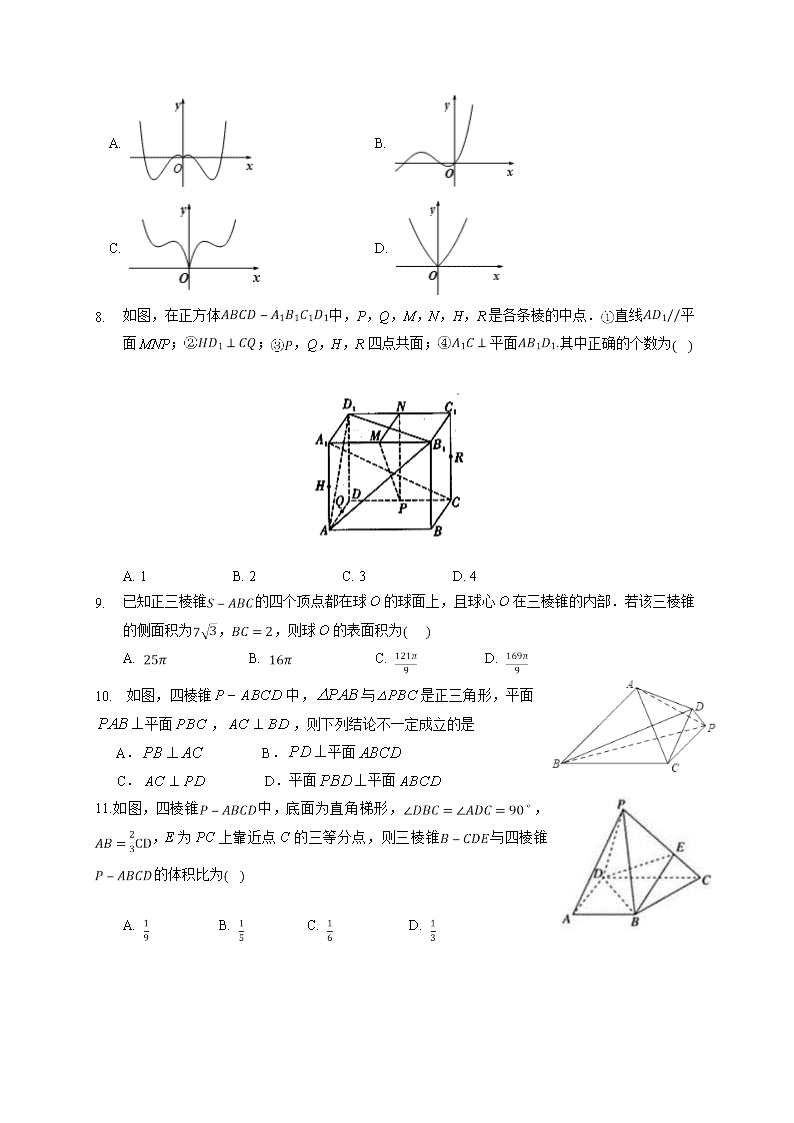‎ 1. 如图，在正方体中，P，Q，M，N，H，R是各条棱的中点．直线平面MNP；；，Q，H，R四点共面；平面其中正确的个数为    ‎ A. 1 B. 2 C. 3 D. 4‎ 2. 已知正三棱锥的四个顶点都在球O的球面上，且球心O在三棱锥的内部．若该三棱锥的侧面积为，，则球O的表面积为    ‎ A. B. C. D. ‎ ‎10. 如图，四棱锥中，与是正三角形，平面平面，，则下列结论不一定成立的是 A． B．平面 ‎ C． ‎ D．平面平面 ‎11.如图，四棱锥中，底面为直角梯形，，，E为PC上靠近点C的三等分点，则三棱锥与四棱锥的体积比为    ‎ A. B. C. D. ‎ ‎12.已知P为双曲线C：左支上一点，，分别为C的左、右焦点，M为虚轴的一个端点，若的最小值为，则C的离心率为 A. B. C. D. ‎ 二、 填空题（本大题共4小题，共20.0分）‎ ‎13.已知x，y取值如表：‎ x ‎0‎ ‎1‎ ‎3‎ ‎5‎ ‎6‎ y ‎1‎ m ‎3m 画散点图分析可知：y与x线性相关，且求得回归方程为，则__________．‎ ‎14.若一个圆台的母线长为l，上、下底面半径，满足，且圆台的侧面积为，则          ．‎ ‎15.甲乙两人练习射击，命中目标的概率分别为1/2和1/3，甲乙两人各射击一次，目标被命中的概率是__________．‎ ‎16.在平面上，我们如果用一条直线去截正方形的一个角，那么截下一个直角三角形，由勾股定理有：设想将正方形换成正方体，把截线换成截面．这时从正方体上截下一个角，那么截下一个三棱锥如果该三棱锥的三个侧面面积分别为1，2，4，则该三棱锥的底面EFG的面积是________．‎ 三、 解答题（本大题共6小题，共70.0分）‎ ‎17在直角坐标系xOy中，曲线的参数方程为：为参数，曲线：． Ⅰ在以O为极点，x轴的正半轴为极轴的极坐标系中，求，的极坐标方程； Ⅱ射线与的异于极点的交点为A，与的交点为B，求． ‎ ‎18.在直三棱柱中，，，D是AB的中点．‎ 求证：平面；‎ 若点P在线段上，且，求证：平面．‎ ‎19.BMI指数身体质量指数，英文为BodyMassIndex，简称是衡量人体胖瘦程度的一个标准，体重身高的平方．根据中国肥胖问题工作组标准，当时为肥胖．某地区随机调查了1200名35岁以上成人的身体健康状况，其中有200名高血压患者，被调查者的频率分布直方图如图：‎ Ⅰ求被调查者中肥胖人群的BMI平均值； Ⅱ填写下面列联表，并判断是否有的把握认为35岁以上成人患高血压与肥胖有关．‎ 肥胖 不肥胖 合计 高血压 非高血压 合计 k 附：，其中．‎ ‎ 20.四棱锥如图所示，其中四边形ABCD是直角梯形，，，平面ABCD，，AC与BD交于点G，COS，点M线段SA上． 若直线平面MBD，求的值； 若，求点A到平面SCD的距离．‎ ‎ ‎ ‎21.如图所示的几何体中，四边形是正方形，四边形是梯形，，且，平面平面ABC． Ⅰ求证：平面平面； Ⅱ若，，求几何体的体积． ‎ ‎ ‎ ‎22.已知函数，． 若，恒成立，求实数m的取值范围； 设函数，若在上有零点，求实数a的取值范围． ‎ 参考答案 一 选择题 1-12、ABBAB BDCDB BC 二 填空题 （13）3/2 （14）2 （15） （16）‎ 三解答题 ‎17.解：Ⅰ曲线为参数可化为普通方程：， 由可得曲线的极坐标方程为，曲线的极坐标方程为． Ⅱ射线与曲线的交点A的极径为， 射线与曲线的交点B的极径满足，解得， 所以．‎ ‎18.证明：连结，设交于点O，连结OD． 四边形是矩形是的中点．在中，OD分别是，AB的中点，              又平面，平面，平面； ，D是AB的中点， 又在直三棱柱中，底面侧面，交线为AB， 平面ABC，平面平面，． ， ，，又， ∽，从而，所以，．又，平面，平面 平面． ‎ ‎19.解：Ⅰ被调查者中肥胖人群的BMI平均值； ‎ Ⅱ高血压人群中肥胖的人数为：人，不肥胖的人数为：人， 非高血压人群中肥胖的人数为：，不肥胖的人数为：人，所以列联表如下：‎ 肥胖 不肥胖 合计 高血压 ‎70‎ ‎130‎ ‎200‎ 非高血压 ‎230‎ ‎770‎ ‎1000‎ 合计 ‎300‎ ‎900‎ ‎1200‎ 则K 的观测值：， 有的把握认为35岁以上成人患高血压与肥胖有关．‎ ‎20.【答案】解：连接MG． ，，且AB，CD在同一平面内，， 设，，得， 平面MBD，平面平面，平面SAC，， 故； 在平面SAD内作于点N 平面ABCD ， 又，，得平面SAD． 平面SAD，． 又，平面SCD． 角SCA的余弦值为， 即， 又，， 则，而，，求得，， 即点A到平面SCD的距离为． ‎ ‎21.证明：取BC的中点D，连接AD，D. 四边形是正方形，， 又平面平面ABC，平面平面． ‎ 平面ABC，平面ABC ．中，，，，又，平面． 四边形是梯形，，且．，四边形是平行四边形， ，又，，四边形是平行四边形． ，平面．又平面， 平面平面． Ⅱ解：由可得：三棱柱是直三棱柱，四边形是矩形，底面． 直三棱柱的体积， 四棱锥的体积． 几何体的体积． 22.解：由题意得的定义域为， ． ，、随x的变化情况如下表：‎ x ‎3‎ ‎0‎ 单调递减 极小值 单调递增 由表格可知：． 在上恒成立，． 函数在上有零点， 等价于方程在上有解． 化简，得． 设． 则， ，、随x的变化情况如下表：‎ x ‎1‎ ‎3‎ ‎0‎ ‎0‎ 单调递增 单调递减 单调递增 且，，， ． 作出在上的大致图象如图所示 当时， 在上有解． 故实数a的取值范围是． ‎