高考数学复习点拨-命题中的“大于(或小于)”的否定+算法初步+复习测试题 23页

高考数学复习点拨-命题中的 “大于(或小于)”的否定+算法初步+复习测试题 命题中的“大于(或小于)”的否定(附参考答案) 在简易逻辑中经常会碰到大于或小于的否定问题，而这类问题往往受思维的定势，容易 出差错。 以下是最近在国内一本很有影响的教学辅导书上的一个例题及其解答，现抄录如下： 例题：写出下列命题的逆命题、否命题和逆否命题，并判别其真假。 命题：“当 012 m 时，如果 012 3   m m ，那么 0652  mm ” 解：由 012 m 得： 2 1m ，又由 012 3   m m 得： 2 13  mm 或 ，结合 2 1m 得 2 1m ；由 0652  mm 得： 32  m 。由此可知，原命题可变为：“如果 2 1m ，那 么 32  m ”显然是真命题。 逆命题为“当 012 m 时，如果 0652  mm ，那么 012 3   m m ”，此命题即是“如 果 32  m ，那么 2 1 m ”，它是真命题。 否命题为“当 012 m 时，如果 012 3   m m ，那么 0652  mm ”，此命题即是“如 果 2 1 2 1  m ，那么 32  mm 或 ”，它是真命题 逆否命题为“当 012 m 时，如果 0652  mm ，那么 012 3   m m ”，此命题即是 “如果 32  mm 或 ，那么 2 1 2 1  m ”，它是真命题。 评注：上述解法在 012 3   m m 的否定上存在错误。 事实上， 012 3   m m  2 13  mm 或 ，结合大前提，结果为 2 1m ；而其否定不是由 012 3   m m 结合大前提所得的 2 1 2 1  m ，而是 2 1 2 1  m 或 2 1 m ，即 2 1 2 1  m 。从 而，否命题为““当 012 m 时，如果 012 3   m m 或 2 1m ，那么 0652  mm ”，此 命题即是“如果 2 1 2 1  m ，那么 32  mm 或 ”，它是真命题；逆否命题为“当 012 m 时，如果 0652  mm ，那么 012 3   m m 或 2 1 m ”，此命题即是“如果 32  mm 或 ， 那么 2 1 2 1  m ”，它是真命题。 如果将命题 p，非 p知识与集合 A，A 的补集 ACU 的知识联系起来学习，那么上面观 点容易理解。 结论：由上可见，“小于 0”的否定不一定是“大于等于 0”；“大于 0”的否定不一定是 “小于等于 0”。 一般地：（1）设  xf 、  xg 是两个整式函数，则命题 :p      00 xf xg 的 p 为      00 xf xg 或  xf =0 （2）设  xf 是整式函数，则命题  xfp : 0 的 p 为   0xf 或   0xf ，即 p 为   0xf 。 思考题：命题 P： 0 34 1 2   xx 的“非 P 形式”的复合命题是（ ） A． 0 34 1 2   xx ；B． 31  x ；C． 31  xx 或 ；D． 31  xx 或 。 解析：命题 P： 0 34 1 2   xx 的“非 P 形式”为 0 34 1 2   xx 或 0342  xx 即 0342  xx ，解得 31  xx 或 。故选 D。 高考数学复习参考题(附参考答案) 4、算法初步 一、选择题： 1．阅读如图所示的程序框图，运行相应的程序，输出的 n 的值为( )． A．1 B．2 C．3 D．4 【试题解析】第一次循环 1n ，判断 21 12  成立，则 211 n ；第二次循环，判断 22 22  不成立，则输出 2n .故选 B. 【选题意图】本题考查算法与程序框图，难度较小。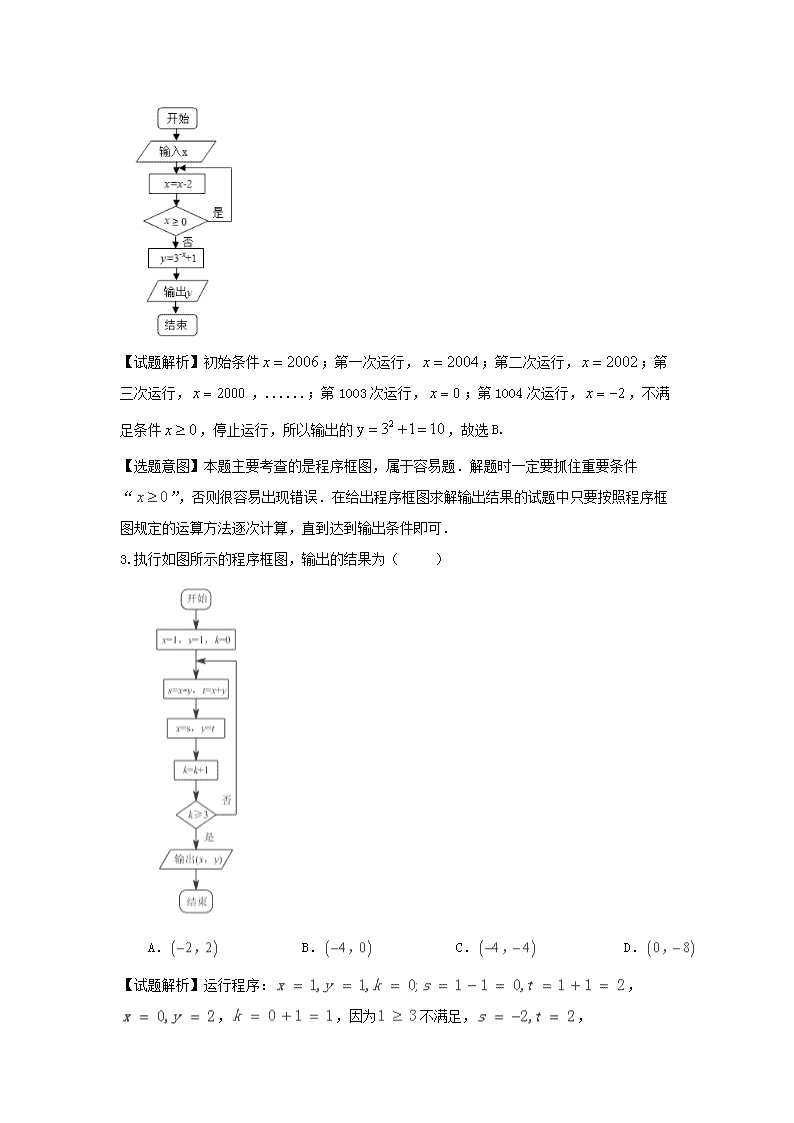 2.根据右边的图，当输入 x为2006时，输出的 y （ ） A．28 B．10 C．4 D．2 【试题解析】初始条件 2006x ；第一次运行， 2004x ；第二次运行， 2002x ；第 三次运行， 2000x ，......；第 1003 次运行， 0x ；第 1004 次运行， 2x ，不满 足条件 0x ，停止运行，所以输出的 1013y 2  ，故选 B. 【选题意图】本题主要考查的是程序框图，属于容易题．解题时一定要抓住重要条件 “ 0x  ”，否则很容易出现错误．在给出程序框图求解输出结果的试题中只要按照程序框 图规定的运算方法逐次计算，直到达到输出条件即可． 3.执行如图所示的程序框图，输出的结果为（ ） A．  2 2 ， B．  4 0 ， C．  4 4 ， D．  0 8， 【试题解析】运行程序： 1, 1, 0; 1 1 0, 1 1 2x y k s t         ， 0, 2x y  ， 0 1 1k    ，因为1 3 不满足， 2, 2s t   ， 2, 2, 2x y k    ，因为2 3 不满足， 4, 0s t   ， 4, 0, 3x y k    ，因为3 3 满足，输出( 4,0) . 【选题意图】本题考查程序框图的程序运行，本题为基础题，掌握循环程序的运行方法，框 图以赋值框和条件框为主，按照框图箭线方向和每个框的指令要求运行，注意条件框的要求 是否满足，运行程序时要准确. 4．执行下图的程序框图，若输入的 kba ,, 分别为 1，2，3，则输出的 M A． 3 20 B． 5 16 C． 2 7 D． 8 15 【试题解析】 由框图知其表示的算法执行过程如下： 初始化：输入 ;1;3,2,1  nkba 条件判断：是，进入循环. 循环第 1 次： ;2; 2 3,2, 2 3 2 11  nbaM 条件判断：是； 循环第 2 次： ;3; 3 8, 2 3, 3 8 3 22  nbaM 条件判断：是； 循环第 3 次： ;4; 8 15, 3 8, 8 15 8 3 2 3  nbaM 条件判断：否；退出循环. 输出 8 15 M ． 故选 D． 【选题意图】本题主要考查程序框图表示算法的意义及赋值语句，本题中的算法是一个循环 结构，循环体中依次对 abM ,, 进行循环赋值.处理本类题的关键是，按照程序框图，将每次 的循环赋值过程依次写出即可得出正确答案，注意赋值语句的特点，属于基础题． 5．执行如题(8)图所示的程序框图,如果输出 3s  ,那么判断框内应填入的条件是 （ ） A． 6k  B． 7k  C． 8k  D． 9k  开始 结束输入 a，b，k n =1 输出 M n =n＋1 b =M a =b M =a＋1 b n≤k 是 否 【试题分析】本题考查程序框图的识别和运行。第一次循环， 2log 3, 3s k  ，此时满足 条件,循环；第二次循环， 2 3log 3 log 4 2, 4s k    ，此时满足条件,循环；第三次循环， 2 3 4log 3 log 4 log 5, 5s k    ， 此 时 满 足 条 件 , 循 环 ； 第 四 次 循 环 ， 2 3 4 5log 3 log 4 log 5 log 6, 6s k     ， 此 时 满 足 条 件 , 循 环 ； 第 五 次 循 环 ， 2 3 4 5 6log 3 log 4 log 5 log 6 log 7, 7s k      ，此时满足条件,循环；第六次循环， 2 3 4 5 6 7log 3 log 4 log 5 log 6 log 7 log 8 3, 8s k        ，此时不满足条件，输出 3s  ， 所以判断框内应填入的条件是 7k  ，选 B. 【选题意图】本题考查了当型循环结构的程序框图和对数运算，根据框图的流程判断程序运 行的 S值是解题的关键。本题是嵌套的条件语句，要会灵活地把符号语言、图形语言、文字 语言进行相互转化． 6.执行如图所示的程序框图（算法流程图），输出的 n为（ ） （A）3 （B）4 （C）5 （D）6 【试题解析】 执行第一次循环体： ;2, 2 3  na 此时 ;005.0086.0414.15.1414.1 a 执行第二次循环体： ;3, 5 7  na 此时 ;005.0014.0414.14.1414.1 a 执行第三次循环体： ;4, 12 17  na 此时 005.0414.1 a ，此时不满足，判断条件，输 出 4n ,故选 B. 【选题意图】本题主要考查程序框图以及循环结构的判断.首先要明确循环的条件，其次在 计算的过程中要细心，本题还考查了考生的计算能力. 7． 执行右面的程序框图，如果输入的  3,1t ，则输出的 s属于 A．  4,3- B．  2,5- C．  3,4- D．  ,52- 【试题解析】由框图知其表示的算法是求分段函数       14 1,3 2 ttt tt s ， 在  3,1t 上的值域，当  1,1t 时，  3,3s ，当  3,1t 时，  4,3s ，所以  4,3s ， 故选 A． 【选题意图】本题主要考查程序框图表示算法的意义，本题 中的算法是一个条件结构，是基础题． 8．如果执行右边的程序框图，输入正整数  2NN 和实数 N21 ,..., aaa ，输出 A，B，则 A． BA 为 N21 ,..., aaa 的和 B． 2 BA 为 N21 ,..., aaa 的算术平均数 C． A和 B为 N21 ,..., aaa 中的最大数和最小数 开始 结束 输入 t s =3t 是 t＜1 否 s =4t－t 2 输出 S 开始 结束 k =1，A = a1，B = a1 输入 N，a1，a2，…，aN x = ak x＞A k≥N A = x B = x 是 是 否 x＜B 否 是 k = k＋1 输出 A，B 否 D． A和 B为 N21 ,..., aaa 中的最小数和最大数 【试题解析】由框图知其表示的算法是找 N个数中的最大值和最小值， A和 B分别为 N21 ,..., aaa 中的最大数和最小数，故选 C． 【选题意图】本题主要考查程序框图表示算法的意义，本题中的算法是一个复杂的算法，循 环结构嵌套了二重条件结构，是基础题． 9.根据右边框图，对于大于 2的整数 N ,输出的数列通项公式是 （ ） (A) 2n n  (B) 2( 1)n n   (C) 2nn  (D) 12nn  【试题解析】由已知程序框图依次可得 ,2,......,8,4,2 1321  nn aaaaa 故输出的数列 是首项和公比均为 2的等比数列，故有 n na 2 ，故选 C。 【选题意图】本题考查算法程序框图及推理能力，难度中等； 10.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行 该程序框图，若输入 ,a b分别为 14,18，则输出的 a ( ) A．0 B．2 C．4 D．14 【 试 题 解 析 】 程 序 在 执 行 过 程 中 ， ba, 的 值 依 次 为 ;2;2;6;10;4;18,14  baaabba 此时 2 ba ，程序结束，输出a的值为 2， 故选 B。 【选题意图】本题考查程序框图，要注意依序进行，认真判断条件来决定程序的执行方向， 属于中档题． 11．阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为( )． A．7 B．9 C．10 D．11 【试题解析】解析： , 3 1lg 3 1lg0,0,1  ssi 执行“否”： , 5 1lg 5 3lg 3 1lg0,3  si 执行“否”： ， 7 1lg 7 5lg 5 1lg,5  si 执行“否”： , 9 1lg 9 7lg 7 1lg,7  si 执行“否”： ,1 11 1lg 11 9lg 9 1lg,9  si 执行“是”：输出 9i .结束．故选 B. 【选题意图】本题考查程序框图，涉及对数运算，难度中等。 12. 下图是用模拟方法估计圆周率 的程序框图， P表示估计结果，则图中空白框内应填 入（ ） A. 1000 NP  B. 4 1000 NP  C. 1000 MP  D. 4 1000 MP  【试题解析】点 ( , )i ix y 落在单位圆内或圆上，随机产生 1000 个数，因此图中空白框内应填 入 4 1000 MP  ，故选 D。 【选题意图】本题考查程序框图，涉及几何概型，考查学生对知识的综合运用，难度较大。 二、填空题： 13.根据下列算法语句, 当输入 x 为 60 时, 输出 y 的值为______ 输入 x If x≤50 Then y=0.5 * x Else y=25+0.6*(x-50) End If 输出 y 【试题解析】 31)50(6.025,60  xyx ,所以答案是 31. 【选题意图】解决循环结构的框图问题，关键是理解并认清终止循环结构的条件及循环次 数．解决循环结构框图问题，首先要找出控制循环的变量其初值、步长、终值(或控制循环 的条件)，然后看循环体，循环次数比较少时，可依次列出即可获解，循环次数较多时可先 循环几次，找出规律，要特别注意最后输出的是什么，不要出现多一次或少一次循环的错误。 14.执行如图所示的程序框图，输出的 k的值为________ 否 【试题解析】初值为 0,3  ka ，进入循环体后， ;4, 16 3;3, 8 3;2, 4 3;1, 2 3  kakakaka 此时 4 1 a ，退出循环，故 4k ，答 案为 4. 【选题意图】本题主要考查的是程序框图，属于容易题．解题时一定要抓住重要条件 “ 1 4 a  ”，否则很容易出现错误．在给出程序框图求解输出结果的试题中只要按照程序框 图规定的运算方法逐次计算，直到达到输出条件即可． 15.执行右边的程序框图，输出的T 的值为 . 【试题解析】 初始条件 1, 1, 3n T n   成立方 ； 运行第一次： 1 0 1 31 1 , 2, 3 2 2 T xdx n n       成立； 运行第二次： 1 2 0 3 3 1 11, 3, 3 2 2 3 6 T x dx n n       不成立； 输出T 的值： 11. 6 结束。所以答案应填： 11. 6 【选题意图】本题考查了循环结构与定积分的计算，意在考查学生对程序框图的理解和基本 的计算能力，以程序框图为载体，可以展开对数列、函数、不等式、定积分等多种知识点的 考查，此题是一个范例.解题中要注意运算的准确性. 16.执行如图 2 所示的程序框图，如果输入 3n ，中输入的 S __________ 【试题解析】由题根据所给程序框图不难得到所求 S值即是求递推数列的连续前 3 项的和； 由题 1 1 1 3 1 3 3 5 5 7 7       ，故为 3 7 . 【选题意图】识别运行算法流程图和完善流程图是高考的热点．解答这一类问题，第一，要 明确流程图的顺序结构、条件结构和循环结构；第二，要识别运行流程图，理解框图所解决 的实际问题；第三，按照题目的要求完成解答．对流程图的考查常与数列和函数等知识相结 合，进一步强化框图问题的实际背景． 高考数学复习测试题一(附参考答案) 姓名 得分 一.选择题. 1. 设 全 集 U = R ， A = 1 0x x       ， 则 UA= （ ）． A． 1 0x x       B.｛x | x > 0｝ C.｛x | x≥0｝ D. 1x x    ≥0    2. 在 数 列 1 ， 2 ， 2 ， 3 ， 3 ， 3 ， 4 ， 4 ， 4 ， 4 ， …… 中 ， 第 25 项 为 （ ）． A．25 B．6 C．7 D．8 3. 曲线 ) 4 cos() 4 sin(2   xxy 和直线 2 1 y 在 y 轴右侧的交点按横坐标从小到大依 次 记 为 P1 ， P2 ， P3 ， … ， 则 |P2P4| 等 于 （ ）． A． B．2 C．3 D．4 4．右图为函数 logny m x  的图象，其中 m，n 为常数，（ ） 则下列结论正确的是 A．m < 0 , n >1 B．m > 0 , n > 1 C．m > 0 , 0 < n <1 D． m < 0 , 0 < n < 1 5.若 x、y 满足不等式组 x + y≥0 x 2 + y 2≤1 ，则 2x + y 的取值范围是 (A) [ 2 2 , 5 ] (B) [－ 2 2 , 2 2 ] (C) [－ 2 2 , 5 ] (D) [－ 5 , 5 ] 6. 直线 03  yx 绕原点按顺时针方向旋转 30°所得直线与圆 3)2( 22  yx 的位置 关系是 （ ） A．直线与圆相切 B．直线与圆相交但不过圆心 C．直线与圆相离 D．直线过圆心 7. 已知椭圆 2 2 2 2 1( 0) 2 2 x y a b a b + = > > 与双曲线 2 2 2 2 1x y a b - = 有相同的焦点，则椭圆的离心率为 A． 2 2 B． 1 2 C． 6 6 D． 2 6 6 （ ） 8.三位同学在研究函数 f (x) = x 1 + | x | (x∈R) 时，分别给出下面三个结论： ① 函数 f (x) 的值域为 (－1,1) ② 若 x1≠x2，则一定有 f (x1)≠f (x2) ③ 若规定 f1(x) = f (x)，fn+1(x) = f [ fn(x)]，则 fn(x) = x 1 + n | x | 对任意 n∈N* 恒成立. 你 认 为 上 述 三 个 结 论 中 正 确 的 个 数 有 （ ） (A) 0 个 (B) 1 个 (C) 2 个 (D) 3 个 二.填空题. 9. 若双曲线的渐近线方程为 xy 3 ，它的一个焦点是  0,10 ，则双曲线的方程是 __________； 10. 已知函数 ) 12 (), 4 (cos) 4 (cos)( 22  fxxxf 则 等于 ； 11. 在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是 1 颗珠宝, 第二件首饰是 由 6颗珠宝构成如图 1所示的正六边形, 第三件首饰是由 15颗珠宝构成如图 2所示的正 六边形, 第四件首饰是由 28颗珠宝构成如图 3所示的正六边形, 第五件首饰是由 45颗珠 宝构成如图 4所示的正六边形, 以后每件首饰都在前一件上 ,按照这种规律增加一 定 数 量 的 珠 宝 ,使 它 构 成 更 大 的 正 六 边形 , 依 此 推 断 第 6 件 首饰上应有 _______________ 颗 珠 宝 ; 则 前 n 件 首 饰 所 用 珠 宝 总 数 为 __________________________颗.(结果用 n表示) 12. 若函 数 )2,2()( 2 1)(     在为常数 ，a x axxf 内为 增函 数， 则实数 a 的取 值范 图 1 图 2 图 3 图 4 围 ； 以下为选做题,请从中任选两题. 13.已知圆的直径 AB=10cm，C 是圆周上一点（不同于 A、B 点），CD AB 于 D，CD=3cm， 则 BD=_______________。 14.已知 为参数，则点(3，2)到方程 　        siny cosx 的距离的最大值是_____________。 15.已知 x、yR  ，且 4x+3y=1，则 x 1 ＋ y 1 的最小值为______________。 三.解答题. 16.(12)已知函数   )sin(   xxf ( 0 ，  0 )为偶函数，且其图像上相邻的一个最 高点和最低点之间距离为 24  . ⑴求  xf 的解析式； ⑵若 5cottan   ，求   tan1 1) 4 2(2  f 的值。 17.(12) 已知 )(xf 是定义在 R 上的函数，对于任意的实数 a，b，都有 ，)()()( abfbafabf  1)2( f且 。 （Ⅰ）求 ) 2 1(f 的值； （Ⅱ）令 ),2( n n fb  求证： 为}2{ n nb 等差数列． 18. (14)某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、 获得利润及每天资源限额（最大供应量）如下表所示： 产品 消耗量 资源 甲产品 （每吨） 乙产品 （每吨） 资源限额 （每天） 煤（t） 9 4 360 F O A P Q y x 电力（kw·h） 4 5 200 劳力（个） 3 10 300 利润（万元） 6 12 问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？ 19. （本小题满分 14 分） 设椭圆 C： )0(12 2 2 2  ba b y a x 的左焦点为 F，上顶点为 A，过点 A与 AF 垂直的直 线分别交椭圆 C与 x轴正半轴于点 P、Q，且 8AP= PQ 5   . ⑴求椭圆 C 的离心率； ⑵若过 A、Q、F 三点的圆恰好与直线 l： 3 3 0x y   相切，求椭圆 C 的方程. 20. （本小题满分 14 分） 已 知 2)1x()x(f  ， )1x(10)x(g  ， 数 列  na 满 足 2a1  ， 0)a(f)a(g)aa( nnn1n  ， 1)a)(2n( 10 9b nn  ． （Ⅰ）求证：数列 1a n  是等比数列； （Ⅱ）当 n 取何值时， nb 取最大值，并求出最大值； （III）若 1m 1m m m b t b t    对任意 *Nm 恒成立，求实数 t的取值范围． 21. （本小题满分 14 分） 已知 ( ) ( )( )f x x x a x b   ，点 A(s,f(s)), B(t,f(t)) (I) 若 1a b  ,求函数 ( )f x 的单调递增区间； (II)若函数 ( )f x 的导函数 ( )f x 满足：当|x|≤1 时，有| ( )f x |≤ 2 3 恒成立，求函数 ( )f x 的解析表达式； (III)若 07 时， 1 b b n 1n  ， n1n bb  ． ∴当 n=7 或 n=8 时， nb 取最大值，最大值为 7 8 87 10 9bb  ．……8 分 （III）由 1m 1m m m b t b t    ，得 0] )3m(9 10t 2m 1[t m     （*） 依题意（*）式对任意 *Nm 恒成立， ①当 t=0 时，（*）式显然不成立，因此 t=0 不合题意．…………9 分 ②当 t<0 时，由 0 )3m(9 10t 2m 1     ，可知 0t m  （ *Nm ）． 而当 m 是偶数时 0t m  ，因此 t<0 不合题意．…………10 分 ③当 t>0 时，由 0t m  （ *Nm ）, ∴ 0 )3m(9 10t 2m 1     ∴ )2m(10 )3m(9t    ． （ *Nm ）……11 分 设 )2m(10 )3m(9)m(h    （ *Nm ） ∵ )2m(10 )3m(9 )3m(10 )4m(9)m(h)1m(h       = 0 )3m)(2m( 1 10 9    , ∴   )m(h)1m(h)2(h)1(h ． ∴ m)(h 的最大值为 5 6)1(h  ．所以实数 t 的取值范围是 5 6t  ．………13 分 21.解：(I) f (x)=x3 -2x2 +x, f  (x)=3x2 -4x+1, 因为 f(x)单调递增， 所以 f  (x)≥0， 即 3x2-4x+1≥0, 解得，x≥1, 或 x≤ 3 1 ,……………………………2 分 故 f(x)的增区间是(-∞， 3 1 )和[1,+ ∞]. …………………………3分 (II) f  (x)=3x2 -2(a+b)x+ab. 当 x∈[-1，1]时，恒有| f  (x)|≤ 2 3 .………………………4 分 故有 2 3  ≤ f  (1)≤ 2 3 ， 2 3  ≤ f  (-1)≤ 2 3 ， 2 3  ≤ f  (0)≤ 2 3 ,………………………5 即            �. 2 3 ≤ab ≤ 2 3 �, 2 3 ≤ ab)ba(23 ≤ 2 3 �, 2 3 ≤ ab)ba(23 ≤ 2 3 ………6 ①+②，得 2 9  ≤ab≤ 2 3  ， 又由③，得 ab= 2 3  ， 将上式代回①和②，得 a+b=0,故 f(x)=x3 2 3  x. ……………………9分 (III) 假设OA⊥OB , 即OA OB = ))(,())(,( tftsfs  = st+f(s)f(t)=0, ……………10 分 (s-a)(s-b)(t-a)(t-b)=-1, [st-(s+t)a+a2][st-(s+t)b+b2]=-1, ……………………………………11 分 由 s，t 为 f  (x)=0 的两根可得， s+t= 3 2 (a+b), st= 3 1 , (0