高中数学选修2-1公开课课件2_2_1椭圆及其标准方程(第1课时)(版本一) 20页

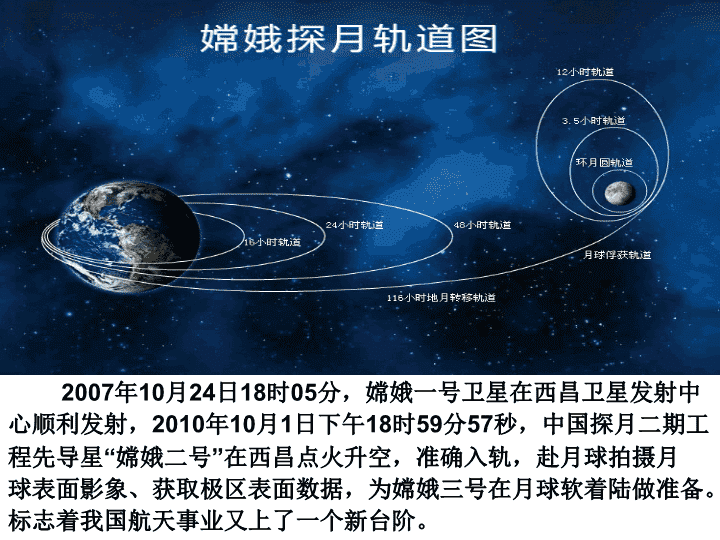
2.1.1 椭圆的定义与标准方程 —— 仙女座星系 星系中的椭圆 2007 年 10 月 24 日 18 时 05 分，嫦娥一号卫星在西昌卫星发射中心顺利发射， 2010 年 10 月 1 日下午 18 时 59 分 57 秒，中国探月二期工程先导星“嫦娥二号”在西昌点火升空，准确入轨，赴月球拍摄月球表面影象、获取极区表面数据，为嫦娥三号在月球软着陆做准备。标志着我国航天事业又上了一个新台阶。 如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢？ 生活中的椭圆 一、合作探究，形成概念： 1. 取一条定长的细绳，把它的两端都固定在图板的同一点处，套上铅笔，拉紧绳子，移动笔尖，这时笔尖（动点）画出的轨迹是一个什么图形？笔尖（动点）满足什么几何条件？ 2. 如果把细绳的两端拉开一段距离，分别固定在图板的两点处，套上铅笔，拉紧绳子，移动笔尖，画出的又是什么图形？这一过程中，笔尖（动点）满足什么几何条件？ 我们把平面内到两个定点 F 1 ， F 2 的距离之和等于 常数 的点的轨迹叫做椭圆。这两个定点叫做椭圆的 焦点 ， 两焦点的距离叫做 焦距。 椭圆的定义 : （大于 | F 1 F 2 | ） 请同学们根据上面作图过程，总结椭圆的定义。 结论： 若常数 大于 |F 1 F 2 |, 则点 M 的轨迹是（ ） 若常数 等于 |F 1 F 2 | ，则点 M 的轨迹是（ ） 若常数 小于 |F 1 F 2 | ，则点 M 的轨迹（ ） 思考 : 当点 M 到 F 1 、 F 2 的距离之和不大于 | F 1 F 2 | 时，点 M 的轨迹是什么？ 椭圆 线段 F 1 F 2 不存在 椭圆的定义：（与圆 类比 ） 圆： O P 椭圆 平面内 与 一个 定点 的 距离等于常数 （ 大于 0 ）的点的轨迹叫作圆，这个定点叫做圆的 圆心 ，定长叫做圆的 半径 圆的定义： 平面内 与两个定点 　　 的 距离和 等于常数 （ 大于 　　 ） 的点的轨迹叫作椭圆 ， 这两个定点叫做椭圆的 焦点 ，两焦点间的距离叫做椭圆的 焦距 ． 2 1 F F 椭圆的定义： 椭圆的方程的推导 独立思考轨迹方程的一般步骤，并按其方法及提示独立逐步求椭圆的一般方程。 建 设 现（限） 以经过椭圆焦点 F 1 ， F 2 的直线为 x 轴，线段 F 1 F 2 的中垂线为 y 轴，建立直角坐标系 xoy 。 设 M （ x ， y ） 是椭圆上任一点， 设椭圆的焦距为 2c ，点 M 与两焦点的距离之和为常数 2a 。 故椭圆的两焦点坐标分别为 F 1 (-c,0) 和 F 2 (c,0) 由椭圆的定义得 （ a > c ） 2 a 代 化 两边同时除以 ，得 移项，得 平方化简，得 再平方化简，得 椭圆方程的建立 —— 步骤一： 建 立直角坐标系 步骤二： 设 动点坐标 步骤四： 代 入坐标 步骤五： 化 简方程 步骤三： 限 制条件，列等式 则方程可化为 观察左图， 你们能从中找出表示 c 、 a 的线段吗？ a 2 -c 2 有什么几何意义？ 由两点间的距离公式，可知： 设 |F 1 F 2 |=2c(c ＞ 0) ， M(x ， y) 为椭圆上任意一点，则有 F 1 (0,-c) ， F 2 (0,c) ， 又由椭圆 的定义可得： |MF 1 |+ |MF 2 |=2a （请大家比较一下上面两式的不同，独立思考后回答椭圆的标准方程。） 焦点在 Y 轴 焦点在 X 轴 焦点在 x 轴上的标准方程： 焦点在 y 轴上的标准方程： 如果已知椭圆的标准方程，如何确定焦点在哪条坐标轴上？ 思考？ （ 1 ）焦点在 x 轴的椭圆， x 2 项分母较大 . （ 2 ）焦点在 y 轴的椭圆， y 2 项分母较大 . X 型 y 型 标准方程中，分母哪个大，焦点就在哪个轴上 ! 标 准 方 程 相 同 点 焦点位置的判断 不 同 点 图 形 焦 点 坐 标 a 、 b 、 c 的关系 焦点在 x 轴上 焦点在 y 轴上 y x M O F 1 F 2 练习： 下列方程哪些表示椭圆？若表示椭圆焦点在那个轴上？（ 独立思考后回答 ） 例 1 、填空：（独立思考后回答） (1) 已知椭圆的方程为： , 则 a=_____ ， b=_______ ， c=_______ ， 焦点坐标为： ，焦距 等于 _____; 若曲线上一点 P 到焦点 F 1 的距离为 3 ，则 点 P 到另一个焦点 F 2 的距离等于 _________ ， 则 ∆ F 1 PF 2 的周长为 ___________ 2 1 (0,-1) 、 (0,1) 2 |PF 1 |+|PF 2 |=2a 三、迁移应用，能力提高 判断椭圆标准方程的焦点在哪个轴上的准则： 焦点在分母大的那个轴上。 F 1 F 2 ( 2) 已知椭圆的方程为： ，则 a=_____ ， b=_______ ， c=_______ ，焦点坐标为： ____________ 焦距等于 ______; 若 CD 为过左焦点 F 1 的弦，则 ∆ F 2 CD 的周长为 ________ 5 4 3 (3,0) 、 (-3,0) 6 ２ 0 F 1 F 2 C D 判断椭圆标准方程的焦点在哪个轴上的准则： 焦点在分母大的那个轴上。 |CF 1 |+|CF 2 |=2a （ 3 ） a= 5 ， c= 4 的椭圆标准方程是 。 或 课堂小结： 1 、椭圆的定义：我们把平面内与两个定点 的距离之和等于 常数 的点的轨迹叫做椭圆。 （大于 ） （ a > c ） 即 2 a 2 、椭圆的图形与标准方程 这两个定点 F 1 ,F 2 叫做椭圆的焦点，两焦点间的距离 |F 1 F 2 | 叫做焦距。 标准方程中，分母哪个大，焦点就在哪个轴上 ! 标 准 方 程 相 同 点 焦点位置的判断 不 同 点 图 形 焦 点 坐 标 a 、 b 、 c 的关系 焦点在 x 轴上 焦点在 y 轴上 y x M O F 1 F 2 作业布置