高考数学【文科】真题分类详细解析版专题3 函数（解析版） 71页

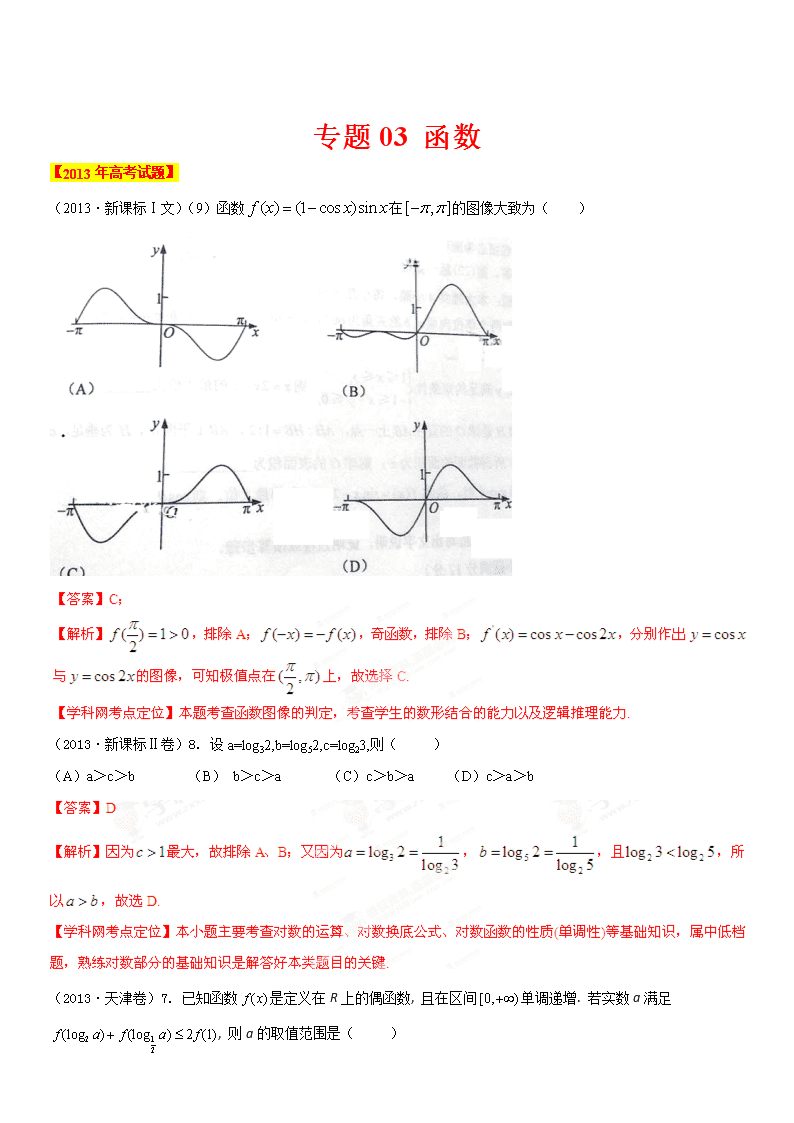
专题03 函数 ‎【2013年高考试题】‎ ‎（2013·新课标Ⅰ文）（9）函数在的图像大致为（ ）‎ ‎（2013·新课标Ⅱ卷）8. 设a=log32,b=log52,c=log23,则（ ）‎ ‎（A）a＞c＞b （B） b＞c＞a （C）c＞b＞a （D）c＞a＞b ‎（2013·天津卷）7. 已知函数是定义在R上的偶函数, 且在区间单调递增. 若实数a满足, 则a的取值范围是（ ）‎ ‎ (A) (B) ‎ ‎ (C) (D) ‎ ‎（2013·天津卷）8. 设函数. 若实数a, b满足, 则（ ）‎ ‎ (A) (B) ‎ ‎ (C) (D) ‎ ‎（2013·陕西文）3. 设a, b, c均为不等于1的正实数, 则下列等式中恒成立的是 ‎ (A) (B) ‎ ‎ (C) (D) ‎ ‎【答案】D ‎（2013·山东文）5. 函数的定义域为 A. B. C. D. ‎ ‎（2013·山东文）3. 已知函数为奇函数,且当时, ,则 ‎ A. B. C. D. ‎ ‎（2013·辽宁文）（12）已知函数设表示中的较大值，表示中的较小值，记得最小值为得最小值为,则 ‎（A） （B） ‎ ‎（C） （D）‎ ‎（2013·辽宁文）（7）已知函数 A． B． C． D． ‎ ‎（2013·湖南文）6.函数f（x）=㏑x的图像与函数g（x）=x2-4x+4的图像的交点个数为（ ）‎ A.0 B‎.1 C.2 D.3‎ ‎（2013·湖南文）4.已知f（x）是奇函数，g（x）是偶函数，且f（－1）+g（1）=2，f（1）+g（－1）=4，则g（1）等于（ ）‎ A.4 B‎.3 C.2 D.1‎ ‎（2013·广东文） 2．函数的定义域是 A． B． C． D．‎ ‎（2013·福建文）13.已知函数________ ‎ ‎（2013·福建文）12．设函数一定正确的是（ ）‎ A． B． ‎ C． D．‎ ‎（2013·福建文）7．若（ ）‎ A． B． C． D．‎ ‎（2013·大纲文）13. 设是以2为周期的函数，且当时， .‎ ‎【答案】-1‎ ‎【解析】∵是以2为周期的函数，且时，，‎ 则.‎ ‎【学科网考点定位】函数求值 ‎（2013·大纲文）6.函数的反函数（ ）‎ ‎（A） （B） （C） （D）‎ ‎（2013·新课标Ⅱ卷）16. 函数的图像向右平移个单位后，与函数的图像重合，则=___________.‎ ‎（2013·北京文）（13）函数的值域为_________.‎ ‎（2013·北京文）（3）下列函数中，既是偶函数又在区间上单调递减的是（ ）‎ ‎（A） (B) （C） (D) ‎ ‎（2013·浙江文）7、已知，函数f(x)=ax2+bx+c.若，则（ ）‎ A、 B、 ‎ C、 D、‎ ‎（2013·安徽文）（(8) 函数的图像如图所示，在区间上可找到个不同的数，使得，则的取值范围为 ‎ (A) (B) ‎ ‎ (C) (D) ‎ ‎（2013·安徽文）（10）已知函数有两个极值点，若，则关于的方程的不同实根个数为 ‎（A）3 (B) 4‎ ‎(C) 5 (D) 6‎ ‎（2013·安徽文）（（11） 函数的定义域为_____________.‎ ‎（2013·安徽文）（10）已知函数有两个极值点，若，则关于的方程的不同实根个数为 ‎（A）3 (B) 4‎ ‎(C) 5 (D) 6‎ ‎（2013·江西文）21.（本小题满分14分）‎ 设函数.为常数且 ‎（1）当时，求；‎ ‎（2）若满足，但，则称为的二阶周期点.证明函数有且仅有两个二阶周期点，并求二阶周期点；‎ ‎（3）对于（2）中的，设，记的面积为，求 在区间上的最大值和最小值。‎ ‎（2013·上海文）20．（本题满分14分）本题共有2个小题．第1小题满分6分，第2小题满分8分．‎ 甲厂以千米/小时的速度匀速生产某种产品（生产条件要求），每小时可获得的利润是元．‎ ‎（1）求证：生产千克该产品所获得的利润为；‎ ‎（2）要使生产千克该产品获得的利润最大，问：甲厂应该如何选取何种生产速度？并求此最大利润．‎ ‎【学科网考点定位】考查函数的性质及实际应用，属中档题。‎ ‎（2013·新课标Ⅱ卷）（21）(本小题满分12分)‎ 己知函数.‎ ‎(I)求f(x)的极小值和极大值；‎ ‎(II)当曲线y = f(x)的切线的斜率为负数时，求在x轴上截距的取值范围.‎ ‎【2012年高考试题】‎ ‎1.【2012高考安徽文3】（）·（4）=‎ ‎（A） （B） （C）2 （D）4‎ ‎【答案】D ‎【解析】。‎ ‎2.【2012高考新课标文11】当00，y>0，函数f(x)满足f（x＋y）＝f（x）f（y）”的是 ‎ ‎（A）幂函数 （B）对数函数 （C）指数函数 （D）余弦函数 答案：C 解析：本题考查幂的运算性质 ‎ ‎4.（2010辽宁文数）（12）已知点在曲线上，为曲线在点处的切线的倾斜角，则的取值范围是 ‎(A)[0,) (B) （C） (D) ‎ 答案： D 解析：.，，‎ 即，‎ ‎5.（2010辽宁文数）（10）设，且，则 ‎（A） （B）10 （C）20 （D）100‎ 答案：A 解析：选A.又 ‎6.（2010辽宁文数）（4）已知，函数，若满足关于的方程，则下列选项的命题中为假命题的是 ‎（A） （B） ‎ ‎（C） （D）‎ ‎7.（2010全国卷2文数）（7）若曲线在点处的切线方程是，则 ‎（A） (B) ‎ ‎(C) (D) ‎ ‎8.（2010全国卷2文数）（4）函数y=1+ln(x-1)(x>1)的反函数是 ‎（A）y=-1(x>0) (B) y=+1(x>0) ‎ ‎(C) y=-1(x R) (D）y=+1 (x R)‎ ‎9.（2010安徽文数）（7）设，则a，b，c的大小关系是 ‎（A）a＞c＞b （B）a＞b＞c （C）c＞a＞b （D）b＞c＞a 答案：A 解析:在时是增函数，所以，在时是减函数，所以。‎ ‎10.（2010安徽文数）（6）设,二次函数的图像可能是 ‎11.（2010重庆文数）（4）函数的值域是 ‎（A） （B）‎ ‎（C） （D）‎ ‎12.（2010浙江文数）（9）已知x是函数f(x)=2x+ 的一个零点.若∈（1，），‎ ‎∈（，+），则 ‎（A）f()＜0，f()＜0 （B）f()＜0，f()＞0‎ ‎（C）f()＞0，f()＜0 （D）f()＞0，f()＞0‎ 答案：B 解析：考察了数形结合的思想，以及函数零点的概念和零点的判断，属中档题 ‎13.（2010浙江文数）2.已知函数 若 =‎ ‎(A)0 (B)1 (C)2 (D)3‎ 答案：B 解析：+1=2，故=1 ‎ ‎14.（2010天津文数）（10）设函数，则的值域是 ‎（A） （B） （C）（D）‎ ‎15.（2010天津文数）‎ ‎(6)设 ‎(A)a0. ‎ ‎（Ⅰ）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；‎ ‎（Ⅱ）若在区间上，f（x）>0恒成立，求a的取值范围.‎ ‎（Ⅱ）解：f’(x)=.令f’(x)=0，解得x=0或x=.‎ 以下分两种情况讨论：‎ ‎【2009高考试题】‎ ‎1．( 2009·福建文2)． 下列函数中，与函数 有相同定义域的是 ‎ A ． B． C． D．‎ 答案：A 解析：解析 由可得定义域是的定义域；的定义域是≠0；‎ 的定义域是定义域是。故选A．‎ ‎2．( 2009·福建文8)．定义在R上的偶函数的部分图像如右图所示，则在上，下列函数中与的单调性不同的是 A．‎ B． ‎ C． ‎ D．‎ ‎3．( 2009·福建文11)．若函数的零点与的零点之差的绝对值不超过0．25， 则可以是 A． B． ‎ C． D． ‎ ‎4． (2009·广东文4) 若函数是函数的反函数，且，则 ‎ A． B． C． D．2 ‎ ‎5．( 2009·辽宁文6)已知函数满足：x≥4,则＝；当x＜4时＝，则＝‎ ‎（A） （B） （C） （D）‎ 答案：A 解析：∵3＜2＋log23＜4,所以f(2＋log23)＝f(3＋log23) 且3＋log23＞4‎ ‎ ∴＝f(3＋log23)‎ ‎ ＝‎ ‎6． (2009·辽宁文理9)已知偶函数在区间上单调增加，则的x取值范围是 ‎ ‎ 答案： A ‎ 解析：由已知有，即，‎ ‎∴。‎ ‎7．( 2009·山东文理6．) x ‎ y ‎ ‎1 ‎ ‎1 ‎ D ‎ O ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ C ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ B ‎ ‎1 ‎ x ‎ y ‎ ‎1 ‎ O ‎ A ‎ 函数的图像大致为( )．‎ ‎8．( 2009·山东文7)定义在R上的函数f(x)满足f(x)= ，则 f（3）的值为( )‎ A．-1 B． ‎-2 C．1 D． 2‎ ‎ ‎ ‎9．( 2009·山东文10)定义在R上的函数f(x)满足f(x)= ，则f（2009）的值为( )‎ A．-1 B． ‎0 C．1 D． 2‎ ‎10．( 2009·山东文12．)12． 已知定义在R上的奇函数，满足,且在区间[0,2]上是增函数,则( )． ‎ A． B． ‎ C． D． ‎ ‎,即,故选D． ‎ 答案：D．‎ ‎11．( 2009·天津文15) 5．设，则 A a0)的单调递增区间是 ．‎ 解析：由可得,答案:.‎ ‎8.(辽宁文15)若函数在处取极值，则 ‎ 解析：f’(x)＝‎ ‎ f’(1)＝＝‎0 Þ a＝3‎ 答案：3‎ ‎9.(宁夏海南文13)曲线在点（0,1）处的切线方程为 。‎ 解法2 （分离变量法）上述也可等价于方程在内有解，显然可得 ‎11．（2008·广东文17）（本小题满分12分）‎ 某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层‎2000平方米的楼房。经测算，如果将楼房建为x(x≥10)层，则每平方米的平均建筑费用为560+48x ‎（单位：元）。为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？‎ ‎（注：平均综合费用＝平均建筑费用+平均购地费用，平均购地费用＝）‎ ‎12．(2008·山东文21)（本小题满分12分）‎ 设函数，已知和为的极值点．‎ ‎（Ⅰ）求和的值；‎ ‎（Ⅱ）讨论的单调性；‎ ‎（Ⅲ）设，试比较与的大小．‎