高中数学 1-1-3 导数的几何意义双基限时训练 新人教版选修2-2 4页

‎【名师一号】2014-2015学年高中数学 ‎1-1-3‎ 导数的几何意义双基限时训练 新人教版选修2-2‎ ‎1．设f′(x0)＝0，则曲线y＝f(x)在点(x0，f(x0))处的切线(　　)‎ A．不存在　　　　　　　 B．与x轴垂直 C．与x轴平行 D．与x轴平行或重合 答案　D ‎2．一木块沿某一斜面自由下滑，测得下滑的水平距离s与时间t之间的函数关系为s＝t2，则当t＝2时，此木块在水平方向的瞬时速度为(　　)‎ A. 2 B. 1‎ C. D. 解析　s′＝ ＝ ‎＝ ＝ (t＋Δt)＝t.‎ ‎∴当t＝2时，s′＝.‎ 答案　C ‎3．若曲线y＝h(x)在点P(a，h(a))处切线方程为2x＋y＋1＝0，则(　　)‎ A．h′(a)<0 B．h′(a)>0‎ C．h′(a)＝0 D．h′(a)的符号不定 解析　由2x＋y＋1＝0，得h′(a)＝－2<0.‎ ‎∴h′(a)<0.‎ 答案　A ‎4．曲线y＝在点(3,3)处的切线方程的倾斜角α等于(　　)‎ A．45° B．60°‎ C．135° D．120°‎ 解析　k＝y′＝ ＝ ‎＝ ＝－.‎ ‎∴当x＝3时，tanα＝－1.∴α＝135°.‎ 答案　C ‎5．在曲线y＝x2上切线倾斜角为的点是(　　)‎ A．(0,0) B．(2,4)‎ C．(，) D．(，)‎ 解析　y′＝ ＝ ‎＝ ＝ (2x＋Δx)＝2x.‎ 令2x＝tan＝1，∴x＝，y＝.‎ 故所求的点是(，)．‎ 答案　D ‎6．已知曲线y＝2x2上一点A(2,8)，则过点A的切线的斜率为________．‎ 解析　k＝f′(2)＝ ‎＝ ＝ (8＋2Δx)＝8.‎ 答案　8‎ ‎7．若函数f(x)在x0处的切线的斜率为k，则极限 ＝________.‎ 解析　 ‎＝－ ＝－k.‎ 答案　－k ‎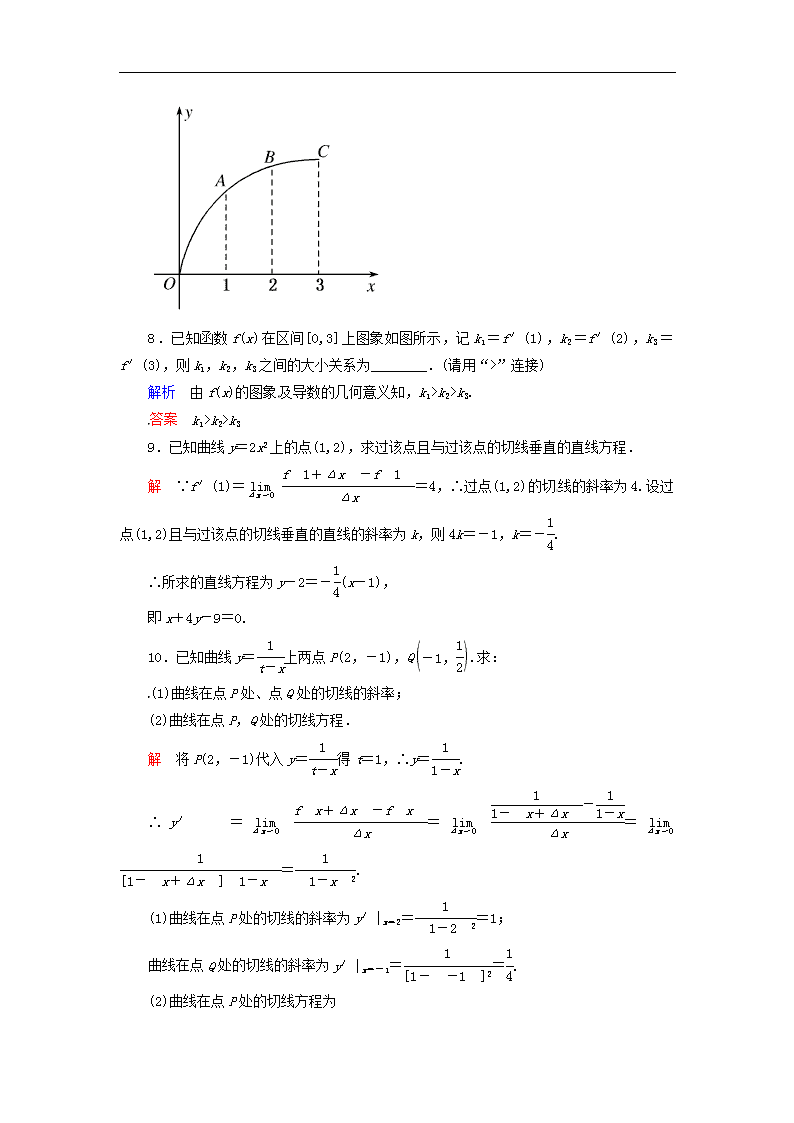8．已知函数f(x)在区间[0,3]上图象如图所示，记k1＝f′(1)，k2＝f′(2)，k3＝f′(3)，则k1，k2，k3之间的大小关系为________．(请用“>”连接)‎ 解析　由f(x)的图象及导数的几何意义知，k1>k2>k3.‎ 答案　k1>k2>k3‎ ‎9．已知曲线y＝2x2上的点(1,2)，求过该点且与过该点的切线垂直的直线方程．‎ 解　∵f′(1)＝ ＝4，∴过点(1,2)的切线的斜率为4.设过点(1,2)且与过该点的切线垂直的直线的斜率为k，则4k＝－1，k＝－.‎ ‎∴所求的直线方程为y－2＝－(x－1)，‎ 即x＋4y－9＝0.‎ ‎10．已知曲线y＝上两点P(2，－1)，Q.求：‎ ‎(1)曲线在点P处、点Q处的切线的斜率；‎ ‎(2)曲线在点P，Q处的切线方程．‎ 解　将P(2，－1)代入y＝得t＝1，∴y＝.‎ ‎∴y′＝ ＝ ＝ ＝.‎ ‎(1)曲线在点P处的切线的斜率为y′|x＝2＝＝1；‎ 曲线在点Q处的切线的斜率为y′|x＝－1＝＝.‎ ‎(2)曲线在点P处的切线方程为 y－(－1)＝x－2，即x－y－3＝0.‎ 曲线在点Q处的切线方程为 y－＝(x＋1)，即x－4y＋3＝0.‎ ‎11．已知点M(0，－1)，F(0,1)，过点M的直线l与曲线y＝x3－4x＋4在x＝2处的切线平行．‎ ‎(1)求直线l的方程；‎ ‎(2)求以点F为焦点，l为准线的抛物线C的方程．‎ 解　(1)∵f′(2)＝‎ ＝0，‎ ‎∴直线l的斜率为0，其直线方程为y＝－1.‎ ‎(2)∵抛物线以点F(0,1)为焦点，y＝－1为准线，∴设抛物线的方程为x2＝2py，则－＝－1，p＝2.故抛物线C的方程为x2＝4y.‎ ‎12．已知曲线y＝x2＋1，问是否存在实数a，使得经过点(1，a)能作出该曲线的两条切线？若存在，求出实数a的取值范围；若不存在，请说明理由．‎ 解　存在．‎ 理由如下：‎ ‎∵y＝x2＋1，‎ ‎∴y′＝ ＝ ＝‎ ＝2x.‎ 设切点坐标为(t，t2＋1)，‎ ‎∵y′＝2x，∴切线的斜率为k＝y′|x＝t＝2t.‎ 于是可得切线方程为y－(t2＋1)＝2t(x－t)．‎ 将(1，a)代入，得a－(t2＋1)＝2t(1－t)，‎ 即t2－2t＋a－1＝0.‎ ‎∵切线有两条，∴方程有两个不同的解．‎ 故Δ＝4－4(a－1)>0.∴a<2.故存在实数a，使得经过点(1，a)能作出该曲线的两条切线，a的取值范围是(－∞，2)．‎