【数学】2020届一轮复习（文）人教通用版4-6正弦定理和余弦定理学案 16页

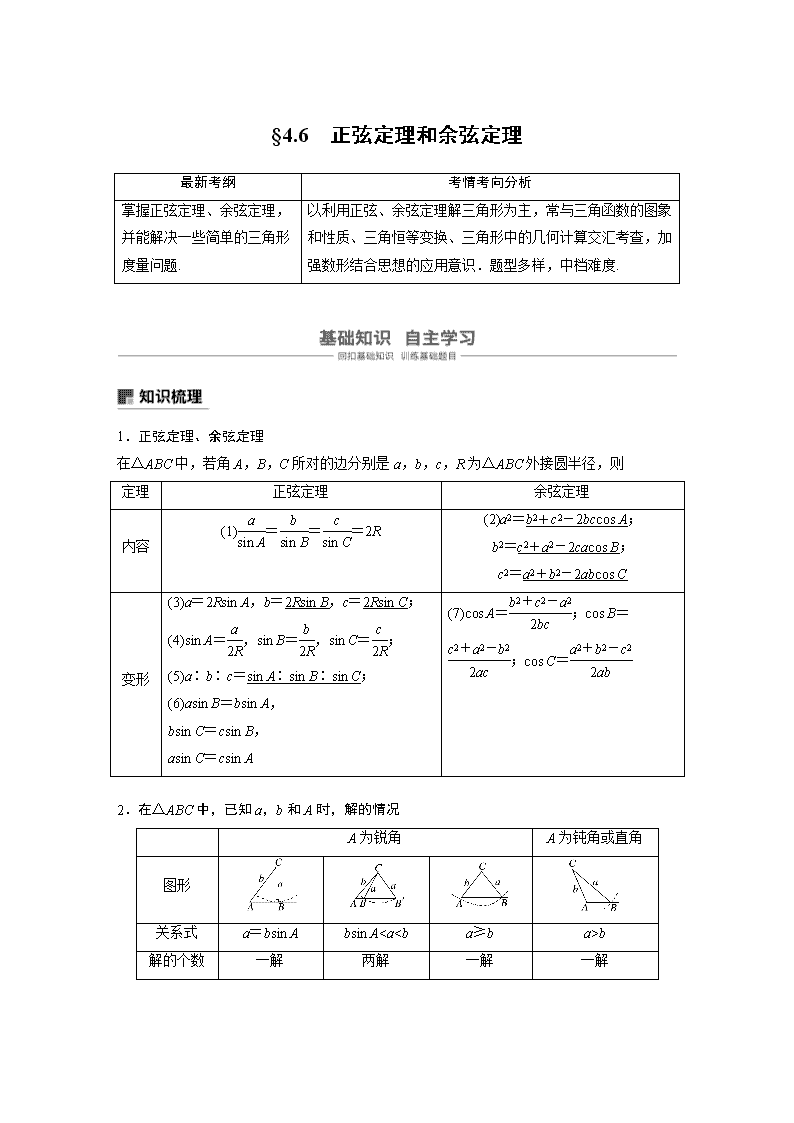
‎§4.6　正弦定理和余弦定理 最新考纲 考情考向分析 掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.‎ 以利用正弦、余弦定理解三角形为主，常与三角函数的图象和性质、三角恒等变换、三角形中的几何计算交汇考查，加强数形结合思想的应用意识．题型多样，中档难度.‎ ‎1．正弦定理、余弦定理 在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则 定理 正弦定理 余弦定理 内容 ‎(1)＝＝＝2R ‎(2)a2＝b2＋c2－2bccos A；‎ b2＝c2＋a2－2cacos B；‎ c2＝a2＋b2－2abcos C 变形 ‎(3)a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；‎ ‎(4)sin A＝，sin B＝，sin C＝；‎ ‎(5)a∶b∶c＝sin A∶sin B∶sin C；‎ ‎(6)asin B＝bsin A，‎ bsin C＝csin B，‎ asin C＝csin A ‎(7)cos A＝；cos B＝；cos C＝ ‎2．在△ABC中，已知a，b和A时，解的情况 A为锐角 A为钝角或直角 图形 关系式 a＝bsin A bsin Ab 解的个数 一解 两解 一解 一解 ‎3.三角形常用面积公式 ‎(1)S＝a·ha(ha表示边a上的高)；‎ ‎(2)S＝absin C＝acsin B＝bcsin A；‎ ‎(3)S＝r(a＋b＋c)(r为三角形内切圆半径)．‎ 概念方法微思考 ‎1．在△ABC中，∠A>∠B是否可推出sin A>sin B?‎ 提示　在△ABC中，由∠A>∠B可推出sin A>sin B.‎ ‎2．如图，在△ABC中，有如下结论：bcos C＋ccos B＝a.试类比写出另外两个式子．‎ 提示　acos B＋bcos A＝c；acos C＋ccos A＝b.‎ 题组一　思考辨析 ‎1．判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)三角形中三边之比等于相应的三个内角之比．(　×　)‎ ‎(2)当b2＋c2－a2>0时，三角形ABC为锐角三角形．(　×　)‎ ‎(3)在△ABC中，＝.(　√　)‎ ‎(4)在三角形中，已知两边和一角就能求三角形的面积．(　√　)‎ 题组二　教材改编 ‎2．在△ABC中，acos A＝bcos B，则这个三角形的形状为 ．‎ 答案　等腰三角形或直角三角形 解析　由正弦定理，得sin Acos A＝sin Bcos B，‎ 即sin 2A＝sin 2B，所以2A＝2B或2A＝π－2B，即A＝B或A＋B＝，‎ 所以这个三角形为等腰三角形或直角三角形．‎ ‎3．在△ABC中，A＝60°，AC＝4，BC＝2，则△ABC的面积为 ．‎ 答案　2 解析　∵＝，∴sin B＝1，∴B＝90°，‎ ‎∴AB＝2，∴S△ABC＝×2×2＝2.‎ 题组三　易错自纠 ‎4．在△ABC中，角A，B，C所对的边分别为a，b，c，若c0，∴cos B<0，∴B为钝角，‎ 故△ABC为钝角三角形．‎ ‎5．(2018·大连质检)在△ABC中，已知b＝40，c＝20，C＝60°，则此三角形的解的情况是(　　)‎ A．有一解 B．有两解 C．无解 D．有解但解的个数不确定 答案　C 解析　由正弦定理得＝，∴sin B＝＝＝>1.‎ ‎∴角B不存在，即满足条件的三角形不存在．‎ ‎6．(2018·包头模拟)设△ABC的内角A，B，C所对边的长分别为a，b，c.若b＋c＝2a,3sin A＝5sin B，则C＝ .‎ 答案　 解析　由3sin A＝5sin B及正弦定理，得3a＝5b.又因为b＋c＝2a，所以a＝b，c＝b，‎ 所以cos C＝＝＝－.‎ 因为C∈(0，π)，所以C＝.‎ 题型一　利用正弦、余弦定理解三角形 例1 (2018·天津)在△ABC中，内角A，B，C所对的边分别为a，b，c.已知bsin A＝acos.‎ ‎(1)求角B的大小；‎ ‎(2)设a＝2，c＝3，求b和sin(2A－B)的值．‎ 解　(1)在△ABC中，由正弦定理＝，‎ 可得bsin A＝asin B.‎ 又由bsin A＝acos，得asin B＝acos，‎ 即sin B＝cos，所以tan B＝.‎ 又因为B∈(0，π)，所以B＝.‎ ‎(2)在△ABC中，由余弦定理及a＝2，c＝3，B＝，‎ 得b2＝a2＋c2－2accos B＝7，故b＝.‎ 由bsin A＝acos，可得sin A＝.‎ 因为a0，∴sin A＝1，‎ 即A＝，∴△ABC为直角三角形．‎ 引申探究 ‎1．本例(2)中，若将条件变为2sin Acos B＝sin C，判断△ABC的形状．‎ 解　∵2sin Acos B＝sin C＝sin(A＋B)，‎ ‎∴2sin Acos B＝sin Acos B＋cos Asin B，‎ ‎∴sin(A－B)＝0.‎ 又A，B为△ABC的内角．‎ ‎∴A＝B，∴△ABC为等腰三角形．‎ ‎2．本例(2)中，若将条件变为a2＋b2－c2＝ab，且2cos Asin B＝sin C，判断△ABC的形状．‎ 解　∵a2＋b2－c2＝ab，∴cos C＝＝，‎ 又0c，可得30°0，‎ ‎∴1＝，即sin B＝cos A.‎ ‎(2)解　由sin C－sin Acos B＝知，‎ sin(A＋B)－sin Acos B＝，∴cos Asin B＝.‎ 由(1)知，sin B＝cos A，‎ ‎∴cos2A＝，由于B是钝角，‎ 故A∈，∴cos A＝，A＝.‎ sin B＝，B＝，∴C＝π－(A＋B)＝.‎ ‎12．(2018·北京)在△ABC中，a＝7，b＝8，cos B＝－.‎ ‎(1)求∠A；‎ ‎(2)求AC边上的高．‎ 解　(1)在△ABC中，因为cos B＝－，‎ 所以sin B＝＝.‎ 由正弦定理得sin A＝＝.‎ 由题设知<∠B<π，所以0<∠A<，‎ 所以∠A＝.‎ ‎(2)在△ABC中，‎ 因为sin C＝sin(A＋B)＝sin Acos B＋cos Asin B＝，‎ 所以AC边上的高为asin C＝7×＝.‎ ‎13．在△ABC中，a2＋b2＋c2＝2absin C，则△ABC的形状是(　　)‎ A．不等腰的直角三角形 B．等腰直角三角形 C．钝角三角形 D．正三角形 答案　D 解析　易知a2＋b2＋c2＝a2＋b2＋a2＋b2－2abcos C＝2absin C，即a2＋b2＝2absin，由于a2＋b2≥2ab，当且仅当a＝b时取等号，所以2absin≥2ab，sin≥1，故只能a＝b且C＋＝，所以△ABC为正三角形．‎ ‎14．(2018·包头模拟)在△ABC中，角A，B，C所对的边分别为a，b，c，且满足asin B＝bcos A．若a＝4，则△ABC周长的最大值为________．‎ 答案　12‎ 解析　由正弦定理＝，‎ 可将asin B＝bcos A转化为sin Asin B＝sin Bcos A.‎ 又在△ABC中，sin B>0，∴sin A＝cos A，‎ 即tan A＝.‎ ‎∵0