高考文科数学（北师大版）专题复习课件：第4讲 函数的概念及其表示 46页

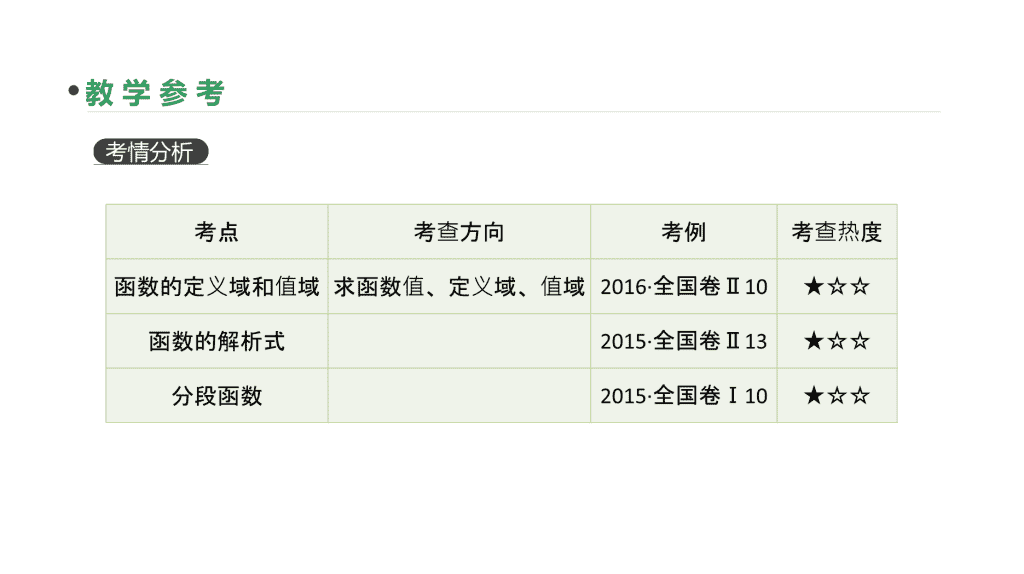
第4讲　PART 02 函数的概念及其表示 教学参考│课前双基巩固│课堂考点探究│教师备用例题 1．了解构成函数的要素，会求一些简单函数的定义域和值域；了解映射的概念． 2．在实际情境中，会根据不同的需要选择恰当的方法(如图像法、列表法、解析法)表示 函数． 3．了解简单的分段函数，并能简单应用(函数分段不超过三段)． 考试说明 考情分析 教 学 参 考 考点 考查方向 考例 考查热度 函数的定义域和值域 求函数值、定义域、值域 2016·全国卷Ⅱ10 ★☆☆ 函数的解析式 2015·全国卷Ⅱ13 ★☆☆ 分段函数 2015·全国卷Ⅰ10 ★☆☆ 真题在线 真题在线 真题在线 真题在线 真题在线 [答案] －2　1　 真题在线 函数 映射 两集合 A，B 设A，B是两个________ 设A，B是两个 ________ 对应 关系 f：A→B 如果按照某个对应关系f，对于集合 A中的________一个数x，在集合B中 都存在________的数f(x)与之对应 如果按某一个确定的对应关系 f，使对于集合A中的________ 一个元素x，在集合B中都有 ________的元素y与之对应 名称 称________为从集合A到集合B的一 个函数 称对应________为从集合A到 集合B的一个映射 记法 y＝f(x)，x∈A f：A→B 知识梳理 课前双基巩固 非空数集 非空集合 任意 唯一确定 任意 唯一确定 f：A→B f：A→B 课前双基巩固 定义域 值域 解析法 图像法 列表法 对应关系 定义域 值域 课前双基巩固 课前双基巩固 对点演练 课前双基巩固 对点演练 课前双基巩固 对点演练 课前双基巩固 对点演练 课前双基巩固 ◆ 索引：函数概念理解不透彻；分段函数解不等式忘记范围；换元法求解析式，反 解忽视范围；函数值域理解不透彻． 对点演练 课前双基巩固 对点演练 课前双基巩固 对点演练 课前双基巩固 对点演练 课前双基巩固 对点演练 课前双基巩固 探究点一　函数的定义域 课堂考点探究 考向1 求给定函数解析式的定义域 课堂考点探究 课堂考点探究 [总结反思] 对于由解析式给出的函数，其定义域可能有如下几种情况：(1)若f(x)是分式，则 其定义域是使分母不为零的全体实数组成的集合；(2)若f(x)是偶次根式，则其定 义域是使被开方数非负(即不小于零)的实数的取值集合；(3)如果函数是由一些函 数通过四则运算组合而成的，那么它的定义域是各函数定义域的交集. 课堂考点探究 课堂考点探究 考向2　求抽象函数的定义域 课堂考点探究 课堂考点探究 [总结反思] (1)若f(x)的定义域为[m，n]，则在f[g(x)]中，m≤g(x)≤n，从而解得x的范围即为 f[g(x)]的定义域；(2)若f[g(x)]的定义域为[m，n]，则由m≤x≤n确定的g(x)的范围即 为f(x)的定义域． 课堂考点探究 考向3　已知定义域确定参数问题 课堂考点探究 课堂考点探究 [总结反思] 此类问题的一般解法是：根据所给定义域，将问题转化为含参数的不等式(组)， 进而求解参数范围． 探究点二　函数的解析式 课堂考点探究 课堂考点探究 课堂考点探究 [总结反思] 函数解析式的求法： (1)换元法，已知复合函数f[g(x)]的解析式，可用换元法，此时要注意新元的取值范 围； (2)待定系数法，若已知函数的类型(如一次函数、二次函数)，可用待定系数法； (3)配凑法，由已知条件f[g(x)]＝F(x)，可将F(x)改写成关于g(x)的表达式，然后以x 替代g(x)，便得f(x)的解析式； (4)消去法，已知f(x)与f或f(－x)之间的关系式，可根据已知条件再构造出另外一个 等式组成方程组，通过解方程组求出f(x)． 课堂考点探究 探究点三　分段函数 课堂考点探究 考向1 求分段函数的函数值 课堂考点探究 课堂考点探究 [总结反思] 求分段函数的函数值时，首先要确定自变量的值属于哪个区间，再选定相应的解 析式代入计算求解，特别要注意分段区间端点的取舍． 课堂考点探究 考向2 分段函数的含参问题 课堂考点探究 课堂考点探究 [总结反思] 给出函数值或函数值的范围求自变量值或自变量的取值范围时，应根据每一段的 解析式分别求解，但要注意检验所求自变量值是否符合相应段的自变量的取值范 围． 教师备用例题 [备选理由] 例1是复合函数的定义域问题， 例2是分段函数求值问题， 例3是与分段函数有关的参数问题．希望这三个题目有助于考生对函数概念的理 解． 教师备用例题 教师备用例题 教师备用例题