- 2.02 MB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课题:平行线分线段成比例定理
l
1
l
3
l
2
l
4
l
5
l
6
A
B
C
D
E
F
M
N
O
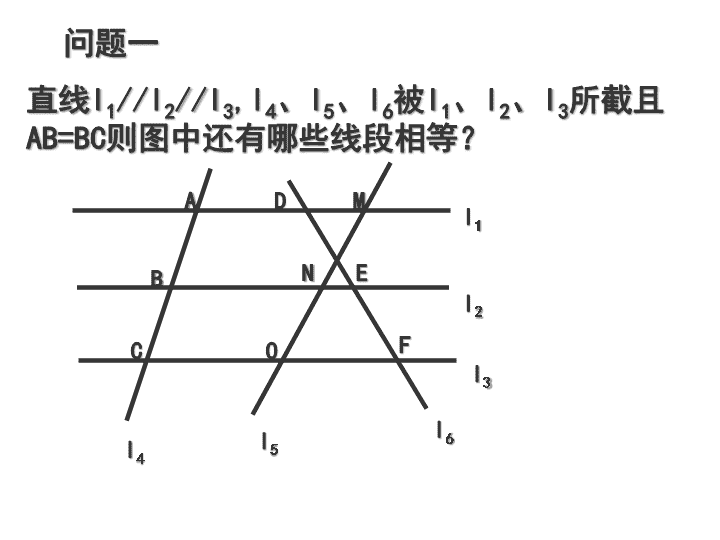
直线
l
1
//l
2
//l
3
,l
4
、
l
5
、
l
6
被
l
1
、
l
2
、
l
3
所截且
AB=BC
则图中还有哪些线段相等?
问题一
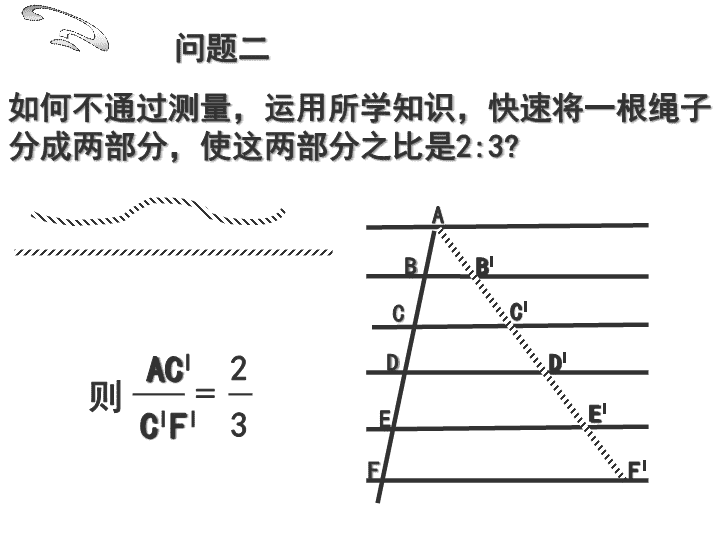
问题二
如何不通过测量,运用所学知识,快速将一根绳子分成两部分,使这两部分之比是
2:3?
A
B
C
?
E
D
F
B
I
D
I
C
I
E
I
F
I
3
2
C
I
F
I
则
=
AC
I
A
B
C
E
D
F
B
I
D
I
C
I
E
I
F
I
3
2
=
C
I
F
I
AC
I
CF
A
C
=
3
1
=
C
I
F
I
B
I
C
I
CF
B
C
=
BF
B
C
4
1
B
I
F
I
=
B
I
C
I
=
A
B
C
E
D
F
B
I
D
I
C
I
E
I
F
I
A
B
C
E
D
F
B
I
A
I
D
I
C
I
E
I
F
I
AD
D
F
3
2
A
I
D
I
=
D
I
F
I
=
AF
D
F
5
2
A
I
F
I
=
D
I
F
I
=
平行线分线段成比例定理:
三条平行线截两条直线,所得的
线段
成比例
.
对应
怎样用文字把以上发现表述出来?
A
B
C
D
E
F
l
1
l
3
l
2
.
.
.
.
.
.
.
.
形象记忆
A
B
C
D
E
F
l
1
l
3
l
2
3
?
4
2
[
例一
]
(平行线分线段成比例
定理)
6
BC
=
4
2
BC
3
即
=
EF
DE
BC
AB
=
//l
//l
l
解:
3
2
1
Q
A
B
C
D
E
F
l
1
l
3
l
2
[
例二
]
注意观察:
此图与前面图形有何不同?
A
B
C
D
E
F
(平行线分线段成比例定理)
.
n
m
m
DF
DE
+
=
.
m
n
m
DE
DF
即
+
=
,
m
m
n
DE
DE
EF
+
=
+
m
n
DE
EF
=
n
m
EF
DE
BC
AB
=
=
,
//l
//l
l
3
2
1
Q
:
证明
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
l
1
l
3
l
2
?
[
练习一
]
求:
DE.
c.
EF
b,
BC
a,
,
AB
//l
//l
已知:如图,
l
3
2
1
=
=
=
l
1
l
3
l
2
[
练习二
]
A
B
C
D
E
F
DE
AB
求证:
//l
//l
已知:如图,
l
3
2
1
=
EF
BC
=
DF
AC
如图,有一块形状为直角梯形的草地,周围均为水泥直道,两个拐角
A
、
B
处均为直角,草地中间另有一条水泥直道
EF
垂直于
AB
,垂足为
E.
已知
AE
长
a
米,
EB
长
b
米,
DF
长
c
米
.
求
CF.
A
B
C
D
E
F
a
b
c
?
米
.
a
bc
答:
CF
长为
a
bc
CF
CF
c
b
a
即
定理)
(平行线分线段成比例
CF
DF
EB
AE
AD//EF//BC
B
,
EF
90
ABC
DAB
解:由题意可知:
0
=
=
=
^
=
Ð
=
Ð
A
对题目的再思考
!
C
F
A
B
D
E
若是三角形草地呢?(
EF//BC
)
定理还能用吗?
A
B
E
C
F
如上图:
AE=3
,
AF=6
,
EB=4.
求
FC.
6
3
4
?
8
三条平行线截两条直线,所得的
对应线段
成比例
.
平行线分线段成比例定理与平行线等分线段
定理有何联系?
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
平行线分线段成比例定理:
课 堂 小 结
要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
A
B
C
D
E
课后思考题
如图:若
AB//CD
,
平行线分线段成比例定理
还能用吗?
A
B
C
D
E