高中数学选修2-3公开课课件3_1回归分析的基本思想及其初步应用（1） 19页

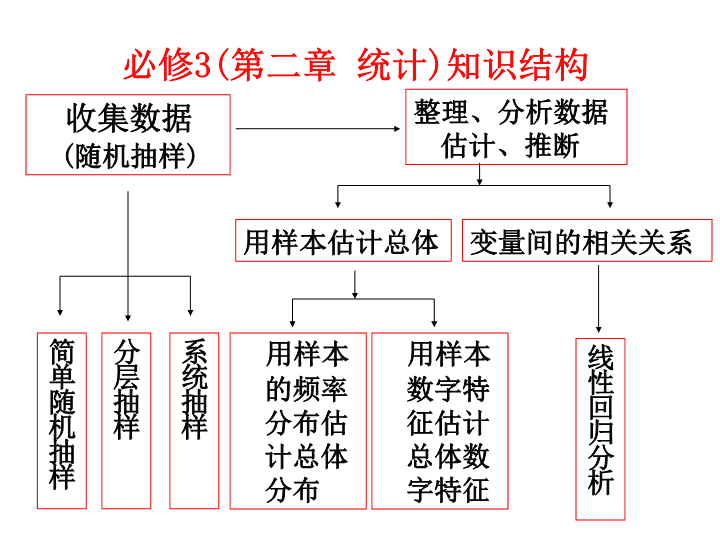
3.1《 回归分析的基本思想及其初步应用 》 教学目标 通过典型案例，掌握回归分析的基本步骤。 教学重点 ：熟练掌握回归分析的步骤。 教学难点 ：求回归系数 a , b 教学方法 ：讲练。 必修 3( 第二章 统计 ) 知识结构 收集数据 ( 随机抽样 ) 整理、分析数据估计、推断 简单随机抽样 分层抽样 系统抽样 用样本估计总体 变量间的相关关系 用样本的频率分布估计总体分布 用样本数字特征估计总体数字特征 线性回归分析 统计的基本思想 实际 样本 模 拟 抽 样 分 析 1 、两个变量的关系 不相关 相关关系 函数关系 线性相关 非线性相关 问题 1 ：现实生活中两个变量间的关系有哪些呢？ 相关关系： 对于两个变量，当自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系。 思考 ：相关关系与函数关系有怎样的不同？ 函数关系中的两个变量间是一种确定性关系 相关关系是一种非确定性关系 函数关系是一种理想的关系模型 相关关系在现实生活中大量存在，是更一般的情况 问题 2 ：对于线性相关的两个变量用什么方法来刻划之间的关系呢？ 2 、最小二乘估计 最小二乘估计下的线性回归方程： 对一作直线运动的质点的运动过程作了 8 次观测，得到下表，试估计 x=9s 时的位置 y 的值。 时刻 x/s 1 2 3 4 5 6 7 8 位置观测值 y/cm 5.54 7.52 10.02 11.73 15.69 16.12 16.98 21.06 例如： i 1 2 3 4 5 6 7 8 x i 1 2 3 4 5 6 7 8 4.50 y i 5.54 7.52 10.02 11.73 15.69 16.12 16.98 21.06 13.08 x i y i 5.54 15.04 30.06 46.92 78.45 96.72 118.9 168.5 560.1 x i 2 1 4 9 16 25 36 49 64 204 3 、 回归分析的基本步骤 : 画散点图 求回归方程 预报、决策 数学３ —— 统计 画散点图 求出 b,a 的值。 求回归直线方程 用回归直线方程解决应用问题 4 、 线性回归模型 其中 a+bx 是确定性函数，  是随机误差 注： 产生的主要原因： (1) 所用确定性函数不恰当； (2) 忽略了某些因素的影响； (3) 观测误差。 思考 ：在时刻 x=9s 时，质点运动位置一定是 22.6287cm 吗？ 对于线性回归模型 应注意以下两个问题： I 模型的合理性； II 在模型合理的情况下，如何估计 a,b. 例 1. 下表给出我国从 1949 至 1999 年人口数 据资料，试根据表中数据估计我国 2004 年 的人口数。 年份 49 54 59 64 69 74 79 84 89 94 99 人口数 / 百万 542 603 672 705 807 909 975 1035 1107 1177 1246 年份 0 5 10 15 20 25 30 35 40 45 50 人口数 / 百万 542 603 672 705 807 909 975 1035 1107 1177 1246 分析：先画图 例题 2. 一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了 10 次试验，测得数据如下： 零件数（ x ）个 10 20 30 40 50 60 70 80 90 100 加工时间 y 62 68 75 81 89 95 102 108 115 122 (1)y 与 x 是否具有线性相关？ (2) 若 y 与 x 具有线性相关关系，求回归直线方程 (3) 预测加工 200 个零件需花费多少时间？ 分析：这是一个回归分析问题，应先进行线性相关检验或作散点图来判断 x 与 y 是否具有线性相关才可以求解后面的问题。 作散点图如下： 不难看出 x,y 成线性相关。 解 （ 1 ）列出下表： i 1 2 3 4 5 6 7 8 9 10 x i 10 20 30 40 50 60 70 80 90 100 y i 62 68 75 81 89 95 102 108 115 122 x i y i 620 1360 2250 3240 4450 5700 7140 8640 10350 12200 问题 ：有时散点图的各点并不集中在一条直线的附近，仍然可以按照求回归直线方程的步骤求回归直线，显然这样的回归直线没有实际意义。 在怎样的情况下求得的回归直线方程才有实际意义？ 即建立的线性回归模型是否合理 ？ 如何对一组数据之间的线性相关程度作出定量分析？ 请看下节课分解 再见