新课标版高考数学复习题库考点16 不等式 12页

‎ ‎ 考点16 不等式 ‎ ‎1.（2010·安徽高考文科·Ｔ8）设x,y满足约束条件则目标函数z=x+y的最大值是（ ）‎ ‎（A）3 （B） 4 （C） 6 （D）8‎ ‎【命题立意】本题主要考查线性规划问题，考查考生的作图、运算求解能力.‎ ‎【思路点拨】由约束条件画可行域确定目标函数的最大值点计算目标函数的最大值 ‎【规范解答】选C．约束条件表示的可行域是一个三角形区域，3个顶点分别 是，目标函数在取最大值6，故C正确．‎ ‎【方法技巧】解决线性规划问题，首先作出可行域，若为封闭区域（即几条直线围成的区域），则区域中的某个端点使目标函数取得最值． ‎ ‎2.（2010·福建高考文科·Ｔ5）若，且，则的最小值等于（ ）‎ ‎(A)2 (B)3 (C)5 (D)9‎ ‎【命题立意】本题考查利用线性规划的方法求最值． ‎ ‎【思路点拨】先画出不等式组表示的线性区域，再作出直线，平移，当其截距越小，的值越小．‎ ‎【规范解答】选B．不等式组所表示的平面区域如图阴影所示：‎ 作，平移至点位置时，取得最小值，即． ‎ ‎【方法技巧】‎ 本题可以采用多种解法，有些解法一反常规，‎ 颠覆视觉．‎ 方法一（特殊点法）：因为直线两两相交分别 交于，当时，；‎ 当时，；当时，；‎ 所以当时，．‎ 方法二（反代入法）：，把代入得：‎ 所以有最小值3．‎ 方法三（向量法）：设，则 方向上的投影，所以当在位置时取得最小值，所以当时，为最小值． ‎ ‎3.（2010·浙江高考文科·Ｔ7）若实数x,y满足不等式组，则x+y的最大值为（ ）‎ ‎（A）9 （B） （C）1 （D）‎ ‎【命题立意】本题主要考查了平面区域的二元一次不等式组，以及简单的转化思想和数形结合的思想，‎ 属中档题．‎ ‎【思路点拨】画出不等式组表示的平面区域，再利用图象求的最大值．‎ ‎【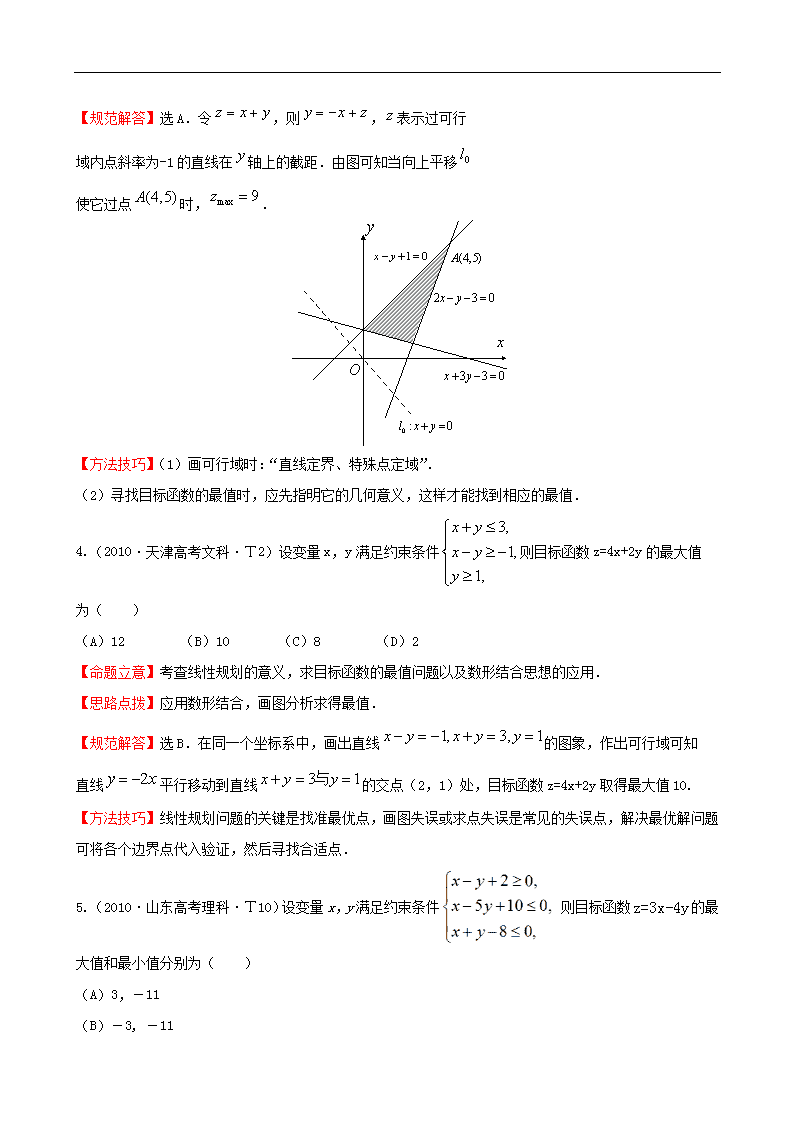规范解答】选A．令，则，表示过可行 域内点斜率为-1的直线在轴上的截距．由图可知当向上平移 使它过点时，．‎ ‎【方法技巧】（1）画可行域时：“直线定界、特殊点定域”．‎ ‎（2）寻找目标函数的最值时，应先指明它的几何意义，这样才能找到相应的最值． ‎ ‎4.（2010·天津高考文科·Ｔ2）设变量x，y满足约束条件则目标函数z=4x+2y的最大值 为（ ）‎ ‎（A）12 （B）10 （C）8 （D）2‎ ‎【命题立意】考查线性规划的意义，求目标函数的最值问题以及数形结合思想的应用．‎ ‎【思路点拨】应用数形结合，画图分析求得最值．‎ ‎【规范解答】选B．在同一个坐标系中，画出直线的图象，作出可行域可知 直线平行移动到直线的交点（2，1）处，目标函数z=4x+2y取得最大值10.‎ ‎【方法技巧】 线性规划问题的关键是找准最优点，画图失误或求点失误是常见的失误点，解决最优解问题可将各个边界点代入验证，然后寻找合适点． ‎ ‎5.（2010·山东高考理科·Ｔ10）设变量x，y满足约束条件则目标函数的最大值和最小值分别为（ ）‎ ‎（A）3，－11 ‎ ‎（B）－3, －11‎ ‎（C）11, －3 ‎ ‎（D）11,3‎ ‎【命题立意】本题考查不等式中的线性规划知识及数形结合的数学思想、考查了考生的推理论证能力和运算求解能力.‎ ‎【思路点拨】先画出不等式组所表示的平面区域，再求解.‎ ‎【规范解答】选A ．画出平面区域如图所示：可知当平移到点（5，3）时，目标函数取得最大值3；当平移到点（3，5）时，目标函数取得最小值-11，故选A. ‎ ‎6.（2010·浙江高考理科·Ｔ7）若实数，满足不等式组且的最大值为9，‎ 则实数（ ）‎ ‎（A） （B） （C）1 （D）2‎ ‎【命题立意】本题考查线性规划的相关知识，考查数形结合思想．‎ ‎【思路点拨】画出平面区域，利用的最大值为9，确定区域的边界．‎ ‎【规范解答】选C．令，则，表示斜率为-1的直线在轴上的截距．‎ 当最大值为9时，过点A，因此过点A，所以．‎ ‎【方法技巧】画平面区域时“直线定界、特殊点定域”．‎ ‎7.（2010·北京高考理科·Ｔ7）设不等式组表示的平面区域为D，若指数函数y=的图象上存在区域D上的点，则a 的取值范围是（ ）‎ ‎（A）(1,3] (B)[2,3] (C) (1,2] (D)[ 3, )‎ ‎【命题立意】本题考查平面区域，指数函数的相关知识．‎ ‎【思路点拨】画出平面区域D，再观察的图象．‎ ‎【规范解答】选A．区域D如图所示，其中．当恰过点A时，．‎ 因此当时，的图象上存在区域D上的点．‎ ‎【方法技巧】画区域D时可采用“直线定界、特殊点定域”的方法．‎ ‎8.（2010·江苏高考·Ｔ１2）设x,y为实数，满足3≤≤8，4≤≤9，则的最大值是 ．‎ ‎【命题立意】本题考查不等式的基本性质，等价转化思想．‎ ‎【思路点拨】‎ ‎【规范解答】，，，‎ 的最大值是27．‎ ‎【答案】27‎ ‎9.（2010·浙江高考文科·Ｔ16） 某商家一月份至五月份累计销售额达3 860万元，预测六月份销售额为500万元，七月份销售额比六月份递增x%，八月份销售额比七月份递增x%，九、十月份销售总额与七、八月份销售总额相等，若一月至十月份销售总额至少达7 000万元，则x的最小值为 ．‎ ‎【命题立意】本题主要考查了用一元二次不等式解决实际问题的能力，属中档题．‎ ‎【思路点拨】把一到十月份的销售额求和，列出不等式，求解．‎ ‎【规范解答】七月份：，八月份：．所以一至十月份的销售总额为：‎ ‎，解得（舍）或，‎ ‎．‎ ‎【答案】20‎ ‎10.（2010·浙江高考文科·Ｔ15）若正实数，满足，则的最小值是 ．‎ ‎【命题立意】本题主要考查了用基本不等式解决最值问题的能力 ，以及换元思想和简单一元二次不等式的解法，属中档题．‎ ‎【思路点拨】本题可利用基本不等式构造出关于的不等式，解出的最小值．‎ ‎【规范解答】运用基本不等式，，令，可得，注意到t＞0，解得t≥,故xy的最小值为18．‎ ‎【答案】18‎ ‎【方法技巧】基本不等式有两个常用变形：（1）当和为定值时，积有最大值，即．（2）当积为定值时，和有最小值，即．‎ ‎11.（2010·山东高考文科·Ｔ１4）已知R+，且满足，则xy的最大值为 .‎ ‎【命题立意】本题考查均值定理，考查考生运用基本不等式运算求解能力.‎ ‎【规范解答】R+，且，由基本不等式有，解得，‎ 当且仅当，即时，等号成立，所以xy的最大值为3.‎ ‎【答案】3‎ ‎12.（2010·山东高考理科·Ｔ14）若对任意，恒成立，则的取值范围是 ．‎ ‎【命题立意】本题考查了利用基本不等式求最值及不等式恒成立问题以及参数问题的求解，考查了考生的转化能力和运算求解能力．‎ ‎【思路点拨】将恒成立问题转化为最值问题.‎ ‎【规范解答】因为，所以（当且仅当时取等号），所以有 ‎，即的最大值为，故 .‎ ‎ 【答案】‎ ‎【方法技巧】1．不等式的恒成立问题与函数最值有密切的关系，解决不等式恒成立问题，通常先分离参数，再转化为最值问题来解：‎ 恒成立；‎ 恒成立．‎ ‎2．高次函数或非基本初等函数的最值问题，通常采用导数法解决.‎ ‎13.（2010·安徽高考文科·Ｔ15）若，则下列不等式对一切满足条件的恒成立的是 (写出所有正确命题的编号)．‎ ‎①； ②； ③ ； ‎ ‎④； ⑤．‎ ‎【命题立意】本题主要考查均值定理，考查考生变形转化的能力．‎ ‎【思路点拨】可以利用特值排除，结合均值定理变形转化求解．‎ ‎【规范解答】令，排除②，④；‎ 由，命题①正确；‎ 由，命题③正确；‎ 由，命题⑤正确．‎ ‎【答案】①③⑤‎ ‎14.（2010·陕西高考文科·Ｔ１4）设x，y满足约束条件则目标函数z＝3x－y的最大值为 .‎ ‎【命题立意】本题考查不等式中的线性规划知识，‎ 画出平面区域与正确理解目标函数的几何意义是 解答好本题的关键，属中档题．‎ ‎【思路点拨】作出可行域作出直线3x－y＝0‎ 平移3x-y=0结论 ‎【规范解答】作出可行域 当目标函数z＝3x－y过点A时，z取到最大值5.‎ ‎【答案】５‎ ‎15.（2010·北京高考文科·Ｔ11）若点P（m，3）到直线的距离为4，且点P在不等式 ‎＜3表示的平面区域内，则m= ．‎ ‎【命题立意】本题考查了点到直线的距离与线性规划的知识．‎ ‎【思路点拨】先利用点到直线的距离求出，再把所得点P的坐标代入到不等式中去验证．‎ ‎【规范解答】点P（m，3）到直线的距离为4，解得或m=．又因为点P在不等式＜3表示的平面区域内，所以．‎ ‎【答案】-3‎ ‎【方法技巧】判断点是否在某平面区域内，只需把点的坐标代入到不等式(组)中看是否成立即可．‎ ‎16.（2010·安徽高考理科·Ｔ13）设满足约束条件 若目标函数的最大值为8，则的最小值为________．‎ ‎【命题立意】本题主要考查线性规划问题和均值定理，考查考生的作图、运算求解能力．‎ ‎【思路点拨】由约束条件画可行域 确定目标函数的最大值点计算的值 ‎ 利用均值定理计算的最小值 ‎【规范解答】 已知满足约束条件，其可行域是一个四边形，4个顶点的坐标分别是 ‎，易得目标函数在点处取最大值8，‎ 所以，即，，当且仅当时，等号成立．‎ 所以的最小值为4．‎ ‎【答案】4‎ ‎【方法技巧】线性规划问题首先作出可行域，若为封闭区域（即几条直线围成的区域），则目标函数的最大或最小值在区域的端点或边界处取得．‎ ‎17.（2010·辽宁高考理科·Ｔ14）已知且，则的取值范围 是_______（答案用区间表示）．‎ ‎【命题立意】本题考查线性规划问题．‎ ‎【思路点拨】‎ 写出答案 利用性质求出范围 作出可行域 ‎【规范解答】作出可行域（如图），‎ 将目标函数z=2x-3y变形为，它表示与平行，截距是的一组平行直线，当它经过点A时，截距最大，此是z取得最小值；当经过点B时，截距最小，此时z最大．由 由 ‎∴z=2x－３y的取值范围是（3，8）．‎ ‎【答案】（3，8）‎ ‎【方法技巧】本题还可设，利用不等式求解．注意：不要先分别求，‎ 的范围再求的范围，这样会将范围扩大，导致结果错误．‎ ‎18.（2010·陕西高考理科·Ｔ１4）铁矿石A和B的含铁率为,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石的价格c如下表：‎ b(万吨)‎ ‎（百万元）‎ A ‎50%‎ ‎1‎ ‎3‎ B ‎70%‎ ‎0．5‎ ‎6‎ 某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用 为_　　_ (百万元)．‎ ‎【命题立意】本题考查不等式中的线性规划知识的应用，画出平面区域与正确理解目标函数的几何意义是解答好本题的关键．属中档题．‎ ‎【思路点拨】设购买铁矿石A，B分别为万吨线性约束条件最优解结论．‎ ‎【规范解答】设购买铁矿石A，B分别为万吨，购买铁矿石的费用为z（百万元），则 ‎，目标函数，，‎ 画出可行域可知，当目标函数过点P（1，2）时，z取到最小值15.‎ ‎【答案】15‎ ‎19.（2010·广东高考文科·Ｔ19）某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12‎ 个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素．一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素.另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素.‎ 如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐?‎ ‎【命题立意】本题为应用题，考查简单的线性规划问题以及建立数学模型的方法.‎ ‎【思路点拨】建立目标函数列出约束条件画出可行域求目标函数的最值.‎ ‎【规范解答】设为该儿童分别预定个单位的午餐和晚餐，共需元，则 ‎.‎ 作出可行域如图：‎ 所以，当时，花费最少，为 ‎（元）.‎ 答：应当为该儿童分别预定4个午餐和3个晚餐.‎ ‎【方法技巧】线性规划的应用问题，应从目标函数入手，列出约束条件，再根据约束条件画出可行域，这样思路更清晰.‎ ‎20.（2010·广东高考理科·Ｔ19） 某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C.一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素C.‎ 如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预定多少个单位的午餐和晚餐？‎ ‎【命题立意】本题为应用题，考查简单的线性规划问题以及建立数学模型的方法.‎ ‎【思路点拨】建立目标函数列出约束条件画出可行域求目标函数的最值.‎ ‎【规范解答】设为该儿童分别预定个单位的午餐和晚餐，共需元，则.‎ 作出可行域如图：‎ 所以，当时，花费最少，为(元).‎ 答：应当为该儿童分别预定4个午餐和3个晚餐.‎ ‎【方法技巧】线性规划的应用问题，应从目标函数入手，列出约束条件，再根据约束条件画出可行域，这样思路更清晰. ‎