江西省萍乡市莲花县莲花中学2019-2020学年高二5月月考数学（文）试卷 12页

江西省萍乡市莲花县莲花中学2019-2020学年高二5月月考数学（文）试卷 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．已知集合M＝{y｜y＝3x}，N＝{｜}，则M∩N＝‎ A．{x｜0＜x＜1} B．{x｜0＜x≤1} ‎ C．{x｜x≤1} D．{x｜x＞0}‎ ‎2．已知复数z＝（a＋2i）（1－i）（a∈R）为纯虚数，则a的值为 ‎ A．1 B．－1 C．2 D．－2‎ ‎3．某单位为了落实“绿水青山就是金山银山”的理念，制定节能减排的目标，先调查了用电量y（单位：千瓦·时）与气温x（单位：℃）之间的关系，根据表中的数据由最小二乘法求得回归直线方程为，现发现表中有个数据看不清，请你推断该数据为 ‎ A．36 B．38 C．42 D．60‎ ‎4．已知点A，C是半径为1的圆O上的两个动点，则·的最大值为 ‎ A． B．1 C． D．2‎ ‎5．复数z＝i2019（－1+2i）的共轭复数为 A．2－i B．2＋i C．－2－i D．－2＋i ‎6．从[－6，10]中任取一个点m，则直线3x＋4y＋m＝0被圆x2＋y2＝2截得的弦长大于2的概率为 A． B． ‎ C． D．‎ ‎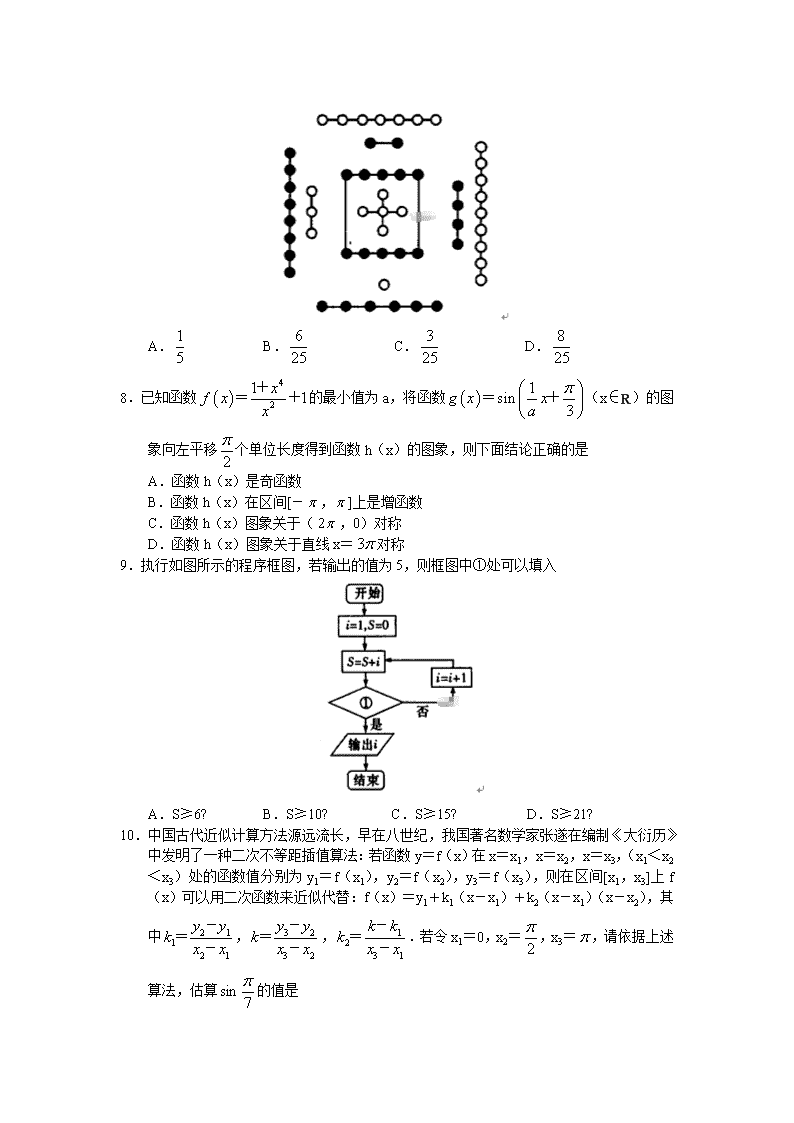7．《易·系辞上》有“河出图，洛出书”之说，河图、洛书是中国古代流传下来的两幅神秘图案，蕴含了深奥的宇宙星象之理，被誉为“宇宙魔方”，是中华文化，阴阳术数之源，其中河图的排列结构是一、六在后，二、七在前，三、八在左，四、九在右，五、十背中，如图，白圈为阳数，黑点为阴数，若从阴数和阳数中各取一数，则其差的绝对值为7的概率为 A． B． C． D．‎ ‎8．已知函数的最小值为a，将函数（x∈R）的图象向左平移个单位长度得到函数h（x）的图象，则下面结论正确的是 ‎ A．函数h（x）是奇函数 ‎ B．函数h（x）在区间[－，]上是增函数 ‎ C．函数h（x）图象关于（，0）对称 ‎ D．函数h（x）图象关于直线x＝对称 ‎9．执行如图所示的程序框图，若输出的值为5，则框图中①处可以填入 A．S≥6? B．S≥10? C．S≥15? D．S≥21?‎ ‎10．中国古代近似计算方法源远流长，早在八世纪，我国著名数学家张遂在编制《大衍历》中发明了一种二次不等距插值算法：若函数y＝f（x）在x＝x1，x＝x2，x＝x3，（x1＜x2＜x3）处的函数值分别为y1＝f（x1），y2＝f（x2），y3＝f（x3），则在区间[x1，x3]上f（x）可以用二次函数来近似代替：f（x）＝y1＋k1（x－x1）＋k2（x－x1）（x－x2），其中，，．若令x1＝0，x2＝，x3＝，请依据上述算法，估算的值是 ‎ A． B．‎ C． D．‎ ‎11．已知f（x）是定义在（－，）上的奇函数，其导函数为，，且当x∈（0，）时，，则不等式f（x）sinx＜1的解集为 ‎ A．（－，） B．（－，） C．（－，） D．（－，）‎ ‎12．19世纪法国著名数学家傅立叶（Jean Baptiste Joseph Fourier，1768－1830）证明了所有的乐声——不管是器乐还是声乐都能用数学表达式来描述，它们是一些简单的正弦周期函数的和；用器乐演奏的经典名曲《梁祝》便是如此．若某一器乐演奏曲的乐声函数是f（x）＝sinx＋asin2x，关于函数f（x）的四个结论：①无论a为何值，f（x）总是周期函数；②当0＜a＜时，函数f（x）在[0，]上为增函数；③直线x＝是函数f（x）的一条对称轴；④当a＝时，f（x）最小值为－．‎ ‎ 其中正确结论的个数为 ‎ A．4个 B．3个 C．2个 D．1个 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13．曲线f（x）＝3x3－x－2019在点（0，f（0））处的切线方程在x轴上的截距为__________．‎ ‎14．若特称命题：“，使得成立”是假命题，则实数m的取值范围__________．‎ 15. 动点在边长为2的正方形内运动，则的概率为 ．‎ ‎16．已知直线l：y＝－2x＋n与双曲线（a＞0，b＞0）的右支交于A，B两点，点B在x轴上方，B，C关于原点对称，若tan∠BAC＝，则双曲线的离心率为__________．‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎（一）必考题：60分。‎ ‎17．（12分）世界军人运动会，简称“军运会”，每四年举办一届，会期7到10天，比赛设有27个大项，参赛规模约100多个国家近10000余人，规模仅次于奥运会．根据各方达成共识，军运会于‎2019年10月18日至27日在湖北武汉举行，赛期10天，为了军运会顺利召开，特招聘了3万名志愿者．某部门为了了解志愿者的基本情况，调查了其中100名志愿者的年龄，得到了他们年龄的中位数为34岁，年龄在[40，45）岁内的人数为15人，并根据调查结果画出如图所示的频率分布直方图：‎ ‎（1）求m，n的值并估算出志愿者的平均年龄（同一组的数据用该组区间的中点值代表）；‎ ‎（2）这次军运会志愿者主要通过直接到武汉军运会执委会志愿者部现场报名和登录第七届世界军运会官网报名，即现场和网络两种方式报名．调查这100位志愿者的报名方式部分数据如下表所示，完善下面的表格，通过计算说明能否在犯错误的概率不超过0．001的前提下，认为“选择哪种报名方式与性别有关系”?‎ ‎18．（12分）某种产品的以往各年的宣传费用支出xi（万元）与销售量ti（万件）之间有如下对应数据：‎ ‎ 用最小二乘法求得线性回归直线方程是，记，我们把叫第i年的随机误差，记y1，y2，y3，y4，y5的标准差为σ．‎ ‎ （1）计算y1，y2，y3，y4，y5的方差σ2；‎ ‎ （2）从这五年中任意选2年，计算这两年随机误差的绝对值都小于σ的概率．‎ ‎19.（12分）甲材料随温度的变化会膨胀和收缩．经测试统计，得到不同温度（）时的膨胀系数的数据如下表：‎ 温度()‎ ‎22‎ ‎14‎ ‎2‎ ‎15‎ ‎34‎ 膨胀系数 ‎2.1‎ ‎1.0‎ ‎0‎ ‎0.5‎ ‎0.9‎ ‎ (Ⅰ) 膨胀系数与温度是否具有较强的线性相关性？若是，求其线性回归方程(系数精确到0.01)；‎ ‎(Ⅱ)若用非线性回归模型模拟与的相关关系，试问(Ⅰ)所得线性模型与此非性模型这两种模型的模拟效果哪一个更好？请说明理由；‎ ‎(Ⅲ)利用以上两者中模拟效果较好的模型，预报这种材料在时的膨胀系数．‎ 附：回归直线的斜率和截距的最小二乘法估计分别为：‎ ‎ ，.‎ 线性相关系数 ，贡献率 一些数据的计算值：‎ 项目 值 ‎3‎ ‎0.34‎ ‎102.8‎ ‎2020‎ ‎8.0‎ ‎45.0‎ ‎2.8‎ ‎20.（12分）已知椭圆的离心率为，点为坐标原点，椭圆与曲线的交点分别为，且．‎ ‎（Ⅰ）求此椭圆的方程；‎ ‎（Ⅱ）若过点的直线与该椭圆交于两点, 椭圆与轴交于,两点（如图），记与的面积分别为和，求的最大值.‎ ‎21．（12分）已知函数f（x）＝ex＋sinx，x∈[－，＋∞）．‎ ‎（1）若f（x）＝ex＋sinx，当x∈[0，＋∞）时，解关于x的不等式f（2x2－1）＞f（x）；‎ ‎ （2）证明：f（x）有且仅有2个零点．‎ 请考生在第22，23两题中任选一题做答.只能做所选定的题目.如果多做，则按所做的第一个题记分.做答时用2B铅笔在答题卡上把所选题号后方框涂黑.　　　　　　　‎ ‎（22）（本小题满分10分）选修4—4：坐标系与参数方程 在平面直角坐标系中，直线：(为参数)，在以为极点，轴正半轴为极轴的极坐标系中，曲线：‎ ‎（Ⅰ）求曲线的直角坐标方程和直线的普通方程；‎ ‎（Ⅱ）已知点，若直线与曲线交于，两点，求的值．‎ ‎（23）（本小题满分10分）选修4—5：不等式选讲 已知函数.‎ ‎（Ⅰ）若，求的最大值；‎ ‎（Ⅱ）当时，恒成立，求的取值范围.‎ 参考答案 一． 选择题 5. A 6.D 7.C ‎8.D 10. C ‎ 13. ‎-2019 ‎ ‎15.‎ ‎17.‎ ‎18.‎ ‎19. (Ⅰ) 线性相关系数 …………………（2分）‎ 较接近于１，因此，与有较强的线性相关性.……………………………………（3分）‎ ‎（画出了散点图，并得出与有较强的线性相关性，给2分．）‎ 由于，故设关于的线性回归方程有意义，‎ 其中， ………………………………………………（4分）‎ ‎……………………………………………………………（5分）‎ 故，所求线性回归方程为．…………………………………………………（6分）‎ ‎(Ⅱ)对非性回归模型模拟,有 ‎ ()‎ ‎22‎ ‎14‎ ‎2‎ ‎15‎ ‎34‎ ‎2‎ ‎1‎ ‎0‎ ‎0.50‎ ‎1‎ ‎………………………………………………（7分）‎ ‎．………………………………（9分）‎ 由于，，故的模拟效果更好．……………（10分）‎ ‎ (Ⅲ) 将代入，有．‎ 甲材料在时的澎涨系数的预报值为．…………………………………………………（12分）‎ ‎20. （Ⅰ）设椭圆的半焦距为，不仿设，则，…………………（1分）‎ 由，得，…………………………………………………………（2分）‎ ‎∴点在椭圆上，即，……………………………………………………（3分）‎ 又，，……………………………………………………………………………………（4分）‎ 且，得，……………………………………………………（5分）‎ 故椭圆的方程为．…………………………………………………………………（6分）‎ ‎（II）设，，显然，异号．设直线方程为，（7分）‎ 由得，‎ 显然，方程有实根，且，………………………………………………（8分）‎ 因此，………………………………… (10分)‎ ‎，………………………………………………………………（11分）‎ 当且仅当时等号成立，∴的最大值为.………………………………（12分）‎ ‎22. (Ⅰ) 有……………………………………………………………（1分）‎ 所以,,即曲线的方程为：.……………………………………（3分）‎ 直线：为参数），消去,得直线的方程为：.………………（5分）‎ ‎(Ⅱ)将 代入,得,………………………………(6分)‎ 得.……………………………………………………………………………………（7分）‎ 因，由的几何意义，得 ‎.………………………………………………………………（10分）‎ ‎23.（Ⅰ）…………………………………………………………（3分） ‎ 所以,. ……………………………………………………………………（5分）‎ ‎（II）. ……………………（8分）‎ 要使时恒成立，必………………………………………………（9分）‎ 即. …………………………………………………………………………………………（10分）‎