【数学】2019届一轮复习全国经典版（理）坐标系学案 13页

第1讲　坐标系 板块一　知识梳理·自主学习 ‎[必备知识]‎ 考点1　坐标变换 平面直角坐标系中的坐标伸缩变换 设点P(x，y)是平面直角坐标系中的任意一点，在变换φ：的作用下，点P(x，y)对应到点P′(x′，y′)，称φ为平面直角坐标系中的坐标伸缩变换，简称伸缩变换．‎ 考点2　极坐标与直角坐标 ‎1．极坐标系：在平面内取一个定点O，叫做极点，自极点O引一条射线Ox，叫做极轴；再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，就建立了极坐标系．‎ ‎2．点的极坐标：对于极坐标系所在平面内的任一点M，若设|OM|＝ρ(ρ≥0)，以极轴Ox为始边，射线OM为终边的角为θ，则点M可用有序数对(ρ，θ)表示．‎ ‎3．极坐标与直角坐标的互化公式：在平面直角坐标系xOy中，以O为极点，射线Ox的正方向为极轴方向，取相同的长度单位，建立极坐标系．设点P的直角坐标为(x，y)，它的极坐标为(ρ，θ)，则相互转化公式为 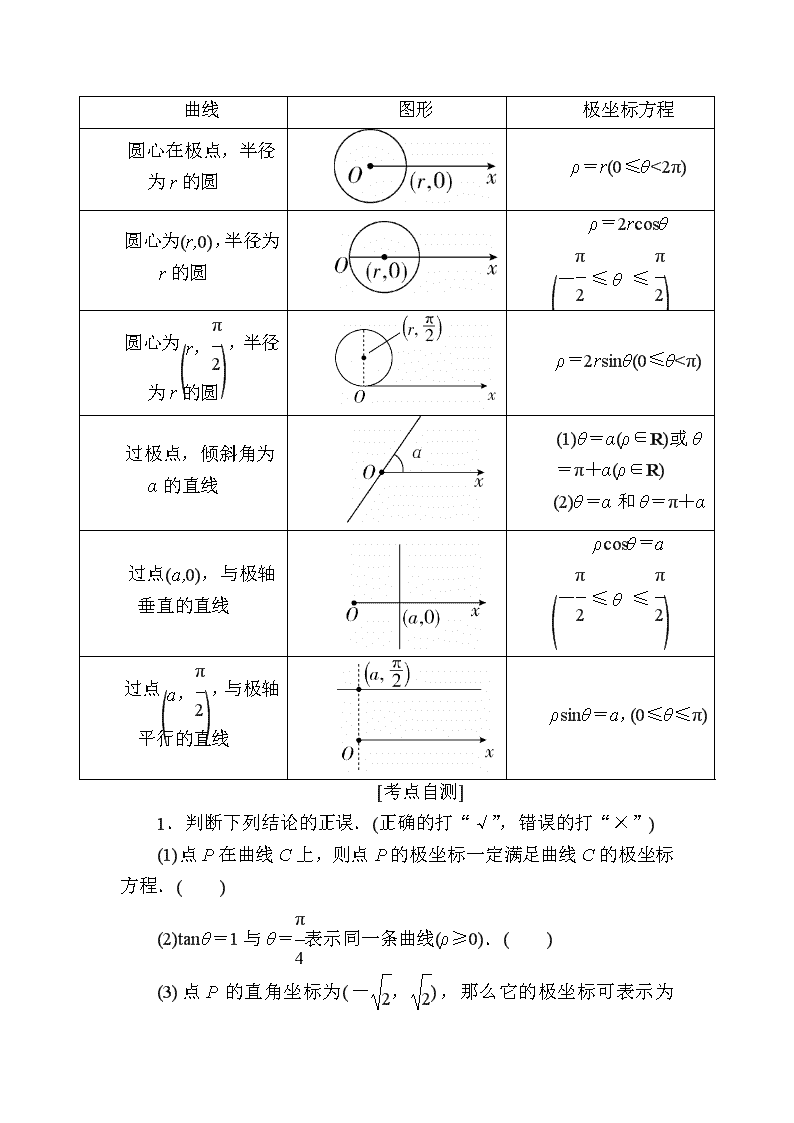考点3　常用简单曲线的极坐标方程 曲线 图形 极坐标方程 ‎ 圆心在极点，半径为r的圆 ρ＝r(0≤θ<2π)‎ 圆心为(r,0)，半径为r的圆 ρ＝2rcosθ 圆心为，半径为r的圆 ρ＝2rsinθ(0≤θ<π)‎ 过极点，倾斜角为α的直线 ‎(1)θ＝α(ρ∈R)或θ＝π＋α(ρ∈R)‎ ‎(2)θ＝α和θ＝π＋α 过点(a,0)，与极轴垂直的直线 ρcosθ＝a 过点，与极轴平行的直线 ρsinθ＝a，(0≤θ≤π)‎ ‎ [考点自测]‎ ‎1．判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)点P在曲线C上，则点P的极坐标一定满足曲线C的极坐标方程．(　　)‎ ‎(2)tanθ＝1与θ＝表示同一条曲线(ρ≥0)．(　　)‎ ‎(3)点P的直角坐标为(－，)，那么它的极坐标可表示为 ‎.(　　)‎ ‎(4)过极点，作倾斜角为α的直线的极坐标方程可表示为θ＝α或θ＝π＋α(ρ∈R)．(　　)‎ ‎(5)圆心在极轴上的点(a,0)处，且过极点O的圆的极坐标方程为ρ＝2asinθ.(　　)‎ 答案　(1)×　(2)×　(3)√　(4)√　(5)×‎ ‎2．[2018·开封模拟]方程ρ＝－2cosθ和ρ＋＝4sinθ的曲线的位置关系为(　　)‎ A．相离 B．外切 ‎ C．相交 D．内切 答案　B 解析　方程ρ＝－2cosθ化为直角坐标方程为(x＋1)2＋y2＝1，ρ＋＝4sinθ化为直角坐标方程为x2＋(y－2)2＝4，两圆圆心距为＝3＝1＋2，所以两圆外切．‎ ‎3．[2018·皖北协作区联考]在极坐标系中，直线ρ(cosθ－sinθ)＝2与圆ρ＝4sinθ的交点的极坐标为(　　)‎ A. B. C. D. 答案　A 解析　ρ(cosθ－sinθ)＝2可化为直角坐标方程x－y＝2，即y＝x－2.‎ ρ＝4sinθ可化为x2＋y2＝4y，把y＝x－2代入x2＋y2＝4y，得4x2－8x＋12＝0，即x2－2x＋3＝0，所以x＝，y＝1.所以直线与圆的交点坐标为(，1)，化为极坐标为.故选A.‎ ‎4．[2018·株洲模拟]在极坐标系中，直线ρsin(θ＋)＝2被圆ρ＝4截得的弦长为(　　)‎ A．2 B．2 ‎ C．4 D．4 答案　D 解析　直线ρsin(θ＋)＝2可化为x＋y－2＝0，圆ρ＝4可化为x2＋y2＝16，由圆中的弦长公式得2＝2＝4.‎ ‎5．[2017·北京高考]在极坐标系中，点A在圆ρ2－2ρcosθ－4ρsinθ＋4＝0上，点P的坐标为(1,0)，则|AP|的最小值为________．‎ 答案　1‎ 解析　由ρ2－2ρcosθ－4ρsinθ＋4＝0，得 x2＋y2－2x－4y＋4＝0，即(x－1)2＋(y－2)2＝1，‎ 圆心坐标为C(1,2)，半径长为1.‎ ‎∵点P的坐标为(1,0)，∴点P在圆C外．‎ 又∵点A在圆C上，∴|AP|min＝|PC|－1＝2－1＝1.‎ ‎6．[2017·天津高考]在极坐标系中，直线4ρcos＋1＝0与圆ρ＝2sinθ的公共点的个数为________．‎ 答案　2‎ 解析　由4ρcos＋1＝0得2ρcosθ＋2ρsinθ＋1＝0，故直线的直角坐标方程为2x＋2y＋1＝0.‎ 由ρ＝2sinθ得ρ2＝2ρsinθ，‎ 故圆的直角坐标方程为x2＋y2＝2y，‎ 即x2＋(y－1)2＝1.圆心为(0,1)，半径为1.‎ ‎∵圆心到直线2x＋2y＋1＝0的距离d＝＝＜1，∴‎ 直线与圆相交，有两个公共点．‎ 板块二　典例探究·考向突破 考向　平面直角坐标系下图形的变换 例　1　在平面直角坐标系中，求下列方程所对应的图形经过伸缩变换后的图形．‎ ‎(1)2x＋3y＝0；(2)x2＋y2＝1.‎ 解　由伸缩变换得到(*)．‎ ‎(1)将(*)代入2x＋3y＝0，得到经过伸缩变换后的图形方程是x′＋y′＝0.‎ 因此，经过伸缩变换后，‎ 直线2x＋3y＝0变成直线x′＋y′＝0.‎ ‎(2)将(*)代入x2＋y2＝1，得到经过伸缩变换后的图形的方程是＋＝1.‎ 因此，经过伸缩变换后，圆x2＋y2＝1变成椭圆＋＝1.‎ 触类旁通 平面直角坐标系下图形的变换技巧 平面图形的伸缩变换可以用坐标伸缩变换来表示．在伸缩变换下，直线仍然变成直线，抛物线仍然变成抛物线，双曲线仍然变成双曲线，圆可以变成椭圆，椭圆也可以变成圆．‎ ‎【变式训练1】　求椭圆＋y2＝1，经过伸缩变换后的曲线方程．‎ 解　由得到①‎ 将①代入＋y2＝1，得＋y′2＝1，即x′2＋y′2＝1.‎ 因此椭圆＋y2＝1经伸缩变换后得到的曲线方程是x2＋y2＝1.‎ 考向　极坐标与直角坐标的互化 例2　[2017·全国卷Ⅱ]在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρcosθ＝4.‎ ‎(1)M为曲线C1上的动点，点P在线段OM上，且满足|OM|·|OP|＝16，求点P的轨迹C2的直角坐标方程；‎ ‎(2)设点A的极坐标为，点B在曲线C2上，求△OAB面积的最大值．‎ 解　(1)设P的极坐标为(ρ，θ)(ρ>0)，M的极坐标为(ρ1，θ)(ρ1>0)．‎ 由题设知|OP|＝ρ，|OM|＝ρ1＝.‎ 由|OM|·|OP|＝16得C2的极坐标方程为ρ＝4cosθ(ρ>0)．‎ 因此C2的直角坐标方程为(x－2)2＋y2＝4(x≠0)．‎ ‎(2)设点B的极坐标为(ρB，α)(ρB>0)．‎ 由题设知|OA|＝2，ρB＝4cosα，于是△OAB的面积 S＝|OA|·ρB·sin∠AOB＝4cosα· ‎＝2≤2＋.‎ 当α＝－时，S取得最大值2＋.‎ 所以△OAB面积的最大值为2＋.‎ 触类旁通 直角坐标方程与极坐标方程互化的方法 直角坐标方程化为极坐标方程，只需把公式x＝ρcosθ及y＝ρsinθ 直接代入并化简即可；而极坐标方程化为直角坐标方程要通过变形，构造形如ρcosθ，ρsinθ，ρ2的形式，进行整体代换．其中方程的两边同乘以(或同除以)ρ及方程两边平方是常用的变形方法．但对方程进行变形时，方程必须保持同解，因此应注意对变形过程的检验．‎ ‎【变式训练2】　已知直线l的参数方程为(t为参数)．在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线C的方程为sinθ－ρcos2θ＝0.‎ ‎(1)求曲线C的直角坐标方程；‎ ‎(2)写出直线l与曲线C交点的一个极坐标．‎ 解　(1)∵sinθ－ρcos2θ＝0，∴ρsinθ－ρ2cos2θ＝0，‎ 即y－x2＝0.‎ ‎(2)将代入y－x2＝0得，‎ ＋t－2＝0，即t＝0，‎ 从而，交点坐标为(1，)，‎ ‎∴交点的一个极坐标为.‎ 考向　极坐标方程及其应用 例　3　[2016·全国卷Ⅱ]在直角坐标系xOy中，圆C的方程为(x＋6)2＋y2＝25.‎ ‎(1)以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；‎ ‎(2)直线l的参数方程是(t为参数)，l与C交于A，B两点，|AB|＝，求l的斜率．‎ 解　(1)由x＝ρcosθ，y＝ρsinθ，可得圆C的极坐标方程为ρ2＋12ρcosθ＋11＝0.‎ ‎(2)在(1)中建立的极坐标系中，直线l的极坐标方程为θ＝α(ρ∈R)．‎ 设A，B所对应的极径分别为ρ1，ρ2，将l的极坐标方程代入C的极坐标方程，得ρ2＋12ρcosα＋11＝0.‎ 于是ρ1＋ρ2＝－12cosα，ρ1ρ2＝11.‎ ‎|AB|＝|ρ1－ρ2|＝＝.由|AB|＝，得cos2α＝，tanα＝±.所以l的斜率为或－.‎ 触类旁通 极坐标方程及其应用的类型及解题策略 ‎(1)求极坐标方程．可在平面直角坐标系中，求出曲线方程，然后再转化为极坐标方程．‎ ‎(2)求点到直线的距离、线段的长度．先将极坐标系下点的坐标、直线、曲线方程转化为平面直角坐标系下点的坐标、直线、曲线方程，然后利用直角坐标系中点到直线的距离、线段公式求解．‎ ‎【变式训练3】　在直角坐标系xOy中，曲线C的参数方程为(α为参数)，直线l的参数方程为(t为参数)．在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，过极点O的射线与曲线C相交于不同于极点的点A，且点A的极坐标为(2，θ)，其中θ∈.‎ ‎(1)求θ的值；‎ ‎(2)若射线OA与直线l相交于点B，求|AB|的值．‎ 解　(1)由题意知，曲线C的普通方程为x2＋(y－2)2＝4，‎ ‎∵x＝ρcosθ，y＝ρsinθ，∴曲线C的极坐标方程为(ρcosθ)2＋(ρsinθ－2)2＝4，即ρ＝4sinθ.‎ 由ρ＝2，得sinθ＝，‎ ‎∵θ∈，∴θ＝.‎ ‎(2)由题易知直线l的普通方程为x＋y－4＝0，‎ ‎∴直线l的极坐标方程为ρcosθ＋ρsinθ－4＝0.‎ 又射线OA的极坐标方程为θ＝(ρ≥0)，‎ 联立，得解得ρ＝4.‎ ‎∴点B的极坐标为，‎ ‎∴|AB|＝|ρB－ρA|＝4－2＝2.‎ 核心规律 如何解决极坐标问题 ‎(1)解决极坐标系中的一些问题时，主要的思路是将极坐标化为直角坐标，在直角坐标系下求解后，再转化为极坐标．‎ ‎(2)极坐标方程与直角坐标方程互化的核心公式：‎ ⇒ ‎(3)由极坐标系上点的对称性可得到极坐标方程ρ＝ρ(θ)的图形的对称性：若ρ(θ)＝ρ(－θ)，则相应图形关于极轴对称；若ρ(θ)＝ρ(π－θ)，则图形关于射线θ＝所在的直线对称；若ρ(θ)＝ρ(π＋θ)，则图形关于极点O对称．‎ 满分策略 极坐标应用中的注意事项 ‎(1)极坐标与直角坐标互化的前提条件：①极点与原点重合；②极轴与x轴正方向重合；③取相同的长度单位．‎ ‎(2)若把直角坐标化为极坐标，求极角θ时，应注意判断点P所在的象限(即角θ的终边的位置)，以便正确地求出角θ.利用两种坐标的互化，可以把不熟悉的问题转化为熟悉的问题．‎ ‎(3)‎ 由极坐标的意义可知平面上点的极坐标不是唯一的，如果限定ρ取正值，θ∈[0,2π)，平面上的点(除去极点)与极坐标(ρ，θ)(ρ≠0)建立一一对应关系.‎ 板块三　模拟演练·提能增分 ‎ [基础能力达标]‎ ‎1．[2018·广东珠海模拟]在极坐标系中，圆C的极坐标方程为ρ2＝4ρ(cosθ＋sinθ)－6.若以极点O为原点，极轴所在直线为x轴建立平面直角坐标系．‎ ‎(1)求圆C的参数方程；‎ ‎(2)在直角坐标系中，点P(x，y)是圆C上一动点，试求x＋y的最大值，并求出此时点P的直角坐标．‎ 解　(1)因为ρ2＝4ρ(cosθ＋sinθ)－6，‎ 所以x2＋y2＝4x＋4y－6，‎ 所以x2＋y2－4x－4y＋6＝0，‎ 整理得(x－2)2＋(y－2)2＝2.‎ 所以圆C的参数方程为(θ为参数)．‎ ‎(2)由(1)可得x＋y＝4＋(sinθ＋cosθ)＝4＋2sin.‎ 当θ＝，即点P的直角坐标为(3,3)时，x＋y取得最大值，其值为6.‎ ‎2．[2018·宁波模拟]已知曲线C1的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sinθ.‎ ‎(1)把C1的参数方程化为极坐标方程；‎ ‎(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)．‎ 解　(1)将消去参数t，‎ 化为普通方程(x－4)2＋(y－5)2＝25，即C1：x2＋y2－8x－10y＋16＝0.‎ 将代入x2＋y2－8x－10y＋16＝0得ρ2－8ρcosθ－10ρsinθ＋16＝0.‎ 所以C1的极坐标方程为ρ2－8ρcosθ－10ρsinθ＋16＝0.‎ ‎(2)C2的直角坐标方程为x2＋y2－2y＝0.‎ 由 解得或 所以C1与C2交点的极坐标分别为，.‎ ‎3．[2018·南通模拟]在直角坐标系xOy中，圆C的参数方程为(φ为参数)．以O为极点，x轴的非负半轴为极轴建立极坐标系．‎ ‎(1)求圆C的普通方程；‎ ‎(2)直线l的极坐标方程是2ρsin＝5，射线OM：θ＝与圆C的交点为O，P，与直线l的交点为Q，求线段PQ的长．‎ 解　(1)因为圆C的参数方程为(φ为参数)，所以圆心C的坐标为(0,2)，半径为2，圆C的普通方程为x2＋(y－2)2＝4.‎ ‎(2)将x＝ρcosθ，y＝ρsinθ代入x2＋(y－2)2＝4，得圆C的极坐标方程为ρ＝4sinθ.‎ 设P(ρ1，θ1)，则由解得ρ1＝2，θ1＝.‎ 设Q(ρ2，θ2)，则由 解得ρ2＝5，θ2＝.所以|PQ|＝3.‎ ‎4．[2018·昆明模拟]将圆x2＋y2＝1上每一点的横坐标变为原来的2倍，纵坐标变为原来的3倍，得曲线Γ.‎ ‎(1)写出Γ的参数方程；‎ ‎(2)设直线l：3x＋2y－6＝0与Γ的交点为P1，P2‎ ‎，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求过线段P1P2的中点且与l垂直的直线的极坐标方程．‎ 解　(1)设(x1，y1)为圆上的点，在已知变换下变为Γ上的点(x，y)，依题意，得即 由x＋y＝1，得2＋2＝1，即曲线Γ的方程为＋＝1.‎ 故Γ的参数方程为(t为参数)．‎ ‎(2)由解得或 不妨设P1(2,0)，P2(0,3)，则线段P1P2的中点坐标为，所求直线的斜率k＝.于是所求直线方程为y－＝(x－1)，即4x－6y＋5＝0，化为极坐标方程，得4ρcosθ－6ρsinθ＋5＝0.‎ ‎5．[2016·全国卷Ⅲ]在直角坐标系xOy中，曲线C1的参数方程为(α为参数)．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为ρsin＝2.‎ ‎(1)写出C1的普通方程和C2的直角坐标方程；‎ ‎(2)设点P在C1上，点Q在C2上，求|PQ|的最小值及此时P的直角坐标．‎ 解　(1)由曲线C1：得即曲线C1的直角坐标方程为＋y2＝1.‎ 由曲线C2：ρsin＝2，得ρ(sinθ＋cosθ)＝2，即曲线C2的直角坐标方程为x＋y－4＝0.‎ ‎(2)由题意，可设点P的直角坐标为(cosα，sinα)．因为C2是直线，所以|PQ|的最小值即为P到C2的距离d(α)的最小值，‎ d(α)＝＝.‎ 当且仅当α＝2kπ＋(k∈Z)时，d(α)取得最小值，最小值为，此时P的直角坐标为.‎ ‎6．[2018·合肥模拟]在直角坐标系xOy中，曲线C1的参数方程为(其中φ为参数)，曲线C2：x2＋y2－2y＝0，以原点O为极点，x轴的正半轴为极轴建立极坐标系，射线l：θ＝α(ρ≥0)与曲线C1，C2分别交于点A，B(均异于原点O) .‎ ‎(1)求曲线C1，C2的极坐标方程；‎ ‎(2)当0<α<时，求|OA|2＋|OB|2的取值范围．‎ 解　(1)∵(φ为参数)，∴＋y2＝1.‎ 由得曲线C1的极坐标方程为ρ2＝.‎ ‎∵x2＋y2－2y＝0，∴曲线C2的极坐标方程为ρ＝2sinθ.‎ ‎(2)由(1)得|OA|2＝ρ2＝，|OB|2＝ρ2＝4sin2α，‎ ‎∴|OA|2＋|OB|2＝＋4sin2α＝＋4(1＋sin2α)－4，‎ ‎∵0<α<，∴1<1＋sin2α<2，∴6<＋4(1＋sin2α)<9，‎ ‎∴|OA|2＋|OB|2的取值范围为(2,5)．‎