高中数学人教a版选修4-1课后习题解答：2-5与圆有关的比例线段 4页

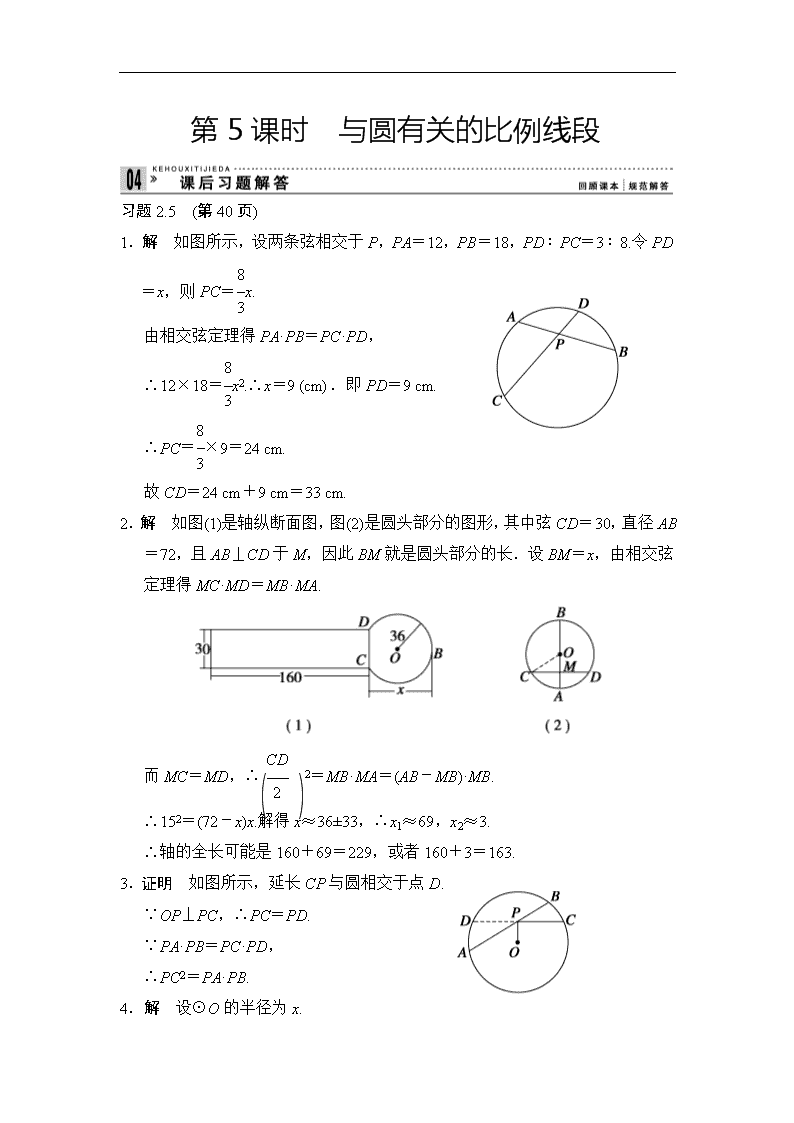
第5课时　与圆有关的比例线段 习题2.5　(第40页)‎ ‎1．解　如图所示，设两条弦相交于P，PA＝12，PB＝18，PD∶PC＝3∶8.令PD＝x，则PC＝x.‎ 由相交弦定理得PA·PB＝PC·PD，‎ ‎∴12×18＝x2.∴x＝9 (cm)．即PD＝‎9 cm.‎ ‎∴PC＝×9＝‎24 cm.‎ 故CD＝‎24 cm＋‎9 cm＝‎33 cm.‎ ‎2．解　如图(1)是轴纵断面图，图(2)是圆头部分的图形，其中弦CD＝30，直径AB＝72，且AB⊥CD于M，因此BM就是圆头部分的长．设BM＝x，由相交弦定理得MC·MD＝MB·MA.‎ 而MC＝MD，∴2＝MB·MA＝(AB－MB)·MB.‎ ‎∴152＝(72－x)x.解得x≈36±33，∴x1≈69，x2≈3.‎ ‎∴轴的全长可能是160＋69＝229，或者160＋3＝163.‎ ‎3．证明　如图所示，延长CP与圆相交于点D.‎ ‎∵OP⊥PC，∴PC＝PD.‎ ‎∵PA·PB＝PC·PD，‎ ‎∴PC2＝PA·PB.‎ ‎4．解　设⊙O的半径为x.‎ ‎∵PO＝PC＋x，∴PC＝PO－x＝12－x.‎ 又PB＝PA＋AB＝6＋7＝.‎ ‎∵PA·PB＝PC·PD，‎ ‎∴6×＝(12－x)(12＋x)．‎ 解得x＝8.‎ ‎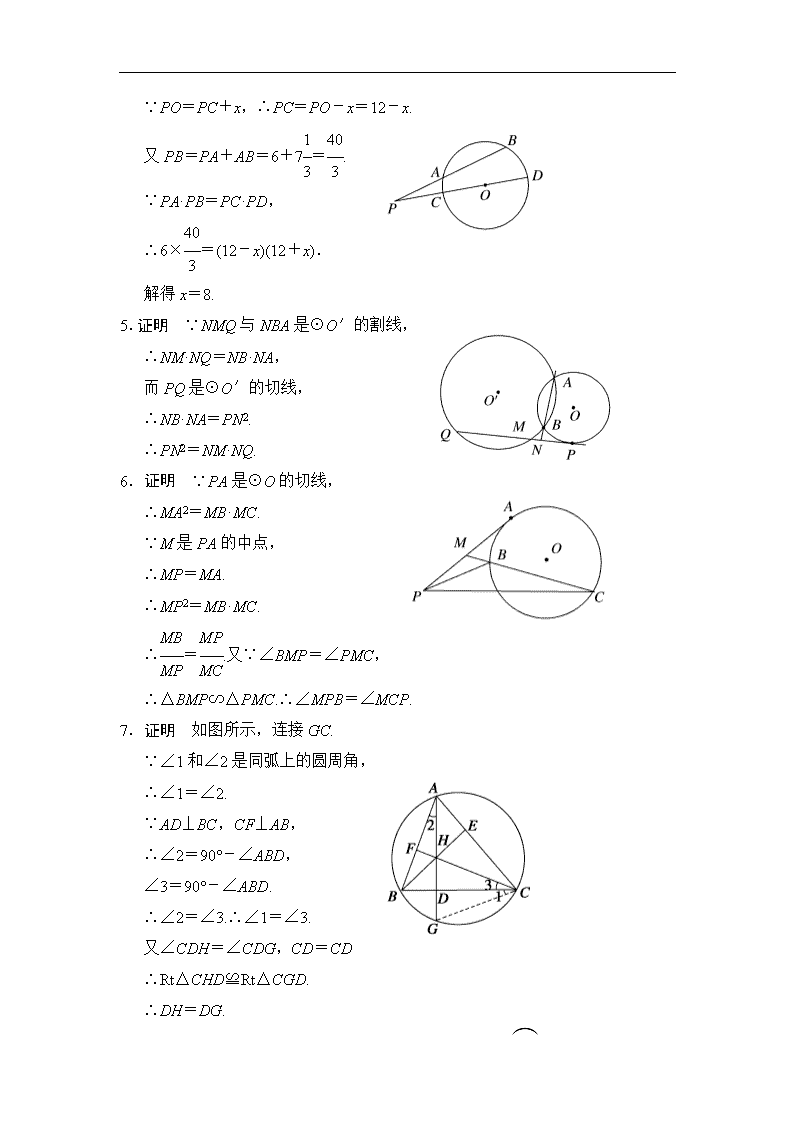5．证明　∵NMQ与NBA是⊙O′的割线，‎ ‎∴NM·NQ＝NB·NA，‎ 而PQ是⊙O′的切线，‎ ‎∴NB·NA＝PN2.‎ ‎∴PN2＝NM·NQ.‎ ‎6．证明　∵PA是⊙O的切线，‎ ‎∴MA2＝MB·MC.‎ ‎∵M是PA的中点，‎ ‎∴MP＝MA.‎ ‎∴MP2＝MB·MC.‎ ‎∴＝.又∵∠BMP＝∠PMC，‎ ‎∴△BMP∽△PMC.∴∠MPB＝∠MCP.‎ ‎7．证明　如图所示，连接GC.‎ ‎∵∠1和∠2是同弧上的圆周角，‎ ‎∴∠1＝∠2.‎ ‎∵AD⊥BC，CF⊥AB，‎ ‎∴∠2＝90°－∠ABD，‎ ‎∠3＝90°－∠ABD.‎ ‎∴∠2＝∠3.∴∠1＝∠3.‎ 又∠CDH＝∠CDG，CD＝CD ‎∴Rt△CHD≌Rt△CGD.‎ ‎∴DH＝DG.‎ ‎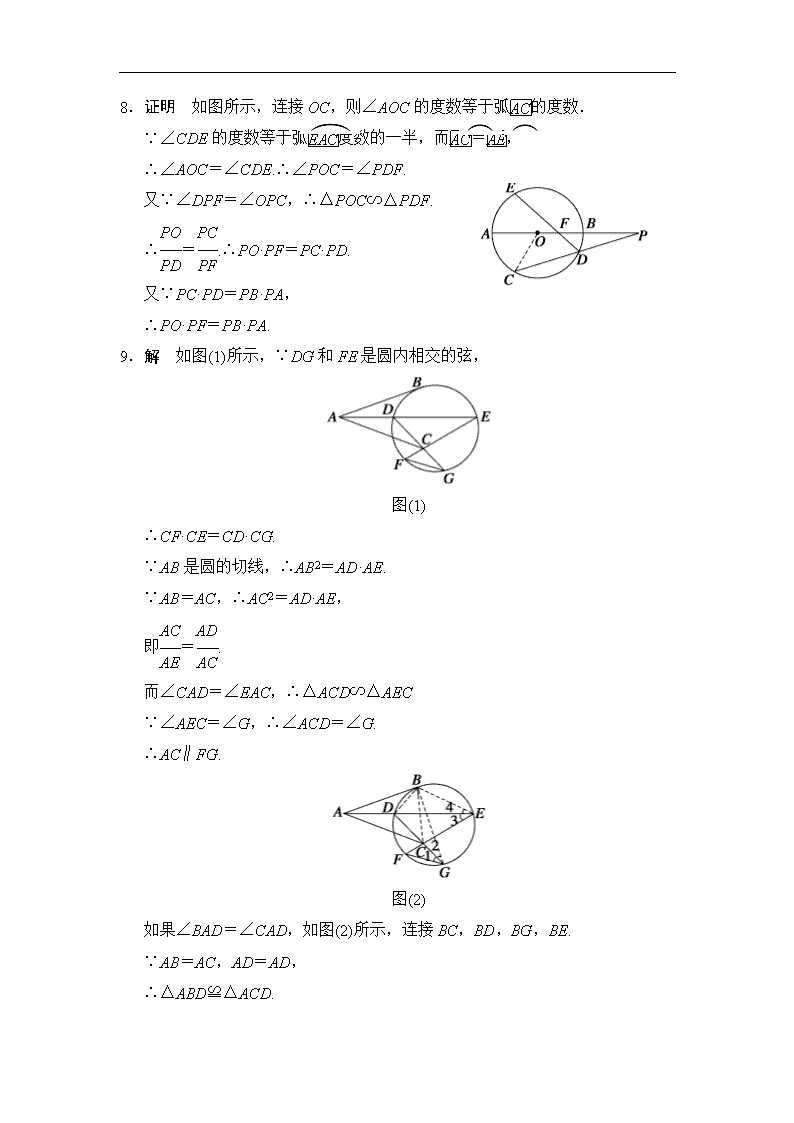8．证明　如图所示，连接OC，则∠AOC的度数等于弧的度数．‎ ‎∵∠CDE的度数等于弧度数的一半，而＝，‎ ‎∴∠AOC＝∠CDE.∴∠POC＝∠PDF.‎ 又∵∠DPF＝∠OPC，∴△POC∽△PDF.‎ ‎∴＝.∴PO·PF＝PC·PD. ‎ 又∵PC·PD＝PB·PA，‎ ‎∴PO·PF＝PB·PA.‎ ‎9．解　如图(1)所示，∵DG和FE是圆内相交的弦，‎ 图(1)‎ ‎∴CF·CE＝CD·CG.‎ ‎∵AB是圆的切线，∴AB2＝AD·AE.‎ ‎∵AB＝AC，∴AC2＝AD·AE，‎ 即＝.‎ 而∠CAD＝∠EAC，∴△ACD∽△AEC ‎∵∠AEC＝∠G，∴∠ACD＝∠G.‎ ‎∴AC∥FG.‎ 图(2)‎ 如果∠BAD＝∠CAD，如图(2)所示，连接BC，BD，BG，BE.‎ ‎∵AB＝AC，AD＝AD，‎ ‎∴△ABD≌△ACD.‎ ‎∴BD＝CD.‎ ‎∠ABD＝∠ACD.‎ ‎∵∠ACD＝∠1，∠ABD＝∠2，‎ ‎∴∠1＝∠2.‎ ‎∴＝，∴∠3＝∠4.‎ ‎∴△ABE≌△ACE.‎ ‎∴BE＝CE.∵AB＝AC，∠BAD＝∠CAD，‎ ‎∴AE⊥BC.‎ ‎∴四边形ABEC各边的中点在同一个圆周上．‎ ‎∵AB＝AC，EB＝EC，∴AB＋EC＝AC＋EB.①‎ 由①可以推出，四边形ABEC存在内切圆(证明略)．‎