高中数学选修2-2课件数学归纳法（一） 10页

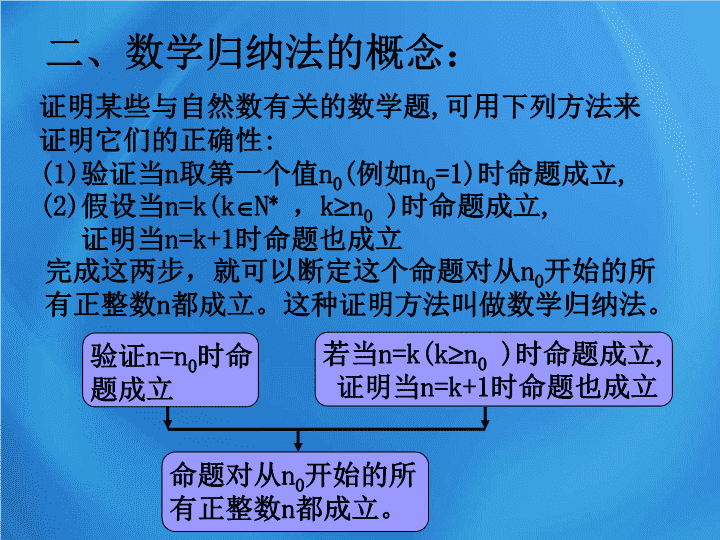
2.3 数学归纳法 (1) 对于某类事物，由它的一些特殊事例或其全部可能情况，归纳出一般结论的推理方法，叫归纳法。 归纳法 ｛ 完全归纳法 不完全归纳法 由特殊 一般 特点 : a 2 =a 1 +d a 3 =a 1 +2d a 4 =a 1 +3d …… a n =a 1 +(n-1)d 如何证明 :1+3+5+…+(2n-1)=n 2 (n∈N*) 二、数学归纳法的概念： 证明某些与自然数有关的数学题 , 可用下列方法来证明它们的正确性 : (1) 验证 当 n 取第一个值 n 0 ( 例如 n 0 =1) 时命题成立 , (2) 假设 当 n=k(k N * ， kn 0 ) 时命题成立 , 证明当 n=k+1 时命题也成立 完成这两步，就可以断定这个命题对从 n 0 开始的所有正整数 n 都成立。这种证明方法叫做 数学归纳法。 验证 n=n 0 时命题成立 若 当 n=k( kn 0 ) 时命题成立 , 证明当 n=k+1 时命题也成立 命题对从 n 0 开始的所有正整数 n 都成立。 所以 n=k+1 时结论也成立 那么 求证 注意 1 . 用数学归纳法进行证明时 , 要分两个步骤 , 两个步骤缺一不可 . 2 (1)( 归纳奠基 ) 是递推的基础 . 找准 n 0 (2)( 归纳递推 ) 是递推的依据　　　 n ＝ k 时命题成立．作为必用的条件运用，而 n ＝ k+1 时情况则有待 利用假设 及已知的定义、公式、定理等加以证明  证明：①当 n=1 时，左边 =1 ，右边 =1 ，等式成立。 ②假设 n=k(k∈N ,k≥1) 时等式成立 , 即： 1+3+5+ …… +(2k-1)=k 2 ， 当 n=k+1 时： 1+3+5+ …… +(2k-1)+[2(k+1)-1]=k 2 +2k+1=(k+1) 2 ， 所以当 n=k+1 时等式也成立。 由①和②可知，对 n∈N ，原等式都成立。  例、用数学归纳法证明 1+3+5+ …… +(2n-1)=n 2 （ n∈N ） .  请问： 第②步中 “ 当 n=k+1 时 ” 的证明可否改换为： 1+3+5+ …… +(2k-1)+[2(k+1)-1]= 1+3+5+ …… +(2k-1)+(2k+1) = = (k+1) 2 ? 为什么？  例 : 用数学归纳法证明 注意 1 . 用数学归纳法进行证明时 , 要分两个步骤 , 两个步骤缺一不可 . 2 (1)( 归纳奠基 ) 是递推的基础 . 找准 n 0 (2)( 归纳递推 ) 是递推的依据　　　 n ＝ k 时命题成立．作为必用的条件运用，而 n ＝ k+1 时情况则有待 利用假设 及已知的定义、公式、定理等加以证明 例、求证 : ( n+1)(n+2) … (n+n)=2 n • 1 • 3 •… • (2n-1) 证明：① n=1 时：左边 =1+1=2 ，右边 =2 1 • 1=2 ，左边 = 右边，等 式成立。 ② 假设当 n=k((k∈N ）时有： (k+1)(k+2) … (k+k)=2 k • 1 • 3 •…• (2n-1), 当 n=k+1 时： 左边 =(k+2)(k+3) … (k+k)(k+k+1)(k+k+2) =(k+1)(k+2)(k+3) … (k+k) • = 2 k • 1 • 3 •…• (2k-1)(2k+1) • 2 = 2 k+1 • 1 • 3 •…• (2k-1) • [2(k+1)-1]= 右边， ∴当 n=k+1 时等式也成立。 由 ①、②可知，对一切 n∈N , 原等式均成立。   作业 :P 108 A 组 1 (2) B 组 3 谢谢合作！