- 1.35 MB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2.3.2
抛物线
的简单几何性质
(1)
一、温故知新
(
一
)
圆锥曲线的统一定义
平面内,到定点
F
的距离与到定直线
l
的距离比为常数
e
的点的轨迹
,
当
e
>
1
时,是
双曲线
.
当
0
0)
(2)
开口向左
y
2
= -2px (p
>
0)
(3)
开口向上
x
2
= 2py (p
>
0)
(4)
开口向下
x
2
= -2py (p
>
0)
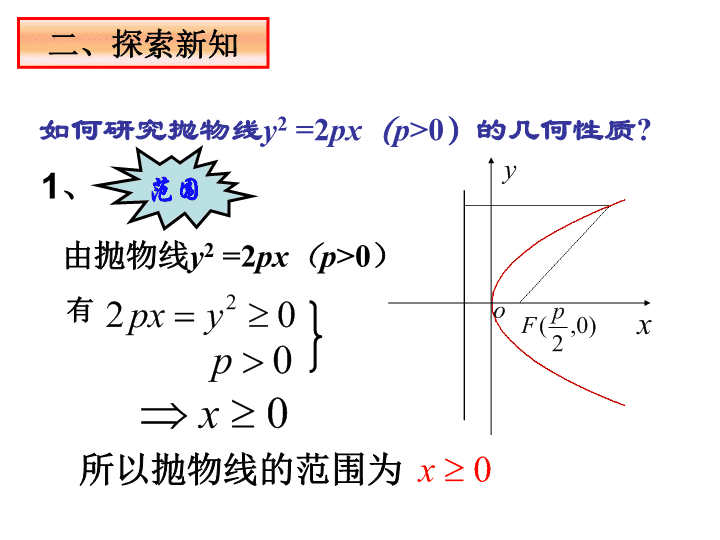
范围
1
、
由抛物线
y
2
=2
px
(
p
>0
)
有
所以抛物线的范围为
二、探索新知
如何研究抛物线
y
2
=2
px
(
p
>0
)的几何性质
?
对称性
2
、
关于
x
轴
对称
即点
(x,-y)
也在抛物线上
,
故 抛物线
y
2
= 2
px(p
>0)
关于
x
轴
对称
.
则
(-y
)
2
= 2
px
若点
(x,y
)
在抛物线上
,
即满足
y
2
= 2
px
,
顶点
3
、
定义:抛物线与它的对称轴的交点叫做抛物线的
顶点
。
y
2
= 2
px
(
p
>0)
中,
令
y=0,
则
x=0.
即:抛物线
y
2
= 2
px
(
p
>0)
的
顶点(
0
,
0
)
.
离心率
4
、
P(x,y)
抛物线上的点与焦点的距离和它到准线的距离之比,叫做
抛物线的
离心率
。
由定义知, 抛物线
y
2
= 2
px
(
p
>0)
的离心率为
e=1
.
x
y
O
F
A
B
y
2
=2
px
2
p
过焦点而垂直于对称轴的弦
AB
,称为抛物线的
通径,
利用抛物线的
顶点
、通径的两个
端点
可较准确画出反映抛物线基本特征的草图
.
|AB|=2
p
通径
5
、
2
p
越大,抛物线张口越大
.
连接抛物线任意一点与焦点的线段叫做抛物线的
焦半径
。
|PF|=x
0
+p/2
焦半径公式:
焦半径
6
、
x
y
O
F
P
通过焦点的直线,与抛物
线相交于两点,连接这两点的
线段叫做抛物线的
焦点弦
。
x
O
y
F
A
焦点弦公式:
下面请大家推导出其余三种标准方程抛物线的
焦点弦公式。
B
焦点弦
7
、
方程
图
形
范围
对称性
顶点
焦半径
焦点弦的长度
y
2
= 2
px
(
p
>
0
)
y
2
= -2
px
(
p
>
0
)
x
2
= 2
py
(
p
>
0
)
x
2
= -2
py
(
p
>
0
)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x
≥0
y
∈R
x
≤0
y
∈R
x
∈R
y
≥0
y
≤0
x
∈R
l
F
y
x
O
关于
x
轴对称
关于
x
轴对称
关于
y
轴对称
关于
y
轴对称
(
0,0
)
(
0,0
)
(
0,0
)
(
0,0
)
归纳
:
(1)
、抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但
没有渐近线
;
(2)
、抛物线只有一条对称轴
,
没有对称中心
;
(3)
、抛物线
只有一个顶点,一个焦点,一条准线;
(4)
、抛物线的离心率
e
是确定的为1
,
⑸
、抛物线的通径为
2P,
2p
越大,抛物线的张口越大
.
探照灯、汽车前灯的反光曲面,手电筒的反光镜面、太阳灶的镜面都是
抛物镜面。
抛物镜面:
抛物线绕其对称轴旋转而成的曲面。
灯泡放在抛物线的
焦点
位置上,通过镜面反射就变
成了
平行光束
,这就是探照灯、汽车前灯、手电筒的
设计原理。
平行光线射到抛物镜面上,经镜面反射后,
反射光线都
经过抛物线的焦点,
这就是太阳灶能把光能转化为热能
的理论依据。
三、典例精析
1
、
2---
抛物线的光学性质
例
2
:探照灯反射镜的轴截面是抛物线的一部分,光源
位于抛物线的焦点处。已知灯口圆的直径为
60
cm
,灯深
40
cm
,求抛物线的标准方程和焦点位置。
课本
70
页例
3
x
y
O
(40,30)
解
:
所在平面内建立直
角坐标系
,
使反射镜
的顶点与原点重合
,
x
轴垂直于灯口直径
.
在探照灯的轴截面
设抛物线的标准方程为
:
y
2
=2
px
由条件可得
A (40,30),
代入方程得
:
30
2
=2
p·
40
解之
:
p=
故所求抛物线的标准方程为
:
y
2
=
x,
焦点为
( ,0)
例题
3
解读例
19
课本
63
页例
3
变形
三、典例精析
3--
桥孔问题
解读例
19
课本
63
页例
3
三、典例精析
4—
彗星的运行轨道
(
1
)已知点
A
(
-2
,
3
)与抛物线
的焦点的距离是
5
,则
P
=
。
(
2
)抛物线 的弦
AB
垂直
x
轴,若
|AB|=
,
则焦点到
AB
的距离为
。
4
2
(
3
)已知直线
x
-
y
=2
与抛物线 交于
A
、
B
两
点,那么线段
AB
的中点坐标是
。
四、课堂练习(备选)
5.
点
A
的坐标为
(3
,
1)
,若
P
是抛物线 上的一动点,
F
是抛物线的焦点,则
|
PA
|+|
P
F|
的最小值为
(
)
(
A
) 3 (B) 4 (C) 5 (D) 6
4
、求满足下列条件的抛物线的标准方程:
(1)
焦点在直线
x-2y-4=0
上
.
(2)
焦点在轴
x
上且截直线
2x-y+1=0
所得的弦长为
6
、已知
Q(4,0)
,
P
为抛物线 上任一点,则
|PQ|
的最小值为
( )
A. B. C. D.
B
C
五、归纳总结
抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
抛物线只有一条对称轴
,
没有对称中心
;
抛物线的离心率是确定的,等于1;
抛物线只有一个顶点,一个焦点,一条准线;
抛物线的通径为
2P, 2p
越大,抛物线的张口越大
.
1
、范围:
2
、对称性:
3
、顶点:
4
、离心率:
5
、通径:
6
、光学性质:
从焦点出发的光线,通过抛物线反射就变成了平行光束
.