高中数学选修2-2课件3_1_2 49页

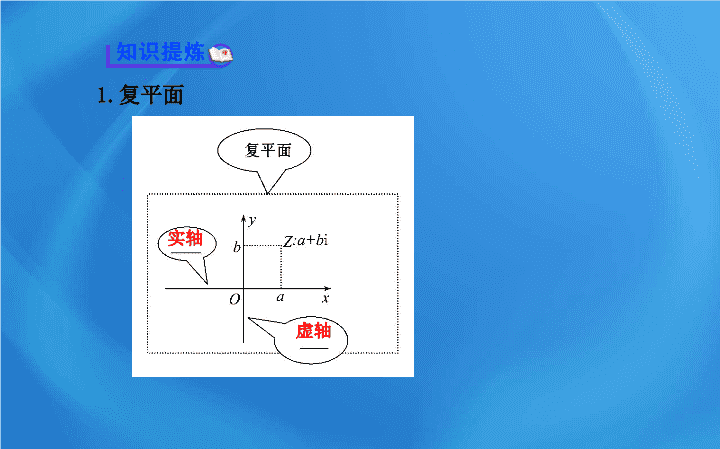
3.1.2 　 复数的几何意义 问题 引航 1. 复平面是如何定义的 , 复数的模如何求出 ? 2. 复数与复平面内的点及向量的关系如何 ? 复数的模是实数还是复数 ? 1. 复平面 实轴 虚轴 2. 复数的几何意义 (1) 复数 z=a+bi(a,b∈R) ___________________. (2) 复数 z=a+bi(a,b∈R) ________________________. 3. 复数的模 (1) 定义 : 向量 的 ___r 叫做复数 z=a+bi(a,b∈R) 的模 . (2) 记法 : 复数 z=a+bi 的模记为 ____________. (3) 公式 :|z|=|a+bi|=r=_________(r≥0,r∈R). 复平面内的点 Z(a,b) 平面向量 (O 为坐标原点 ) 模 |z| 或 |a+bi| 1. 判一判 ( 正确的打 “ √ ” , 错误的打 “ × ” ) (1) 在复平面内 , 对应于实数的点都在实轴上 . 　 ( 　　 ) (2) 在复平面内 , 虚轴上的点所对应的复数都是纯虚数 . 　 ( 　　 ) (3) 复数的模一定是正实数 . 　 ( 　　 ) 【 解析 】 (1) 正确 , 根据实轴的定义 ,x 轴叫实轴 , 实轴上的点都表示实数 , 反过来 , 实数对应的点都在实轴上 , 如实轴上的点 (2,0) 表示实数 2. (2) 错误 , 根据虚轴的定义 ,y 轴叫虚轴 , 而原点对应的有序实数对为 (0,0), 它所确定的复数是 z=0+0i=0 表示的是实数 , 故除了原点外 , 虚轴上的点都表示纯虚数 . (3) 错误 , 复数的模一定是实数但不一定是正实数 , 如 :0 也是复数 , 它的模为 0 不是正实数 . 答案 : (1)√ 　 (2)× 　 (3)× 2 ．做一做 ( 请把正确的答案写在横线上 ) (1) 若 ＝ (0 ，－ 3) ，则 对应的复数为 _________. (2) 复数 z=1-4i 位于复平面上的第 ______ 象限 . (3) 复数 的模是 ________. 【 解析 】 (1) 由 ＝ (0 ，－ 3) ，得点 Z 的坐标为 (0 ，－ 3) ， 所以对应的复数为 0 － 3i ＝－ 3i. 答案： -3i (2) 因为复数 z=1-4i 对应的点为 (1,-4) ，所以 z=1-4i 位于 复平面上的第四象限 . 答案： 四 (3) 复数 i 的模是 答案： 【 要点探究 】 知识点 1 复数的几何意义 1. 复平面、实轴、虚轴与复数的对应 (1) 复平面内点的坐标与复数实部虚部的对应 : 点 Z 的横坐标是 a, 纵坐标是 b, 复数 z=a+bi(a,b∈R) 可用点 Z(a,b) 表示 . (2) 实轴与复数的对应 : 实轴上的点都表示实数 . (3) 虚轴与复数的对应 : 除了原点外 , 虚轴上的点都表示纯虚数 , 原点对应的有序实数对为 (0,0), 它所确定的复数是 z=0+0i=0, 表示的是实数 . (4) 象限内的点与复数的对应 : ① 第一象限的复数特点 : 实部为正 , 且虚部为正 ; ② 第二象限的复数特点 : 实部为负 , 且虚部为正 ; ③ 第三象限的复数特点 : 实部为负 , 且虚部为负 ; ④ 第四象限的复数特点 : 实部为正 , 且虚部为负 . 2. 复数的几何意义的两个注意点 (1) 复数与复平面上的点：复数 z ＝ a ＋ bi(a ， b∈R) 的对应点的 坐标为 (a ， b) ，而不是 (a ， bi). (2) 复数与向量的对应：复数 z ＝ a ＋ bi(a ， b∈R) 的对应向量 是以原点 O 为起点的，否则就谈不上一一对应，因为复平面 上与 相等的向量有无数个． 【 知识拓展 】 复平面上的点与复数一一对应 (1) 复数 z=a+bi(a,b∈R) 与有序实数对 (a,b) 是一一对应关系 , 这是因为对于任何一个复数 z=a+bi(a,b∈R) 由复数相等的定义可知 , 可以由一个有序实数对 (a,b) 唯一确定 , 如 z=3+2i 可以由有序实数对 (3,2) 确定 . (2) 有序实数对 (a,b) 与平面直角坐标系中的点是一一对应的 , 如有序实数对 (3,2), 它与平面直角坐标系中横坐标为 3, 纵坐标为 2 的点 A, 建立了一一对应的关系 . 【 微思考 】 (1) 原点 O 在虚轴上 , 则数 0 是否也可以看作为虚数 ? 提示 : 不可以 . 数 0 为实数 , 不是虚数 . (2) 实数可用数轴上的点来表示 , 类比一下 , 复数怎样来表示呢 ? 提示 : 任何一个复数 z=a+bi(a,b∈R), 都和一个有序实数对 (a,b) 一一对应 , 因此 , 复数集与平面直角坐标系中的点集一一对应 . 【 即时练 】 下列有关复数概念的说法中正确的个数是　 ( 　　 ) ① 复数 a+bi(a,b∈R) 的实部为 a, 虚部是 b; ② 两个虚数只能说相等或不相等 , 而不能比较大小 ; ③ 复平面上 , 实轴上的点都表示实数 ; ④ 复数集 C 和复平面内所有的点构成的集合是一一对应的 . A.1 　　　　 B.2 　　　　 C.3 　　　　 D.4 【 解析 】 选 D.① 复数 a+bi(a,b∈R) 的实部为 a, 虚部是 b, 满足复数的定义 , 正确 ; ② 两个虚数只能说相等或不相等 , 而不能比较大小 , 只有两个复数是实数时 , 才能比较大小 , 正确 ; ③ 复平面上 , 实轴上的点都表示实数 , 满足复平面的基本性质 , 正确 ; ④ 复数集 C 和复平面内所有的点构成的集合是一一对应的 . 满足复数与复平面的点的对应关系 , 正确 . 知识点 2 复数的模 对复数模的三点说明 (1) 数的角度理解 : 复数 a+bi(a,b∈R) 的模 |a+bi|= 两个虚数不能比较大小 , 但它们的模可以比较大小 . (2) 几何角度理解 : 表示复数的点 Z 到原点的距离 .|z 1 -z 2 | 表示 复数 z 1 ,z 2 对应的点之间的距离 . (3) 特殊情形 : 如果 b=0, 那么 z=a+bi(a,b∈R) 是一个实数 a, 它 的模等于 |a|( 就是 a 的绝对值 ). 【 微思考 】 (1) 复数的模可以等于该复数吗 ? 提示 : 可以 , 当复数为正实数时就可以 . (2) 任意两个复数的模能比较大小吗 ? 提示 : 复数的模为实数 , 故能比较大小 . 【 即时练 】 已知复数 z 的实部为－ 1 ，虚部为 2 ，则｜ z ｜ =( ) 【 解析 】 选 A. 由模的定义得 【 题型示范 】 类型一 复数与复平面内点的关系 【 典例 1】 (1)(2014· 重庆高考 ) 实部为 -2, 虚部为 1 的复数所对应的点位于复平面的 ( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 (2) 在复平面内 , 若复数 z=(m 2 -m-2)+(m 2 -3m+2)i(m∈R) 的对应点 ①在虚轴上 ; ② 在实轴负半轴上 , 分别求复数 z. 【 解题探究 】 1. 题 (1) 中复数对应的点是什么？ 2. 题 (2) 中复数 z=(m 2 -m-2)+(m 2 -3m+2)i 对应点的坐标是多少 ? 【 探究提示 】 1. 是 (-2,1). 2. 复数 z=(m 2 -m-2)+(m 2 -3m+2)i 对应点的坐标是 (m 2 -m-2,m 2 -3m+2). 【 自主解答 】 (1) 选 B. 实部为 -2, 虚部为 1 的复数所对应的复 平面内的点为 (-2,1) ，位于第二象限 , 故选 B. (2)① 若复数 z 对应点在虚轴上，则 m 2 － m － 2 ＝ 0 ， 所以 m ＝－ 1 ，或 m ＝ 2 ，此时， z ＝ 6i ，或 z ＝ 0. ② 若复数 z 对应点在实轴负半轴上，则 解得 m ＝ 1 ，所以 z ＝－ 2. 【 方法技巧 】 利用复数 与点的对应解题的步骤 (1) 找对应关系 : 复数的几何表示法即复数 z=a+bi(a,b∈R) 可以用复平面内的点 Z(a,b) 来表示 , 是解决此类问题的根据 . (2) 列出方程 : 此类问题可建立复数的实部与虚部应满足的条件 , 通过解方程 ( 组 ) 或不等式 ( 组 ) 求解 . 【 变式训练 】 已知复数 x 2 -6x+5+(x-2)i 在复平面内对应的点在 第二象限 , 求实数 x 的取值范围 . 【 解题指南 】 根据复数在复平面内对应点所在的象限 , 确定实 部和虚部对应的不等式 , 由不等式组求出 x 的范围 . 【 解析 】 复数 x 2 － 6x ＋ 5 ＋ (x － 2)i 在复平面内对应的点的坐标 为 (x 2 － 6x ＋ 5 ， x － 2) ，因在第二象限，所以有 故实数 x 的取值范围是 22 的解集是圆 |z| ＝ 2 外部所有的点组成的集合， 这两个集合的交集就是不等式组 所表示的集合．容易看出，点 Z 的集合是以原点 O 为圆心，以 2 及 4 为半径的圆所夹的圆环，但不包括圆环的边界． 【 补偿训练 】 设复数 z 的模为 17 ，虚部为－ 8 ，则复数 z ＝ _____. 【 解析 】 设复数 z=a-8i(a∈R) ，由 所以 a 2 =225,a=±15 ， z=±15 － 8i. 答案： ±15 － 8i 类型三 复数与复平面内向量的关系 【 典例 3】 (1) 设 O 是原点，向量 对应的复数分别为 2 － 3i, － 3+2i ，那么向量 对应的复数是 ( ) A. － 5+5i B. － 5 － 5i C.5+5i D.5 － 5i (2)(2014· 黄山高二检测 ) 在复平面内， O 是原点，向量 对应的复数为 2+i. ① 如果点 A 关于实轴的对称点为点 B ，求向量 对应的复数； ②如果①中的点 B 关于虚轴的对称点为点 C ，求点 C 对应的复数 . 【 解题探究 】 1. 题 (1) 中向量 对应复平面内点的坐标是多少，若知道 A(x 1 ,y 1 ) ， B(x 2 ,y 2 ) 坐标，则向量 的坐标如何表示？ 2. 题 (2) 中由向量 对应的复数为 2+i ，则点 A 的坐标是多少 ? 【 探究提示 】 1. 因为向量 对应复数分别为 2 － 3i, － 3 +2i ，所以复平面内点的坐标是 (2,-3),(-3,2), =(2- (-3),-3-2). 2. 点 A 的坐标为 (2 ， 1). 【 自主解答 】 (1) 选 D. 向量 对应的复数分别为 2 － 3i, － 3+2i ，所以复平面内点的坐标是 A(2,-3),B(-3,2), 所以 =(5, － 5) ，所以 对应的复数是 5 － 5i. (2)① 设向量 对应的复数为 z 1 =x 1 +y 1 i(x 1 ， y 1 ∈R), 则点 B 的 坐标为 (x 1 ， y 1 ) ，由题意可知，点 A 的坐标为 (2 ， 1). 根据对称性可知： x 1 =2 ， y 1 =-1 ，故 z 1 =2-i. ② 设点 C 对应的复数为 z 2 =x 2 +y 2 i(x 2 ， y 2 ∈R), 则点 C 的坐标为 (x 2 ， y 2 ) ，由对称性可知： x 2 =-2 ， y 2 =-1 ， 故 z 2 =-2-i. 【 方法技巧 】 数形结合 , 探思路 (1) 以原点为起点的向量表示的复数等于它的终点对应的复数；向量平移后，此向量表示的复数不变，但平移前后起点、终点对应的复数要改变． (2) 复数的模从几何意义上来讲，表示复数对应的点到原点的距离，类比向量的模，可以进一步引申 |z － z 1 | 表示点 Z 到点 Z 1 之间的距离 . 如 |z － i|=1 表示点 Z 到点 (0 ， 1) 之间的距离为 1. 【 变式训练 】 复数 z ＝ 3 ＋ 4i 对应的向量 所在直线的 斜率为 _______ ． 【 解题指南 】 先利用复数与向量的对应关系，确定出向量 的坐标，再利用直线的斜率公式求直线斜率 . 【 解析 】 由 z ＝ 3 ＋ 4i 知， ＝ (3,4) ， 所以直线的斜率为 答案： 【 补偿训练 】 在复平面内画出下列复数对应的向量，并求出 各复数的模 . 【 解析 】 在复平面内分别画出点 Z 1 (1 ，－ 1) ， Z 3 ( － 2,0) ， Z 4 (2,2) ，则向量 分别为复数 z 1 ， z 2 ， z 3 ， z 4 对应的向量，如图所示． 各复数的模为 |z 1 | ＝ 【 规范解答 】 求两复数对应向量的夹角 【 典例 】 (12 分 ) 由已知两个向量 a , b 对应的复数分别是 z 1 ＝ 3 和 z 2 ＝－ 5 ＋ 5i ，求向量 a 与 b 的夹角． 【 审题 】 抓信息，找思路 【 解题 】 明步骤 , 得高分 【 点题 】 警误区 , 促提升 失分点 1: 解题时不能转化成①的形式 : 即不能利用复数、复平面上的点、向量间的一一对应关系进行相互转化导致不得分 . 失分点 2: 解题时由于知识遗忘不能得②式 : 由于不能熟记向量的夹角公式 , 导致最多得 6 分 . 失分点 3: 解题时由于 忽视向量夹角的范围③ , 在解题过程中 若忽视隐含条件 , 则会导致结论不确切而失去 1 分 . 【 悟题 】 提措施，导方向 复数与复平面上的点，与向量的对应 这种对应关系使得复数问题可以用几何方法解决，而几何问题也可以用复数方法解决 ( 即数形结合法 ) ，增加了解决复数问题的途径． 【 类题试解 】 已知两向量 a ， b 对应的复数分别是 z 1 ＝－ 3 ， z 2 ＋ mi(m∈R) ，且 a ， b 的夹角为 60° ，求 m 的值． 【 解析 】 因为 a ， b 对应的复数分别为 z 1 ＝－ 3 ， z 2 ＋ mi(m∈R) ，所以 a ＝ ( － 3,0) ， b ＝（ m ）． 又 a ， b 的夹角为 60° ，所以 cos 60° ＝