【数学】2020届一轮复习（理）通用版11-1算法初步学案 17页

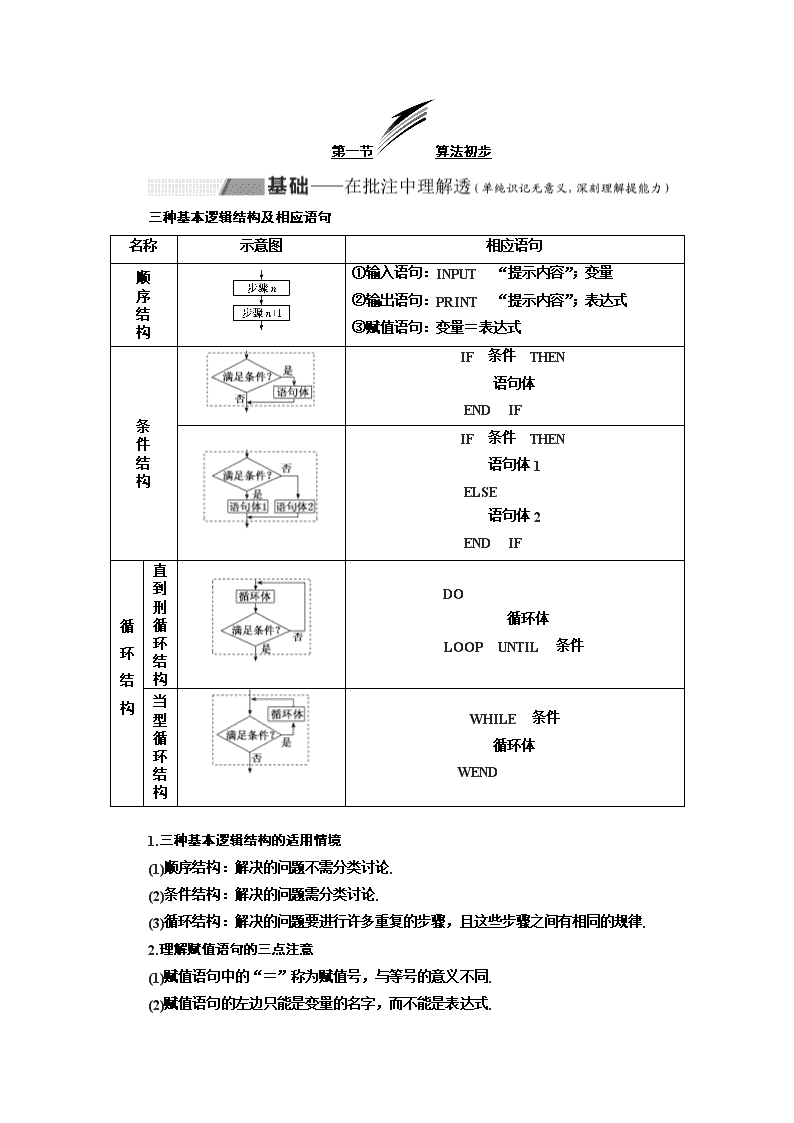
第一节算法初步 三种基本逻辑结构及相应语句 名称 示意图 相应语句 顺 序 结 构 ‎①输入语句：INPUT　“提示内容”；变量 ‎②输出语句：PRINT　“提示内容”；表达式 ‎③赋值语句：变量＝表达式 条 件 结 构 IF　条件　THEN　　‎ 语句体　　‎ END　IF IF　条件　THEN　　‎ 语句体1‎ ELSE 语句体2‎ END　IF 循 环 结构 直到刑循环结构 DO　　‎ ‎　　循环体 LOOP　UNTIL　条件 当型循环结构 ‎ ‎ WHILE　条件 循环体 WEND ‎1.三种基本逻辑结构的适用情境 ‎(1)顺序结构：解决的问题不需分类讨论.‎ ‎(2)条件结构：解决的问题需分类讨论.‎ ‎(3)循环结构：解决的问题要进行许多重复的步骤，且这些步骤之间有相同的规律.‎ ‎2.理解赋值语句的三点注意 ‎(1)赋值语句中的“＝”称为赋值号，与等号的意义不同.‎ ‎(2)赋值语句的左边只能是变量的名字，而不能是表达式.‎ ‎(3)对于同一个变量可以多次赋值，变量的值始终等于最近一次赋给它的值，先前的值将会被替换.‎ ‎3.注意选择结构与循环结构的联系 循环结构有重复性，选择结构具有选择性没有重复性，并且循环结构中必定包含一个选择结构，用于确定何时终止循环体.‎ ‎[小题查验基础]‎ 一、判断题(对的打“√”，错的打“×”)‎ ‎(1)算法的每一步都有确定的意义，且可以无限地运算.(　　)‎ ‎(2)一个程序框图一定包含顺序结构，也包含条件结构和循环结构.(　　)‎ ‎(3)一个循环结构一定包含条件结构.(　　)‎ ‎(4)当型循环是给定条件不成立时，执行循环体，反复进行，直到条件成立为止.(　　)‎ 答案：(1)×　(2)×　(3)√　(4)×‎ 二、选填题 ‎1.执行如图所示的程序框图，若输入x＝2，则输出的y值为(　　)‎ A.0　　　　　　　　　 B.1‎ C.2 D.3‎ 解析：选B　∵2＞0，∴y＝2×2－3＝1.‎ ‎2.执行如图所示的程序框图，则输出S的值为(　　)‎ A.10 B.17‎ C.19 D.36‎ 解析：选C　由程序框图可知：k＝2，S＝0；S＝2，k＝3；S＝5，k＝5；S＝10，k＝9；S＝19，k＝17，此时k＜10不成立，故退出循环，输出S＝19.‎ ‎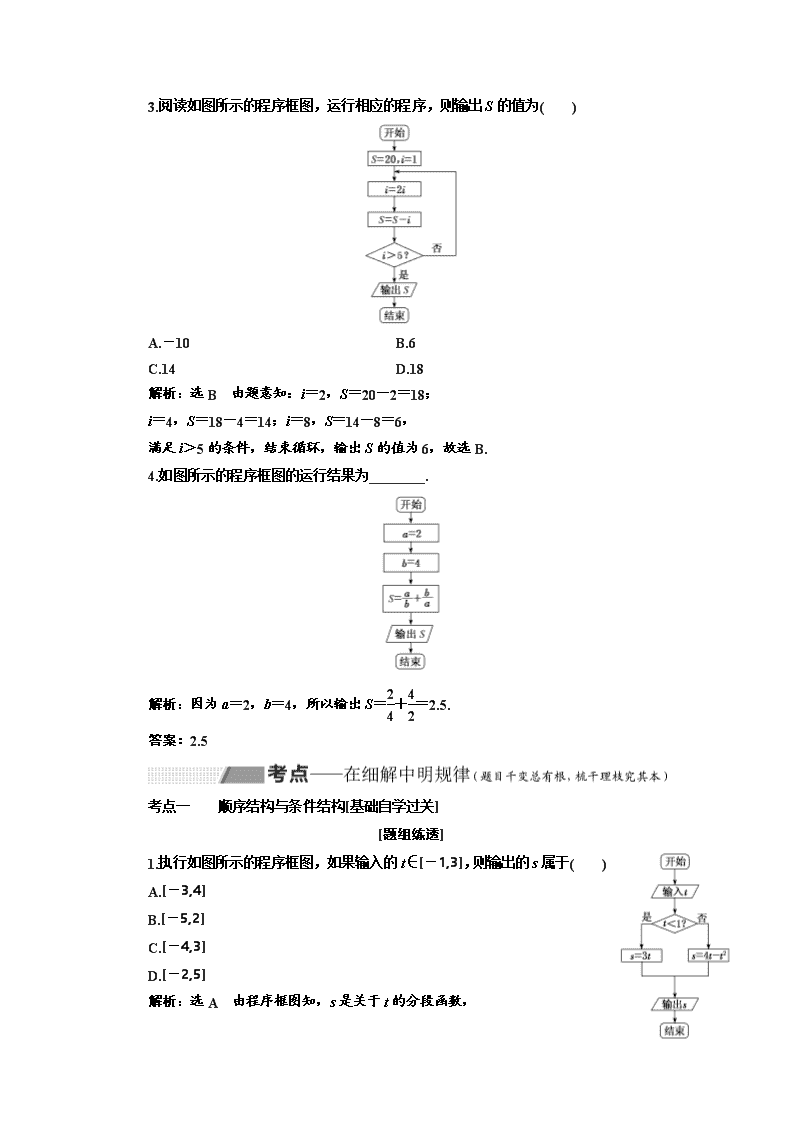3.阅读如图所示的程序框图，运行相应的程序，则输出S的值为(　　)‎ A.－10　　　　　　　　 B.6‎ C.14 D.18‎ 解析：选B　由题意知：i＝2，S＝20－2＝18；‎ i＝4，S＝18－4＝14；i＝8，S＝14－8＝6，‎ 满足i＞5的条件，结束循环，输出S的值为6，故选B.‎ ‎4.如图所示的程序框图的运行结果为________.‎ 解析：因为a＝2，b＝4，所以输出S＝＋＝2.5.‎ 答案：2.5‎ 考点一 顺序结构与条件结构[基础自学过关]‎ ‎[题组练透]‎ ‎1.执行如图所示的程序框图，如果输入的t∈[－1,3]，则输出的s属于(　　)‎ A.[－3,4]‎ B.[－5,2]‎ C.[－4,3]‎ D.[－2,5]‎ 解析：选A　由程序框图知，s是关于t的分段函数，‎ s＝ 当t∈[－1,1)时，s∈[－3,3)；‎ 当t∈[1,3]时，s＝4t－t2＝4－(t－2)2∈[3,4]，‎ 故s∈[－3,4]，故选A.‎ ‎2.执行如图所示的程序框图，当输入的x的值为4时，输出的y的值为2，则空白判断框中的条件可能为(　　)‎ A.x＞3?‎ B.x＞4?‎ C.x≤4?‎ D.x≤5?‎ 解析：选B　∵log24＝2,4＋2＝6，‎ ‎∴当x＝4时，应执行否.结合选项知选B.‎ ‎3.一算法的程序框图如图所示，若输出的y＝，则输入的x的值可能为(　　)‎ A.－1‎ B.0‎ C.1‎ D.5‎ 解析：选C　由程序框图知y＝ 当x＞2时，令y＝2x＝，解得x＝－1(舍去)；当x≤2时，令y＝sin＝，解得x＝12k＋1(k∈Z)或x＝12k＋5(k∈Z)，当k＝0时，x＝1或x＝5(舍去)，所以输入的x的值可能是1.‎ ‎4.定义[x]为不超过x的最大整数，例如[1.3]＝1.执行如图所示的程序框图，当输入的x为4.7时，输出的y值为(　　)‎ A.7　　　　　　　　 B.8.6‎ C.10.2 D.11.8‎ 解析：选C　当输入的x为4.7时，执行程序框图可知，4.7－[4.7]＝0.7，即4.7－[4.7]不等于0，因而可得y＝7＋([4.7－3]＋1)×1.6＝10.2，输出的y值为10.2.‎ ‎[名师微点]‎ 顺序结构和条件结构的运算方法 ‎(1)顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的.解决此类问题，只需分清运算步骤，赋值量及其范围进行逐步运算即可.‎ ‎(2)条件结构中条件的判断关键是明确条件结构的功能，然后根据“是”的分支成立的条件进行判断.‎ ‎(3)对于条件结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支.‎ 考点二 循环结构[全析考法过关]‎ ‎[考法全析]‎ 考法(一)　由程序框图求输出结果 ‎[例1]　(2018·洛阳第一次联考)执行如图所示的程序框图，若输入m＝209，n＝121，则输出的m的值为(　　)‎ A.0　　　　　　　　　 B.11‎ C.22 D.88‎ ‎[解析]　当m＝209，n＝121时，m除以n的余数r＝88，此时m＝121，n＝88，m除以n的余数r＝33，此时m＝88，n＝33，m除以n的余数r＝22，此时m＝33，n＝22，m除以n的余数r＝11，此时m＝22，n＝11，m除以n的余数r＝0，此时m＝11，n＝0，退出循环，输出m的值为11，故选B.‎ ‎[答案]　B 考法(二)　由输出结果判断输入变量的值 ‎[例2]　(1)(2019·安徽知名示范高中联考)执行如图所示的程序框图，如果输出的n＝2，那么输入的 a的值可以为(　　)‎ A.4 B.5‎ C.6 D.7‎ ‎(2)(2019·辽宁五校联考)我国古代数学著作《周髀算经》有如下问题：“今有器中米，不知其数.前人取半，中人三分取一，后人四分取一，余米一斗五升.问，米几何？”如图是解决该问题的程序框图，执行该程序框图，若输出的S＝1.5(单位：升)，则输入k的值为(　　)‎ A.4.5 B.6‎ C.7.5 D.9‎ ‎[解析]　(1)执行程序框图，输入a，P＝0，Q＝1，n＝0，此时P≤Q成立，P＝1，Q＝3，n＝1，此时P≤Q成立，P＝1＋a，Q＝7，n＝2.因为输出的n的值为2，所以应该退出循环，即P＞Q，所以1＋a＞7，结合选项，可知a的值可以为7，故选D.‎ ‎(2)由程序框图知S＝k－－－＝1.5，解得k＝6，故选B.‎ ‎[答案]　(1)D　(2)B 考法(三)　完善程序框图 ‎[例3]　(1)(2019·武汉调研)执行如图所示的程序框图，如果输入的a依次为2,2,5时，输出的s为17，那么在判断框中可以填入(　　)‎ A.k＜n? B.k＞n?‎ C.k≥n? D.k≤n?‎ ‎(2)(2018·全国卷Ⅱ)为计算S＝1－＋－＋…＋－，设计了如图所示的程序框图，则在空白框中应填入(　　)‎ A.i＝i＋1　　　　　　　 B.i＝i＋2‎ C.i＝i＋3 D.i＝i＋4‎ ‎[解析]　(1)执行程序框图，输入的a＝2，s＝0×2＋2＝2，k＝1；输入的a＝2，s＝2×2＋2＝6，k＝2；输入的a＝5，s＝2×6＋5＝17，k＝3，此时结束循环，又n＝2，所以判断框中可以填“k＞n？”，故选B.‎ ‎(2)由题意可将S变形为S＝－，则由S＝N－T，得N＝1＋＋…＋，T＝＋＋…＋.据此，结合N＝N＋，T＝T＋易知在空白框中应填入i＝i＋2.故选B.‎ ‎[答案]　(1)B　(2)B ‎[规律探求]‎ 看 个 性 考法(一)是由程序框图求输出结果，考法(二)是考法(一)的逆向求解问题.‎ 解决此类问题最常用的方法是列举法，即依次执行循环体中的每一步，直到循环终止，但在执行循环体的过程中：‎ ‎(1)要明确是当型循环结构还是直到型循环结构，根据各自特点执行循环体；‎ ‎(2)要明确框图中的累加变量，明确每一次执行循环体前和执行循环体后，变量的值发生的变化；‎ ‎(3)要明确循环终止的条件是什么，什么时候要终止执行循环体.‎ 考法(三)是完善程序框图问题.‎ 具体解题方法有以下两种：一是先假定空白处填写的条件，再正面执行程序，来检验填写的条件是否正确；二是根据结果进行回溯，直至确定填写的条件是什么 找 共 性 ‎1.求程序框图运行结果的思路 ‎(1)要明确程序框图中的顺序结构、条件结构和循环结构.‎ ‎(2)要识别运行程序框图，理解框图所解决的实际问题.‎ ‎(3)按照题目的要求完成解答并验证.‎ ‎2.确定控制循环变量的思路 结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式 ‎[过关训练]‎ ‎1.(2019·湘东五校联考)若[x]表示不超过x的最大整数，则如图所示的程序框图运行之后输出的结果为(　　)‎ A.600 B.400‎ C.15 D.10‎ 解析：选B　根据题意，得＝[4.975]＝4，所以该程序框图运行后输出的结果是40个0,40个1,40个2,40个3,40个4的和，所以输出的结果为S＝40＋40×2＋40×3＋40×4＝400.‎ ‎2.(2018·洛阳第一次统考)已知某算法的程序框图如图所示，则该算法的功能是(　　)‎ A.求首项为1，公差为2的等差数列的前2 018项和 B.求首项为1，公差为2的等差数列的前2 019项和 C.求首项为1，公差为4的等差数列的前1 010项和 D.求首项为1，公差为4的等差数列的前1 011项和 解析：选C　由程序框图得，输出的S＝(2×1－1)＋(2×3－1)＋(2×5－1)＋…＋(2×2 019－1)，可看作数列{2n－1}的前2 019项中所有奇数项的和，即首项为1，公差为4的等差数列的前1 010项和.故选C.‎ ‎3.(2019·河北“五个一名校联盟”模拟)执行如图所示的程序框图，输出的S值为－4时，条件框内应填写(　　)‎ A.i＞3？　　　　　　　　 B.i＜5?‎ C.i＞4? D.i＜4?‎ 解析：选D　由程序框图可知，S＝10，i＝1；S＝8，i＝2；S＝4，i＝3；S＝－4，i＝4.由于输出的S＝－4，故应跳出循环，选D.‎ ‎ ‎1.(2019·沈阳模拟)如图所示的程序框图，其作用是输入x的值，输出相应的y值，若x＝y，则这样的x的值有(　　)‎ A.1个　　　　　　　　 B.2个 C.3个 D.4个 解析：选C　当x≤2时，令y＝x2＝x⇒x(x－1)＝0，解得x＝0，或x＝1；当2＜x≤5时，令y＝2x－4＝x⇒x＝4；当x＞5时，令y＝＝x，无解.故这样的x的值有3个，故选C.‎ ‎2.(2019·合肥调研)执行如图所示的程序框图，则输出的S的值为(　　)‎ A.9 B.19‎ C.33 D.51‎ 解析：选C　m＝1，S＝1，满足条件；S＝1＋2×1＝3，m＝1＋2＝3，满足条件，S＝3＋2×3＝9，m＝3＋2＝5，满足条件；S＝9＋2×5＝19，m＝5＋2＝7，满足条件；S＝19＋2×7＝33，m＝7＋2＝9，不满足条件，输出的S的值为33.‎ ‎3.(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n－2n＞1 000的最小偶数n，那么在◇和▭两个空白框中，可以分别填入(　　)‎ A.A＞1 000和n＝n＋1 B.A＞1 000和n＝n＋2‎ C.A≤1 000和n＝n＋1 D.A≤1 000和n＝n＋2‎ 解析：选D　程序框图中A＝3n－2n，且判断框内的条件不满足时输出n，所以判断框中应填入A≤1 000，由于初始值n＝0，要求满足A＝3n－2n＞1 000的最小偶数，故执行框中应填入n＝n＋2.‎ ‎4.(2019·福州四校联考)执行如图所示的程序框图，则输出A的值是(　　)‎ A. B. C. D. 解析：选C　执行程序框图，可得，A＝1，i＝1，‎ 第1次执行循环体，A＝，i＝2，满足条件i≤20，‎ 第2次执行循环体，A＝，i＝3，满足条件i≤20，‎ 第3次执行循环体，A＝，i＝4，满足条件i≤20，‎ 第4次执行循环体，A＝，i＝5，满足条件i≤20，‎ 第5次执行循环体，A＝，i＝6，‎ ‎……‎ 观察可知，当i＝20时，满足条件i≤20，第20次执行循环体，A＝＝，i＝21，此时，不满足条件i≤20，退出循环，输出A的值为.故选C.‎ ‎5.(2019·南昌调研)执行如图所示的程序框图，则输出的n为(　　)‎ A.1 B.2‎ C.3 D.4‎ 解析：选C　当n＝1时，f(x)＝x′＝1，此时f(x)＝f(－x)，但f(x)＝0无解；当n＝2时，f(x)＝(x2)′＝2x，此时f(x)≠f(－x)；当n＝3时，f(x)＝(x3)′＝3x2，此时f(x)＝f(－x)，且f(x)＝0有解，此时结束循环，输出的n为3.‎ ‎6.(2018·南宁模拟)执行如图所示的程序框图，那么输出S的值是(　　)‎ A.－1 B. C.2 D.1‎ 解析：选C　S＝2，k＝2 016，判断2 016＜2 019；S＝＝－1，k＝2 016＋1＝2 017，判断2 017＜2 019；S＝＝，k＝2 017＋1＝2 018，判断2 018＜2 019；S＝＝2，k＝2 018＋1＝2 019，判断2 019＜2 019不成立，输出S，此时S＝2.‎ ‎7.(2019·合肥质检)执行如图所示的程序框图，若输入的n等于10，则输出的结果是(　　)‎ A.2 B.－3‎ C.－ D. 解析：选C　n＝10，a＝2，i＝1＜10；a＝＝－3，i＝2＜10；‎ a＝＝－，i＝3＜10；a＝＝，i＝4＜10；‎ a＝＝2，i＝5＜10；a＝＝－3，i＝6＜10；‎ a＝－，i＝7＜10；a＝，i＝8＜10；a＝2，i＝9＜10；‎ a＝－3，i＝10；a＝－，i＝11＞10，退出循环.‎ 则输出的a＝－.‎ ‎8.(2019·昆明调研)定义[x]表示不超过x的最大整数，例如[2]＝2，[3.6]＝3，如图所示的程序框图取材于中国古代数学著作《孙子算经》.执行该程序框图，则输出的a＝(　　)‎ A.9 B.16‎ C.23 D.30‎ 解析：选C　由程序框图得k＝1，a＝9，a－3·＝0≠2，k＝2，a＝16，a－3·＝1≠2，k＝3，a＝23，a－3·＝2，a－5·＝3，退出循环体，所以输出a＝23，故选C.‎ ‎9.(2019·西安质检)执行如图所示的程序框图，设输出的数据构成的集合为A，从集合A中任取一个元素a，则函数y＝xa，x∈[0，＋∞)是增函数的概率为(　　)‎ A. B. C. D. 解析：选C　由程序框图得x＝－3，y＝3；x＝－2，y＝0；x＝－1，y＝－1；x＝0，y＝0；x＝1，y＝3；x＝2，y＝8；x＝3，y＝15；x＝4，退出循环.则集合A中的元素有－1,0,3,8,15，共5个，若函数y＝xa，x∈[0，＋∞)为增函数，则a＞0，所以所求的概率为.‎ ‎10.美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算，他们创造了优良的计数系统，其中开平方算法是最具有代表性的.程序框图如图所示，若输入a，n，f的值分别为8,2,0.5，每次运算都精确到小数点后两位，则输出的结果为(　　)‎ A.2.81 B.2.82‎ C.2.83 D.2.84‎ 解析：选D　输入a＝8，n＝2，f＝0.5，‎ 则m＝＝4，n＝＝3，|4－3|＝1＞0.5；‎ m＝≈2.67，n≈＝2.84，|2.67－2.84|＝0.17＜0.5，输出n＝2.84.故选D.‎ ‎11.(2019·成都诊断)高三某班15名学生一次模拟考试成绩用茎叶图表示如图1.执行图2所示的程序框图，若输入的ai(i＝1,2，…，15)分别为这15名学生的考试成绩，则输出的结果为(　　)‎ A.6 B.7‎ C.8 D.9‎ 解析：选D　由程序框图可知，其统计的是成绩大于或等于110的人数，所以由茎叶图知，成绩大于或等于110的人数为9，因此输出的结果为9.故选D.‎ ‎12.(2018·郑州第一次质量预测)执行如图所示的程序框图，若输出的结果是7，则判断框内m的取值范围是(　　)‎ A.(30,42] B.(30,42)‎ C.(42,56] D.(42,56)‎ 解析：选A　初始值：k＝1，S＝0，进入循环，S＝2，k＝2，S＝2＋4＝6，k＝3，S＝6＋6＝12，k＝4，S＝12＋8＝20，k＝5，S＝20＋10＝30，k＝6，S＝30＋12＝42，k＝7，此时不满足S＝42＜m，退出循环，所以30＜m≤42，故选A.‎ ‎13.(2019·石家庄模拟)如图是计算1＋＋＋…＋的值的程序框图，则图中①②处可以填写的语句分别是(　　)‎ A.n＝n＋2，i＞16? B.n＝n＋2，i≥16?‎ C.n＝n＋1，i＞16? D.n＝n＋1，i≥16?‎ 解析：选A　式子1＋＋＋…＋中所有项的分母构成公差为2的等差数列，1,3,5，…，31,31＝1＋(k－1)×2，k＝16，共16项，故选A.‎ ‎14.执行如图所示的程序框图，输出的s的值为________.‎ 解析：由框图知，输出的s为数列的前2 019项和.因为数列中项的值以6为周期重复出现，且前6项和等于0，又2 019＝6×336＋3，所以数列的前2 019项和等于336×0＋sin＋sin＋sin π＝，即输出的s的值为.‎ 答案： ‎15.263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的n的值为________.‎ ‎(参考数据：sin 15°≈0.258 8，sin 7.5°≈0.130 5)‎ 解析：n＝6，S＝≈2.598＜3.10，n＝12；S＝3＜3.10，n＝24；S≈3.105 6≥3.10，满足条件，退出循环.故输出的n的值为24.‎ 答案：24‎