【数学】2018届一轮复习人教A版（理）1-1集合及其运算学案 16页

‎§1.1　集合及其运算 考纲展示►　‎ ‎1.了解集合的含义，体会元素与集合的属于关系．‎ ‎2．理解集合之间包含与相等的含义，能识别给定集合的子集．‎ ‎3．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集．‎ ‎4．理解在给定集合中一个子集的补集的含义，会求给定子集的补集．‎ ‎5．能使用韦恩(Venn)图表达集合间的基本关系及运算．‎ 考点1　集合的基本概念 元素与集合 ‎(1)集合元素的特性：________、________、无序性．‎ ‎(2)集合与元素的关系：若a属于集合A，记作________；若b不属于集合A，记作________．‎ ‎(3)集合的表示方法：________、________、图示法．‎ ‎(4)常见数集及其符号表示：‎ 数集 自然数集 正整数集 整数集 有理数集 实数集 符号 ‎________‎ N*或N＋‎ Z Q R 答案：(1)确定性　互异性　(2)a∈A　b∉A　(3)列举法　描述法　(4)N 集合表示的两个误区：集合的代表元素；图示法．‎ ‎(1)已知集合A＝{y|y＝sin x}，B＝{x|y＝sin x}，则A∩B＝________.‎ 答案：[－1,1]‎ 解析：集合A表示的是函数y＝sin x的值域，即A＝[－1,1]；集合B表示的是函数y＝sin x的定义域，即B＝R，所以A∩B＝[－1,1]．‎ ‎(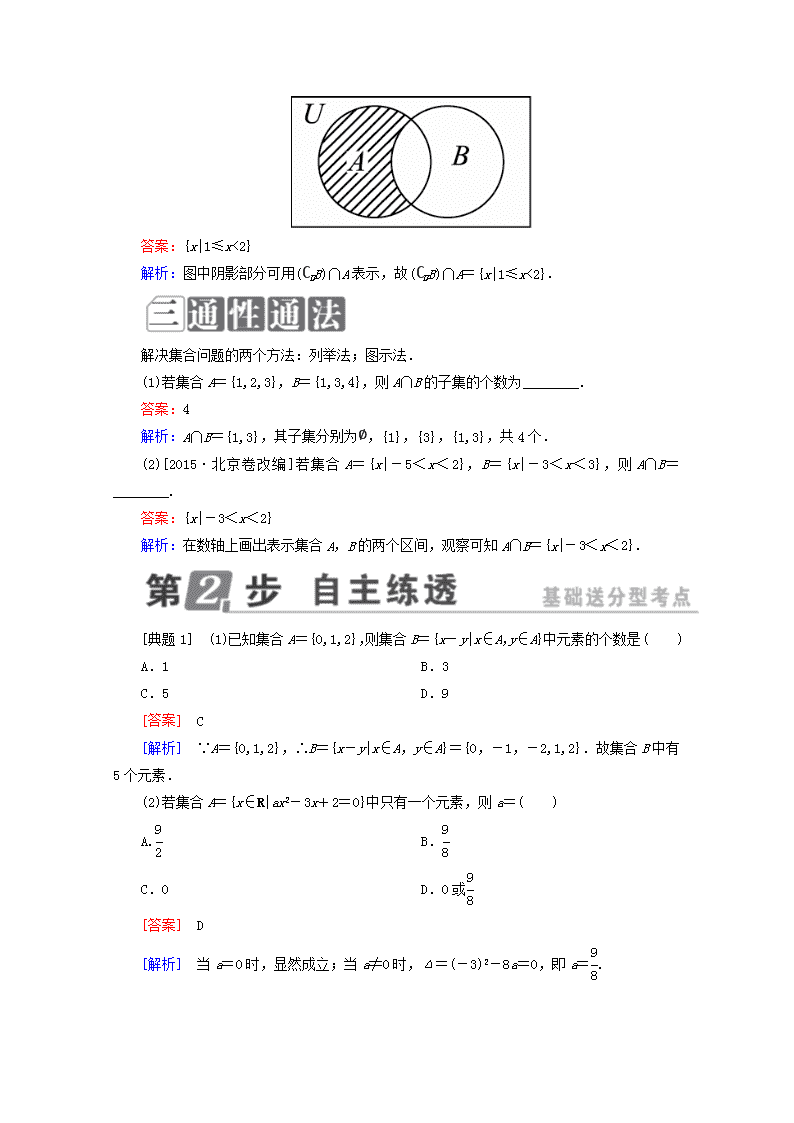2)设全集U＝R，A＝{x|0＜x＜2}，B＝{x|x＜1}，则图中阴影部分表示的集合为________．‎ 答案：{x|1≤x<2}‎ 解析：图中阴影部分可用(∁UB)∩A表示，故(∁UB)∩A＝{x|1≤x<2}．‎ 解决集合问题的两个方法：列举法；图示法．‎ ‎(1)若集合A＝{1,2,3}，B＝{1,3,4}，则A∩B的子集的个数为________．‎ 答案：4‎ 解析：A∩B＝{1,3}，其子集分别为∅，{1}，{3}，{1,3}，共4个．‎ ‎(2)[2015·北京卷改编]若集合A＝{x|－5＜x＜2}，B＝{x|－3＜x＜3}，则A∩B＝________.‎ 答案：{x|－3＜x＜2}‎ 解析：在数轴上画出表示集合A，B的两个区间，观察可知A∩B＝{x|－3＜x＜2}．‎ ‎[典题1]　(1)已知集合A＝{0,1,2}，则集合B＝{x－y|x∈A，y∈A}中元素的个数是(　　)‎ A．1 B．3‎ C．5 D．9‎ ‎[答案]　C ‎[解析]　∵A＝{0,1,2}，∴B＝{x－y|x∈A，y∈A}＝{0，－1，－2,1,2}．故集合B中有5个元素．‎ ‎(2)若集合A＝{x∈R|ax2－3x＋2＝0}中只有一个元素，则a＝(　　)‎ A. B． C．0 D．0或 ‎[答案]　D ‎[解析]　当a＝0时，显然成立；当a≠0时，Δ＝(－3)2－‎8a＝0，即a＝. ‎ ‎(3)设a，b∈R，集合{1，a＋b，a}＝，则b－a＝(　　)‎ A．1 B．－1‎ C．2 D．－2‎ ‎[答案]　C ‎[解析]　因为{1，a＋b，a}＝，a≠0，‎ 所以a＋b＝0，则＝－1，‎ 所以a＝－1，b＝1，所以b－a＝2.‎ ‎(4)已知集合A＝{m＋2,‎2m2‎＋m}，若3∈A，则m的值为________．‎ ‎[答案]　－ ‎[解析]　由题意得m＋2＝3或‎2m2‎＋m＝3，则m＝1或m＝－.当m＝1时，m＋2＝3且‎2m2‎＋m＝3，根据集合中元素的互异性可知不满足题意；当m＝－时，m＋2＝，而‎2m2‎＋m＝3，故m＝－.‎ ‎[点石成金]　与集合中的元素有关问题的求解策略 ‎(1)用描述法表示集合，首先要搞清楚集合中代表元素的含义，再看元素的限制条件，明白集合的类型，是数集、点集还是其他类型集合．‎ ‎(2)集合中元素的三个特性中的互异性对解题的影响较大，特别是含有字母的集合，在求出字母的值后，要注意检验集合中的元素是否满足互异性．‎ 考点2　集合间的基本关系 集合间的基本关系 表示 关系　　　　‎ 文字语言 记法 集合 间的 基本 子集 集合A中任意一个元素都是集合B中的元素 ‎__________或__________‎ 关系 真子集 集合A是集合B的子集，并且B ‎__________或__________‎ 中至少有一个元素不属于A 相等 集合A的每一个元素都是集合B的元素，集合B的每一个元素也都是集合A的元素 A⊆B且B⊆A⇔A＝B 空集 空集是________集合的子集 ‎∅⊆A 空集是________集合的真子集 ‎∅B且B≠∅‎ 答案：A⊆B　B⊇A　AB　BA　任何　‎ 任何非空 集合中的两个易混结论：集合中元素的个数；集合的子集的个数．‎ ‎(1)[2015·江苏卷]已知集合A＝{1,2,3}，B＝{2,4,5}，则集合A∪B中元素的个数为________．‎ 答案：5‎ 解析：因为A∪B＝{1,2,3,4,5}，所以A∪B中元素的个数为5.‎ ‎(2)集合A＝{1,4,7,10,13,16,19,21}，则集合A有________个子集、________个真子集、________个非空子集、________个非空真子集．‎ 答案：28　28－1　28－1　28－2‎ 解析：因为集合A中有8个元素，所以集合A有28个子集，28－1个真子集，28－1个非空子集，28－2个非空真子集．‎ ‎[典题2]　(1)设P＝{y|y＝－x2＋1，x∈R}，Q＝{y|y＝2x，x∈R}，则(　　)‎ A．P⊆Q B．Q⊆P C．∁RP⊆Q D．Q⊆∁RP ‎[答案]　C ‎[解析]　因为P＝{y|y＝－x2＋1，x∈R}＝{y|y≤1}，Q＝{y|y＝2x，x∈R}＝{y|y>0}，所以∁RP＝{y|y>1}，所以∁RP⊆Q，故选C.‎ ‎(2)已知集合A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0＜x＜5，x∈N}，则满足条件A⊆C⊆B的集合C的个数为(　　)‎ A．1 B．2 ‎ C．3 D．4‎ ‎[答案]　D ‎[解析]　由x2－3x＋2＝0得x＝1或x＝2，‎ ‎∴A＝{1,2}．‎ 由题意知B＝{1,2,3,4}，‎ ‎∴满足条件的C可为{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}．‎ ‎(3)已知集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤‎2m－1}，若B⊆A，则实数m的取值范围为________．‎ ‎[答案]　(－∞，3]‎ ‎[解析]　∵B⊆A，‎ ‎∴①若B＝∅，则‎2m－1a}，若M⊆N，则实数a的取值范围是(　　)‎ A．(－∞，－1] B．(－∞，－1)‎ C．[3，＋∞) D．(3，＋∞)‎ 答案：A 解析：M＝{x|(x－3)(x＋1)<0}＝(－1,3)，又M⊆N，因此有a≤－1，即实数a的取值范围是(－∞，－1]．‎ 考点3　集合的基本运算 集合的基本运算 ‎(1)三种基本运算的概念及表示：‎ 集合的并集 集合的交集 集合的补集 符号表示 ‎________‎ ‎________‎ 若全集为U，则集合A的补集为________‎ 图形表示 意义 ‎{x|________}‎ ‎{x|________}‎ ‎∁U A＝________________‎ ‎(2)三种运算的常见性质：‎ ‎①A∪B＝A⇔B⊆A，A∩B＝A⇔A⊆B.‎ ‎②A∩A＝________，A∩∅＝________.‎ ‎③A∪A＝________，A∪∅＝________.‎ ‎④A∩(∁UA)＝________，A∪(∁UA)＝________，‎ ‎∁U(∁UA)＝________.‎ ‎⑤A⊆B⇔A∩B＝A⇔A∪B＝B⇔∁UA⊇∁UB⇔A∩(∁UB)＝∅.‎ 答案：(1)A∪B　A∩B　∁UA　x∈A，或x∈B x∈A，且x∈B　{x|x∈U，且x∉A}　‎ ‎(2)②A　∅　③A　A　④∅　U　A ‎(1)[教材习题改编]满足{0,1}⊆A{0,1,2,3}的集合A的个数为(　　)‎ A．1 B．2 ‎ C．3 D．4‎ 答案：C 解析：A中包含元素0,1，还有集合{2,3}真子集中的元素，{2,3}的真子集有22－1＝3(个)．‎ ‎(2)[教材习题改编]已知集合A＝{1,2}，B＝{x|ax－1＝0}，且A∪B＝A，则a的值可为________．‎ 答案：1或或0‎ 解析：A∪B＝A⇒BA，若B＝∅，则a＝0；若1∈B⇒a＝1；若2∈B⇒a＝.‎ 集合中两组常用结论：集合间的基本关系；集合的运算．‎ ‎(1)A⊆B⇔A∩B＝A⇔A∪B＝B⇔∁UA⊇∁UB⇔A∩(∁UB)＝∅.‎ ‎(2)(∁UA)∩(∁UB)＝________，(∁UA)∪(∁UB)＝________.‎ 答案：∁U(A∪B)　∁U(A∩B)‎ 解析： 设x∈∁U(A∪B)，则x∉A∪B，得x∉A且x∉B，即x∈∁UA且x∈∁UB，即x∈(∁UA)∩(∁UB)，即∁U(A∪B)⊆(∁UA)∩(∁UB)；反之，当x∈(∁UA)∩(∁UB)时，得x∈∁UA且x∈∁UB，得x∉A且x∉B，则x∉A∪B，所以x∈∁U(A∪B)，即∁U(A∪B)⊇(∁UA)∩(∁UB)．根据集合相等的定义，得∁U(A∪B)＝(∁UA)∩(∁UB)．同理可证另一结论．‎ ‎[考情聚焦]　有关集合运算的考题，在高考中多以选择题或填空题的形式呈现，试题难度不大，多为低档题，集合运算多与解简单的不等式、函数的定义域、值域相联系，考查对集合的理解及不等式的有关知识；有些集合题为抽象集合题或新定义型集合题，考查学生灵活处理问题的能力．‎ 主要有以下几个命题角度：‎ 角度一 离散型数集间的交、并、补运算 ‎[典题3]　[2017·湖南株洲模拟]设全集U＝{0,1,2,3,4,5}，集合A＝{2,4}，B＝{y|y＝log (x－1)，x∈A}，则集合(∁UA)∩(∁UB)＝(　　)‎ A．{0,4,5,2} B．{0,4,5}‎ C．{2,4,5} D．{1,3,5}‎ ‎[答案]　D ‎[解析]　由题意知B＝{0,2}，∴∁UA＝{0,1,3,5}，∁UB＝{1,3,4,5}，∴(∁UA)∩(∁UB)＝{1,3,5}．‎ 角度二 连续型数集间的交、并、补运算 ‎[典题4]　(1)设全集U＝R，A＝{x|x(x＋3)<0}，B＝{x|x<－1}，则图中阴影部分表示的集合为(　　)‎ A．{x|－30}，则A∩B＝(　　)‎ A. B． C. D． 答案：D 解析：由题意得，A＝{x|10}，则S∩T＝(　　)‎ A．[2,3] ‎ B．(－∞，2]∪[3，＋∞)‎ C．[3，＋∞) ‎ D．(0,2]∪[3，＋∞)‎ 答案：D 解析：集合S＝(－∞，2]∪[3，＋∞)，结合数轴，可得S∩T＝(0,2]∪[3，＋∞)．‎ ‎4．[2015·新课标全国卷Ⅱ]已知集合A＝{－2，－1，0,1,2}，B＝{x|(x－1)(x＋2)<0}，则A∩B＝(　　)‎ A．{－1,0} B．{0,1} ‎ C．{－1,0,1} D．{0,1,2}‎ 答案：A 解析：由题意知B＝{x|－20}，B＝{x|2