2019-2020学年河北省邢台市第八中学高一上学期期中数学试题（解析版） 13页

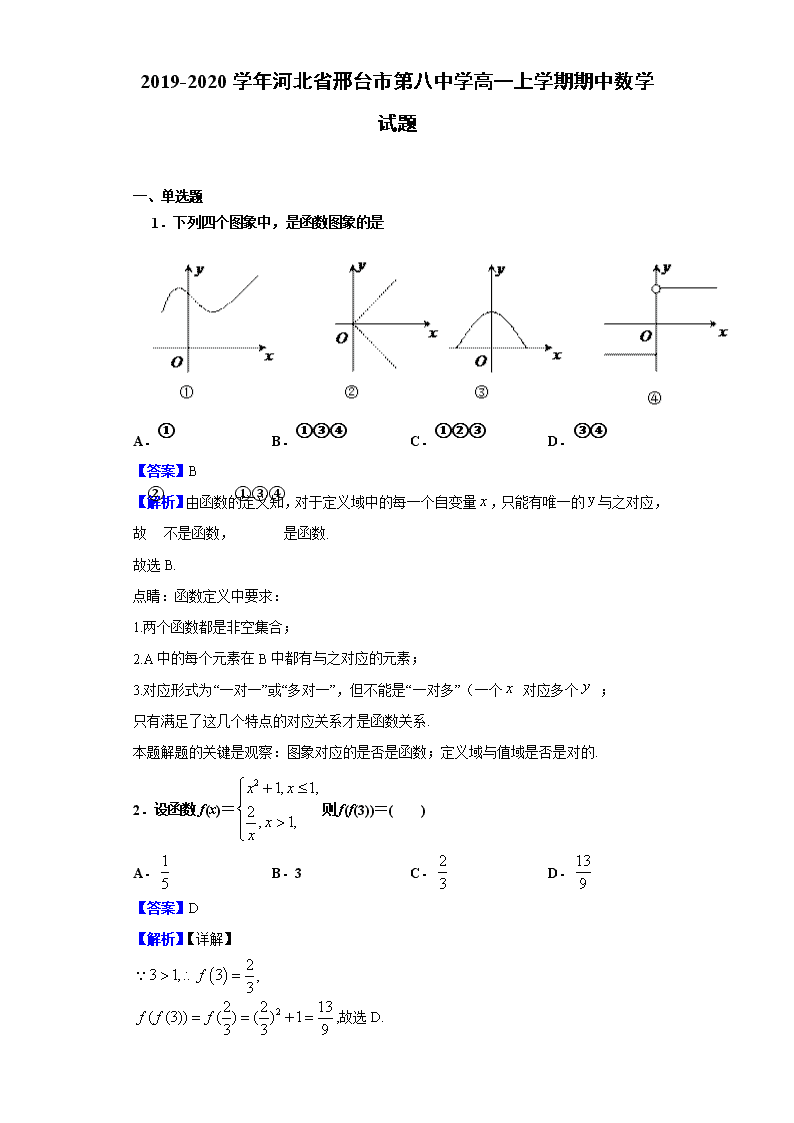
‎2019-2020学年河北省邢台市第八中学高一上学期期中数学试题 一、单选题 ‎1．下列四个图象中，是函数图象的是 A．① B．①③④ C．①②③ D．③④‎ ‎【答案】B ‎【解析】由函数的定义知，对于定义域中的每一个自变量，只能有唯一的与之对应，故②不是函数，①③④是函数.‎ 故选B.‎ 点睛：函数定义中要求：‎ ‎1.两个函数都是非空集合；‎ ‎2.A中的每个元素在B中都有与之对应的元素；‎ ‎3.对应形式为“一对一”或“多对一”，但不能是“一对多”（一个 对应多个 ；‎ 只有满足了这几个特点的对应关系才是函数关系.‎ 本题解题的关键是观察：图象对应的是否是函数；定义域与值域是否是对的.‎ ‎2．设函数f(x)＝则f(f(3))＝(　　)‎ A． B．3 C． D．‎ ‎【答案】D ‎【解析】【详解】‎ ‎,‎ ‎,故选D.‎ ‎3．下列各组函数表示同一个函数的是（ ）.‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】根据同一函数的定义,对四个选项中的每对函数都求出定义域,如果定义域相同,再通过对应关系上看是不是同一函数.‎ ‎【详解】‎ 选项A：函数的定义域是全体实数集,函数的定义域是全体非负实数集,故两个函数不是同一函数；‎ 选项B：函数的定义域是全体实数集,函数的定义域是全体非零实数集,故两个函数不是同一函数；‎ 选项C：函数的定义域是全体实数集,函数的定义域是全体实数集,且对应关系一样,故两个函数是同一函数；‎ 选项D：函数的定义域是全体实数集,函数的定义域是不等于1的实数集,故两个函数不是同一函数；‎ 故选：C.‎ ‎【点睛】‎ 本题考查了同一函数的判断,正确求出每个函数的定义域是解题的关键.‎ ‎4．已知是一次函数,且满足,则（ ）.‎ A． B． C． D．‎ ‎【答案】A ‎【解析】设出一次函数的解析式,利用,得到等式,列出方程组,解方程组即可求出的解析式.‎ ‎【详解】‎ 因为是一次函数,所以设,‎ 由,得.‎ 整理得,‎ 所以,解得.‎ 故选：A.‎ ‎【点睛】‎ 本题考查了用待定系数法求函数解析式,考查了数学运算能力.‎ ‎5．函数y＝的单调递减区间为( )‎ A．(－∞，－3] B．(－∞，－1]‎ C．[1，＋∞) D．[－3，－1]‎ ‎【答案】A ‎【解析】该函数的定义域为(－∞，－3]∪[1，＋∞)，函数f(x)＝x2＋2x－3的对称轴为x＝－1，由复合函数的单调性可知该函数在区间(－∞，－3]上是减函数．‎ ‎6．已知定义在R上的奇函数,当时, ,那么当时, 的解析式为（ ）.‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】根据奇函数的定义,可以直接写出当时, 的解析式.‎ ‎【详解】‎ 解：设,则,‎ ‎∵‎ ‎∴.‎ 故选：D ‎【点睛】‎ 本题考查了利用函数的奇偶性求函数解析式,考查了奇函数的性质.‎ ‎7．函数y=ax在[0，1]上最大值与最小值的和为3，则a=‎ A．2 B． C．4 D．‎ ‎【答案】A ‎【解析】y=ax在[0，1]上是单调函数，即当x=0和1时，y=ax取得最值，代入即可得到最值.‎ ‎【详解】‎ y=ax在[0，1]上是单调函数，即当x=0和1时，y=ax取得最值，由题意，a0+a1=3，即1+a=3，所以a=2，‎ 故选A．‎ ‎【点睛】‎ 这个题目考查了指数函数的单调性问题，指数函数的单调性由a和1的大小关系决定，当a>1时，函数单增，当0