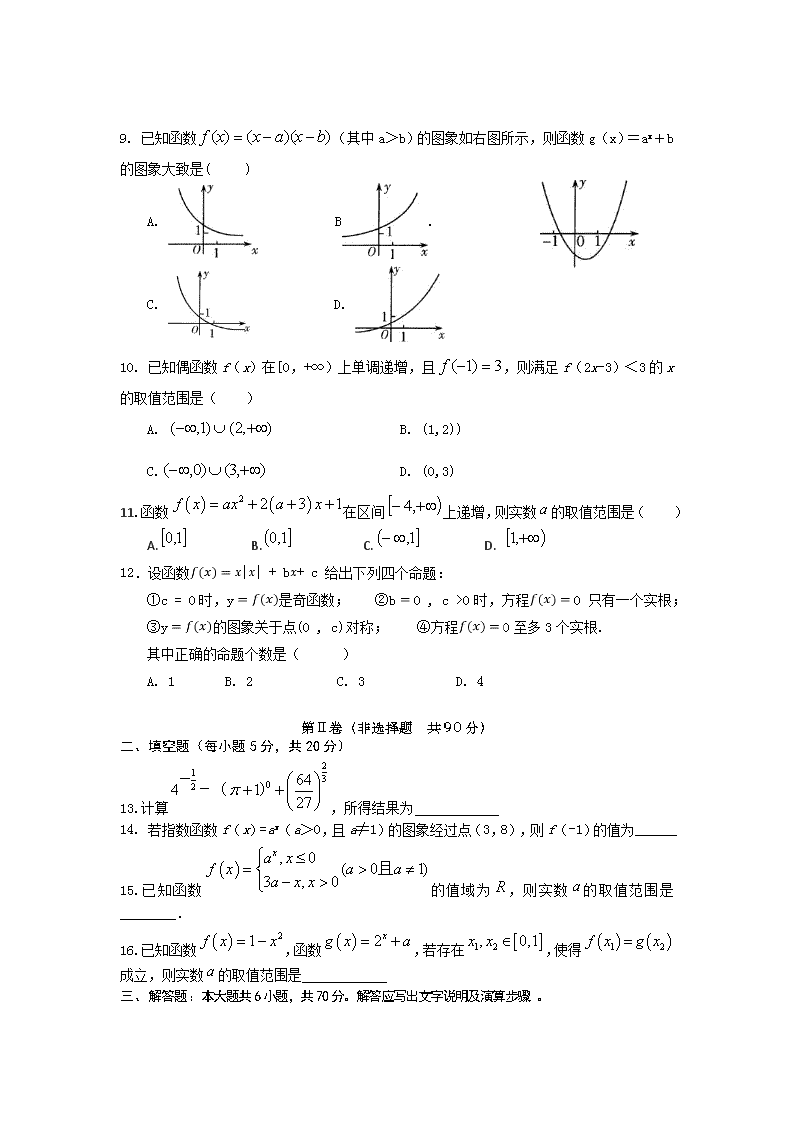2018-2019学年福建省漳平市第一中学高一上学期第一次月考数学试题 10页

‎2018-2019学年福建省漳平市第一中学高一上学期第一次月考数学试题 ‎（考试时间：120分钟 总分：150分）‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.下列各个关系式中，正确的是（　　）‎ A. ={0} B. C. {3，5}≠{5，3} D. {1}⊆{x|x2=x}‎ ‎2.已知集合，则（ ）‎ A. B. C. D. ‎ ‎3. 函数y=ax-3+1（a＞0且a≠1）图象一定过点（　　）‎ A. （0，1） B. （3，1） C. （0，2） D. （3，2）‎ ‎4. 已知f（2x+1）=x2+x，则f（3）=( )‎ A． B． C． D．‎ ‎5. 已知函数，则其图象( )‎ A.关于轴对称 B.关于直线对称 C.关于原点对称 D.关于轴对称 ‎6. 已知f（x）=，则f[f（3）]=（　　）‎ A. 3 B. -10 C. -3 D. 10‎ ‎7. 设全集为R,函数的定义域为M,则=　(　 　)‎ A. B. C. D.‎ ‎8. 设,则　(　 　)‎ A. B. C. D. ‎ ‎9. 已知函数（其中a＞b）的图象如右图所示，则函数g（x）＝ax＋b的图象大致是(       )‎ A. B. ‎ C. D. ‎ ‎10. 已知偶函数f（x）在[0，+∞）上单调递增，且，则满足f（2x-3）＜3的x的取值范围是（　　）‎ A. B. (1,2))‎ C. D. (0,3)‎ ‎11.函数在区间上递增，则实数的取值范围是（　 ）‎ A. B. C. D. ‎ ‎12．设函数|| + b+ c 给出下列四个命题：‎ ‎①c = 0时，y是奇函数；     ②b0 , c >0时，方程0 只有一个实根； ‎ ‎③y的图象关于点(0 , c)对称；        ④方程0至多3个实根.‎ 其中正确的命题个数是（   ）‎ A. 1 B. 2 C. 3 D. 4‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题（每小题5分，共20分）‎ ‎13.计算，所得结果为 ‎ ‎14. 若指数函数f（x）=ax（a＞0，且a≠1）的图象经过点（3，8），则f（-1）的值为______‎ ‎15.已知函数的值域为，则实数的取值范围是________．‎ ‎16.已知函数，函数，若存在，使得成立，则实数的取值范围是 ‎ 三、解答题：本大题共6小题，共70分。解答应写出文字说明及演算步骤.。‎ ‎17. （本题满分10分）已知集合．‎ ‎（1）当m=2时，求A∪B；.‎ ‎（2）若B⊆A，求实数m的取值范围．‎ ‎18. （本题满分12分）若集合，.‎ ‎（1）若,求实数的值； ‎ ‎（2）若，求实数的取值范围．‎ ‎19. （本题满分12分）设函数是奇函数.‎ ‎（1）求常数的值.‎ ‎（2）若,试判断函数的单调性,并用定义加以证明.‎ ‎20、（本题满分12分）已知函数f（x）是定义域为R的偶函数，当时，f（x）=x2-2x ‎（1）求出函数f（x）在R上的解析式；‎ ‎（2）画出函数f（x）的图象，并根据图象写出f（x）的单调区间．‎ ‎（3）求使f（x）=1时的x的值．‎ ‎21. （本题满分12分）已知二次函数的最小值等于4，且 ‎（1）求函数的解析式；‎ ‎（2）设函数，且函数在区间上是单调函数，求实数的取值范围；‎ ‎（3）设函数，求当时，函数的值域．‎ ‎22. （本题满分12分）已知函数f（x）的定义域为R，且对任意的x，y∈R有f（x+y）=f（x）+f（y）‎ 当 x＞0时，f（x）＞0，f（1）=1‎ ‎（1）求f（0），f（3）的值；‎ ‎（2）判断f（x）的单调性并证明；‎ ‎（3）若f（4x-a）+f（6+2x+1）＞2对任意x∈R恒成立，求实数a的取值范围．‎ 漳平一中2018-2019学年第一学期第一次月考高一数学试题答案 一、选择题 DBDCCD AADBAD 二、填空题 ‎13, 14, 15, 16,‎ 三、解答题 ‎17. 解：解：（1）当m=2时，A={x|-1≤x≤5},...........................1分 由B中不等式变形得3-2≤3x≤34，解得-2≤x≤4，即B={x|-2≤x≤4}．.......3分 ∴A∪B={x|-2≤x≤5}．. ..................5分 （2）∵B⊆A，∴，解得m≥3， .................9分 ∴m的取值范围为{m|m≥3} .................10分 ‎18. 解：（1） ．.................1分 ‎ ‎ .................2分 ‎ .................3分 ‎ .................4分 当时，满足；当，满足..........5分 ‎ .................6分 ‎（2）由已知得 .................7分 ‎① 若时，，得，此时………8分 ‎② 若为单元素集时，，，当时，；…9分 ‎③ 若为二元素集时，则，，此时无解。..11分 综上所述：实数的取值范围是………………12分 ‎19. 解 (1)函数的定义域为R,‎ 因为函数是奇函数.‎ 所以，所以. .................2分 经检验得，符合题意。（用定义求的不需要检验） ………………4分 ‎(2)函数在上为单调减函数, ……………………5分 证明如下: ，设，且，…………6分 ‎ ……………………………..10分 ‎，即 所以函数在上为单调减函数。…………………….12分 ‎20、解：（1）当x＜0时，-x＞0，因为f（x）是偶函数，所以f（-x）=f（x）．……（2分） 所以f（x）=f（-x）=x2+2x． ………………………（3分） 综上：f（x）= ……………………………（4分）． （2）图象如图所示． 单调增区间：[-1，0]，[1，+∞） 单调减区间：（-，-1）,(0,1) …………………………（8分）． （3）当x＞0时，x2-2x=1 解得 因为x＞0，所以 当x＜0时，x2+2x=1，解得x=-1-或，‎ 因为x＜0，所以x=-1- 综上所述，…………………………………（12分）‎ ‎21.解:（1），‎ 设，‎ ‎ …………………3分 ‎（2）函数，其对称轴方程是 ‎ ‎∵函数在区间上是单调函数， ∴ ，‎ ‎ ∴或，∴实数的取值范围是…………………6分 （3）令 则………………8分 当单调递减；当，单调递增；…………………9分 ‎，…………………………V10分 又，所以……………………11分 当时，函数的值域是………………….12分 ‎22.解：解：（Ⅰ）令x=y=0，得f（0+0）=f（0）+f（0），所以f（0）=0． 由f（1）=1，得f（2）=f（1）+f（1）=1+1=2， f（3）=f（2）+f（1）=2+1=3．…（2分） （Ⅱ）f（x）在R上是增函数，证明如下： 任取x1，x2∈R，且x1＜x2，则x2-x1＞0，且f（x2-x1）＞0， 所以f（x2）-f（x1）=f（x2-x1+x1）-f（x1） =f（x2-x1）+f（x1）-f（x1）=f（x2-x1）＞0， 即f（x1）＜f（x2），所以f（x）在R上是增函数．…（6分） （Ⅲ）由f（4x-a）+f（6+2x+1）＞2对任意 x∈R恒成立， 得f（4x-a+6+2x+1）＞f（2）恒成立． 因为f（x）在R上是增函数，所以4x-a+6+2x+1＞2恒成立， 即4x+2•2x+4＞a恒成立…（8分） 令g（x）=4x+2•2x+4=（2x+1）2+3， 因为2x＞0，所以g（x）＞4…（10分） 故a≤4…（12分）‎ 漳平一中2018-2019学年第一学期第一次月考高一数学试题答案 一、选择题 DBDCCD AADBAD 二、填空题 ‎13, 14, 15, 16,‎ 三、解答题 ‎17. 解：解：（1）当m=2时，A={x|-1≤x≤5},...........................1分 由B中不等式变形得3-2≤3x≤34，解得-2≤x≤4，即B={x|-2≤x≤4}．.......3分 ∴A∪B={x|-2≤x≤5}．. ..................5分 （2）∵B⊆A，∴，解得m≥3， .................9分 ∴m的取值范围为{m|m≥3} .................10分 ‎18. 解：（1） ．.................1分 ‎ ‎ .................2分 ‎ .................3分 ‎ .................4分 当时，满足；当，满足..........5分 ‎ .................6分 ‎（2）由已知得 .................7分 ‎① 若时，，得，此时………8分 ‎② 若为单元素集时，，，当时，；…9分 ‎③ 若为二元素集时，则，，此时无解。..11分 综上所述：实数的取值范围是………………12分 ‎19. 解 (1)函数的定义域为R,‎ 因为函数是奇函数.‎ 所以，所以. .................2分 经检验得，符合题意。（用定义求的不需要检验） ………………4分 ‎(2)函数在上为单调减函数, ……………………5分 证明如下: ，设，且，…………6分 ‎ ……………………………..10分 ‎，即 所以函数在上为单调减函数。…………………….12分 ‎20、解：（1）当x＜0时，-x＞0，因为f（x）是偶函数，所以f（-x）=f（x）．……（2分） 所以f（x）=f（-x）=x2+2x． ………………………（3分） 综上：f（x）= ……………………………（4分）． （2）图象如图所示． 单调增区间：[-1，0]，[1，+∞） 单调减区间：（-，-1）,(0,1) …………………………（8分）． （3）当x＞0时，x2-2x=1 解得 因为x＞0，所以 当x＜0时，x2+2x=1，解得x=-1-或，‎ 因为x＜0，所以x=-1- 综上所述，…………………………………（12分）‎ ‎21.解:（1），‎ 设，‎ ‎ …………………3分 ‎（2）函数，其对称轴方程是 ‎ ‎∵函数在区间上是单调函数， ∴ ，‎ ‎ ∴或，∴实数的取值范围是…………………6分 （3）令 则………………8分 当单调递减；当，单调递增；…………………9分 ‎，…………………………V10分 又，所以……………………11分 当时，函数的值域是………………….12分 ‎22.解：解：（Ⅰ）令x=y=0，得f（0+0）=f（0）+f（0），所以f（0）=0． 由f（1）=1，得f（2）=f（1）+f（1）=1+1=2， f（3）=f（2）+f（1）=2+1=3．…（2分） （Ⅱ）f（x）在R上是增函数，证明如下： 任取x1，x2∈R，且x1＜x2，则x2-x1＞0，且f（x2-x1）＞0， 所以f（x2）-f（x1）=f（x2-x1+x1）-f（x1） =f（x2-x1）+f（x1）-f（x1）=f（x2-x1）＞0， 即f（x1）＜f（x2），所以f（x）在R上是增函数．…（6分） （Ⅲ）由f（4x-a）+f（6+2x+1）＞2对任意 x∈R恒成立， 得f（4x-a+6+2x+1）＞f（2）恒成立． 因为f（x）在R上是增函数，所以4x-a+6+2x+1＞2恒成立， 即4x+2•2x+4＞a恒成立…（8分） 令g（x）=4x+2•2x+4=（2x+1）2+3， 因为2x＞0，所以g（x）＞4…（10分） 故a≤4…（12分）‎