【数学】2019届一轮复习人教A版立体几何学案(1) 16页

‎5.立体几何 ‎■要点重温…………………………………………………………………………·‎ ‎1．几何体的三视图排列规则：俯视图放在正视图下面，侧视图放在正视图右面，“长对正，高平齐，宽相等．”‎ 由几何体的三视图确定几何体时，要注意以下几点：‎ ‎(1)还原后的几何体一般为较熟悉的柱、锥、台、球的组合体．‎ ‎(2)注意图中实、虚线，实际是原几何体中的可视线与被遮挡线．‎ ‎(3)想象原形，并画出草图后进行三视图还原，把握三视图和几何体之间的关系，与所给三视图比较，通过调整准确画出原几何体．‎ ‎[应用1]　“牟合方盖”是我国古代数 家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合(牟合)在一起的方形伞(方盖)．其直观图如图11，图中四边形是为体现其直观性所作的辅助线．当其主视图和侧视图完全相同时，它的俯视图可能是(　　)‎ ‎ 图11‎ ‎[解析]　俯视图是正方形，曲线在其上面的投影恰为正方形的对角线，故选B.‎ ‎[答案]　B ‎2．空间几何体表面积和体积的求法 几何体的表面积是各个面的面积之和，组合体的表面积应注意重合部分的处理，求几何体的体积常用公式法、割补法、等积变换法．‎ ‎[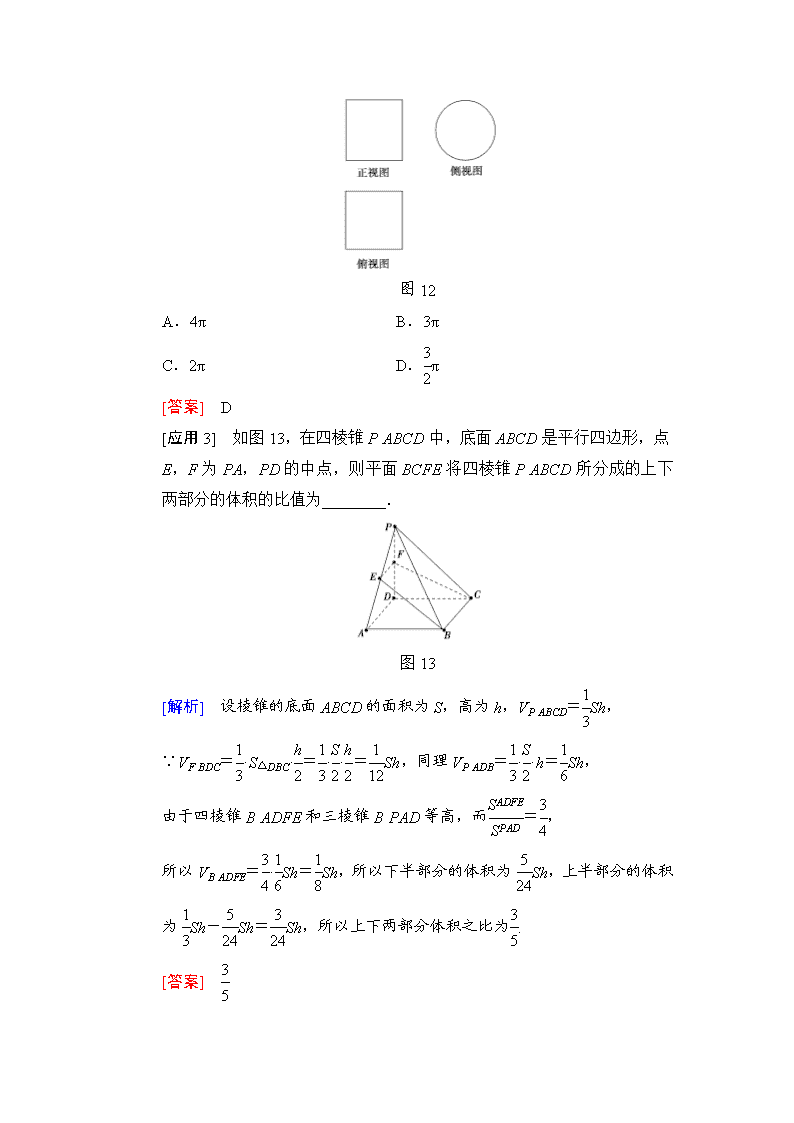应用2]　如图12所示，一个空间几何体的正视图和俯视图都是边长为1的正方形，侧视图是一个直径为1的圆，那么这个几何体的表面积为(　　)‎ ‎【导 号：07804184】‎ 图12‎ A．4π　　　 B．3π C．2π D．π ‎[答案]　D ‎[应用3]　如图13，在四棱锥PABCD中，底面ABCD是平行四边形，点E，F为PA，PD的中点，则平面BCFE将四棱锥PABCD所分成的上下两部分的体积的比值为________．‎ 图13‎ ‎[解析]　设棱锥的底面ABCD的面积为S，高为h，VPABCD＝Sh，‎ ‎∵VFBDC＝·S△DBC·＝··＝Sh，同理VPADB＝··h＝Sh，‎ 由于四棱锥BADFE和三棱锥BPAD等高，而＝，‎ 所以VBADFE＝·Sh＝Sh，所以下半部分的体积为Sh，上半部分的体积为Sh－Sh＝Sh，所以上下两部分体积之比为.‎ ‎[答案]　 ‎3．多面体与球接、切问题的求解策略 ‎(1)涉及球与棱柱、棱锥的接、切问题时，一般过球心及多面体中的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题，再利用平面几何知识寻找几何体中元素间的关系，或只画内接、外切的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解．‎ ‎(2)若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两互相垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，则4R2＝a2＋b2＋c2求解．‎ ‎[应用4]　一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积是，那么这个三棱柱的体积是(　　)‎ A．96 B．16 C．24 D．48 ‎[解析]　如图，设球的半径为R，由πR3＝，得R＝2.‎ 所以正三棱柱的高h＝4.‎ 设其底面边长为a，则·a＝2，‎ 所以a＝4，‎ 所以V＝×(4)2×4＝48.‎ ‎[答案]　D ‎[应用5]　已知三棱锥ABCD内接于球O，且BC＝BD＝CD＝2，若三棱锥ABCD体积的最大值为4，则球O的表面积为(　　) ‎ ‎【导 号：07804185】‎ A．16π B．25π C．36π D．64π ‎[解析]　如图，当三棱锥的体积最大值为4，即××(2)2××h＝4，解得h＝4，点A在如图所示的位置时，三棱锥的体积最大，即AO′＝4，并且在如图所示的三角形中，OA＝OC＝R，OO′＝4－R，O′C＝2×＝2，所以在直角三角形OO′C中，R2＝(4－R)2＋22，解得R＝，球的表面积为S＝4πR2＝25π，故选B.‎ ‎[答案]　B ‎4．空间平行问题的转化关系 平行问题的核心是线线平行，证明线线平行的常用方法有：三角形的中位线、平行线分线段成比例(三角形相似)、平行四边形等．‎ ‎[应用6]　下列命题正确的序号是________．‎ ‎(1)如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面．‎ ‎(2)如果直线a和平面α满足a∥α，那么a与α内的任何直线平行．‎ ‎(3)如果直线a，b和平面α满足a∥α，b∥α，那么a∥b.‎ ‎(4)如果直线a，b和平面α满足a∥b，a∥α，b⊄α，那么b∥α.‎ ‎[答案]　(4)‎ ‎5．空间垂直问题的转化关系 垂直问题的核心是线线垂直，证明线线垂直的常用方法有：等腰三角形底边上的中线、勾股定理、平面几何方法等．‎ ‎[应用7]　已知两个平面垂直，下列命题 ‎①一个平面内已知直线必垂直于另一个平面内的任意一条直线；‎ ‎②一个平面内的已知直线必垂直于另一个平面的无数条直线；‎ ‎③一个平面内的任一条直线必垂直于另一个平面；‎ ‎④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面．‎ 其中正确命题的个数是(　　)‎ A．3 B．2‎ C．1 D．0‎ ‎[答案]　B ‎6．平面图形的翻折，立体图形的展开等一类问题，要注意翻折，展开前后有关几何元素的“不变量”与“不变性”．‎ ‎[应用8]　(1)如图14(1)，在Rt△ABC中，∠ABC＝90°，∠BAC＝60°，AB＝2，D、E分别为AC、BD的中点，连接AE并延长交BC于F，将△ABD沿BD折起，使平面ABD⊥平面BCD，如图14(2)所示．‎ 图14(1)　　　　　　　图14(2)‎ ‎(1)求证：AE⊥平面BCD；‎ ‎(2)求平面AEF与平面ADC所成的锐二面角的余弦值；‎ ‎(3)在线段AF上是否存在点M使得EM∥平面ADC？若存在，请指出点M的位置；若不存在，说明理由．‎ ‎[解]　(1)证明：在Rt△ABC中，∠ABC＝90°，D为AC的中点，∴AD＝BD＝DC，‎ 又∠BAC＝60°，所以三角形ABD为等边三角形；‎ 又E为BD的中点，∴AE⊥BD.‎ 因为平面ABD⊥平面BCD，交线为BD，AE⊂平面ABD，所以AE⊥平面BCD.‎ ‎(2)由AE⊥平面BCD可知．AE⊥EF.由题意知EF⊥BD，AE⊥BD，故以E为坐标原点，分别以EF、ED、EA所在直线为x轴，y轴，z轴，建立空间直角坐标系Exyz.‎ 由(1)得，AB＝BD＝DC＝AD＝2，BE＝ED＝1，‎ 计算得AE＝，BC＝2，BF＝，‎ 则E(0,0,0)，D(0,1,0)，B(0，－1,0)，A(0,0，)，‎ F，C(，2,0)，‎ 则＝(，1,0)，＝(0,1，－)，‎ 易知平面AEF的一个法向量为＝(0,1,0)．‎ 设平面ADC的法向量为n＝(x，y，z)，则 ，即，‎ 令z＝1，得y＝，x＝－1，∴n＝(－1，，1)．‎ cos〈n，〉＝＝.‎ 所以平面AEF与平面ADC所成的锐二面角的余弦值为 ‎(3)设＝λ，其中λ∈[0,1]，‎ ‎∵＝，∴＝λ＝λ，其中λ∈[0,1]，‎ ＝＋＝，由·n＝0，解得λ＝∈(0,1)．‎ 所以在线段AF上存在点M，使EM∥平面ADC，且AM∶AF＝3∶4.‎ ‎7. “转化法”求空间角 ‎(1)设两条异面直线a，b所成的角为θ，两条直线的方向向量分别为a，b.‎ 因为θ∈，故有cos θ＝|cos〈a，b〉|＝||.‎ ‎(2)设直线l和平面α所成的角为θ，l是斜线l的方向向量，n是平面α的法向量，则sin θ＝|cos〈l，n〉|＝||.‎ ‎(3)设二面角αlβ的大小为θ，n1，n2是二面角αlβ的两个半平面的法向量，则|cos θ|＝|cos〈n1，n2〉|，两个角之间的关系需要根据二面角的取值范围 确定．‎ ‎[应用9]　在三棱锥PABC中，AB⊥BC，AB＝BC＝PA，点O，D分别是AC，PC的中点，OP⊥底面ABC，求直线PA与平面PBC所成角的正弦值．‎ ‎[解]　∵OP⊥平面ABC，OA＝OC，AB＝BC，‎ ‎∴OA⊥OB，OA⊥OP，OB⊥OP.‎ 以O为原点，射线OP为z轴正方向，OA为x轴正方向，OB为y轴正方向，建立空间直角坐标系Oxyz(如图)．‎ 设AB＝a，‎ 则A，B，C，‎ 设OP＝h，则P(0,0，h)，由PA＝AB，则PA＝2a，‎ 则P＝，＝.‎ 可求得平面PBC的一个法向量为n＝，‎ ‎∴cos〈，n〉＝＝，‎ 设PA与平面PBC所成的角为θ，‎ 则sin θ＝|cos〈，n〉|＝.‎ ‎8．求点到平面的距离的方法 ‎(1)“等积法”：求解点到面的距离常转化为锥体的高，利用三棱锥体积公式求点到平面的距离．‎ ‎(2)“向量法”：如图，设P在平面α外，n为平面α的法向量，在平面α内任取一点Q，则点P到平面α的距离d＝.‎ 图15‎ ‎[应用10]　正方体ABCDA1B1C1D1的棱长为1，O是底面A1B1C1D1的中心，则点O到平面ABC1D1的距离为________. ‎ ‎【导 号：07804186】‎ ‎[解析]　建立如图所示的空间直角坐标系，‎ 则A(1,0,0)，B(1,1,0)，D1(0,0,1)，C1(0,1,1)，O.‎ 设平面ABC1D1的法向量为 n＝(x，y，z)，‎ 则∴令z＝1，得 ‎∴n＝(1,0,1)，又＝，‎ ‎∴O到平面ABC1D1的距离d＝＝＝.‎ ‎[答案]　 ‎■查缺补漏…………………………………………………………………………·‎ ‎1．已知m，n为空间中两条不同的直线，α，β为空间中两个不同的平面，下列命题中正确的是(　　)‎ A．若m∥α，m∥β，则α∥β B．若m⊥α，m⊥n，则n∥α C．若m∥α，m∥n，则n∥α D．若m⊥α，m∥β，则α⊥β D　[对于选项A，若m∥α，m∥β，则可能α，β相交，或者α∥β，所以选项A不正确；对于选项B，若m⊥α，m⊥n，则可能n⊂α，或n∥α，所以选项B不正确；对于选项C，若m∥α，m∥n，则n⊂α，或n∥α，所以选项C不正确；对于选项D，若m⊥α，m∥β，则由线面平行可得在平面β内存在一条直线l，使得m∥l，然后由m⊥α可得l⊥α，进而得出α⊥β，故选D.]‎ ‎2. 一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是，(1,1,0)，，(1,0,1)，画该四面体三视图中的正视图时，以yOz平面为投影面，则得到的正视图可以为(　　)‎ A　[由图可得，故选A. ‎ ‎]‎ ‎3．如图16，在正方体ABCDA1B1C1D1中，M，N，P，Q分别是AA1，A1D1，CC1，BC的中点，给出以下四个结论：①A1C⊥MN；②A1C∥平面MNPQ；③A1C与PM相交；④NC与PM异面．其中不正确的结论是(　　)‎ 图16‎ A．① B．② C．③ D．④‎ B　[作出过M，N，P，Q四点的截面交C1D1于点S，交AB于点R，如图中的六边形MNSPQR，显然点A1，C分别位于这个平面的两侧，故A1C与平面MNPQ一定相交，不可能平行，故结论②不正确．]‎ ‎4．如图17， 格纸上小正方形的边长为1，粗线或虚线画出某几何体的三视图，该几何体的体积为(　　)‎ ‎【导 号：07804187】‎ 图17‎ A．8 B．12‎ C．18 D．24‎ B　[由题意得，根据给定的三视图可知，该几何体为如图所示的几何体，是一个三棱锥与三棱柱的组合体，其中三棱锥的体积为V1＝××4×3×2＝4，三棱柱的体积为V2＝2V1＝2×4＝8，所以该几何体的体积为V＝12，故选B.]‎ ‎5.如图18，已知六棱锥PABCDEF的底面是正六边形，PA⊥平面ABC，PA＝2AB，则下列结论正确的是(　　)‎ 图18‎ A．PB⊥AD B．平面PAB⊥平面PBC C．直线BC∥平面PAE D．直线PD与平面ABC所成的角为45°‎ D　[若PB⊥AD，则AD⊥AB，但AD与AB成60°角，A错误；平面PAB与平面ABD垂直，所以平面PAB一定不与平面PBC垂直，B错误；BC与AE是相交直线，所以BC一定不与平面PAE平行，C错误；直线PD与平面ABC所成角为∠PDA，在Rt△PAD中，AD＝PA，所以∠PDA＝45°，D正确．]‎ ‎6．设三棱柱ABCA1B1C1的侧棱与底面垂直，∠BCA＝90°，BC＝CA＝2，若该棱柱的所有顶点都在体积为的球面上，则直线B1C与直线AC1所成角的余弦值为(　　)‎ A．－ B． C．－ D． B　[由已知，若棱柱的所有顶点都在球面上，则同高的长方体8个顶点也在球面上，且外接球的直径为长方体的体对角线，由球体体积可得直径为4，由于长方体底面为边长为2的正方形，故侧面的对角线为2，由余弦定理可知，直线B1C与直线AC1所成角的余弦值为＝.]‎ ‎7．三棱锥PABC中，AB＝BC＝，AC＝6，PC⊥平面ABC，PC＝2，则该三棱锥外接球的表面积为(　　)‎ A.π B．π C.π D．π D　[由题意可知，△ABC中AC边上的高为＝，球心O在底面ABC的投影即为△ABC的外心D，设DA＝DB＝DC＝x，∴x2＝32＋2，解得x＝，∴R2＝x2＋＝＋1＝(其中R为三棱锥外接球的半径)，∴外接球的表面积S＝4πR2＝π，故选D.]‎ ‎8．在梯形ABCD中，∠ABC＝，AD∥BC，BC＝2AD＝2AB＝2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为________. ‎ ‎【导 号：07804188】‎ 　[过点C作CE垂直AD所在直线于点E，梯形ABCD绕AD所在直线旋转一周而形成的旋转体是由以线段AB的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE的长为底面圆半径，ED为高的圆锥，如图所示，该几何体的体积为V＝V圆柱－V圆锥＝π·AB2·BC－·π·CE2·DE＝π×12×2－×12×1＝.]‎ ‎9．如图19，在直三棱柱ABCA1B1C1中，AB＝1，BC＝2，AC＝，AA1＝3，M为线段BB1上的一动点，则过A，M，C1三点的平面截该三棱柱所得截面的最小周长为________．‎ 图19‎ ‎3＋　[由图形可知，当AM＋MC1最小时，所得截面的周长最小，如图所示把平面A1ABB1与平面C1CBB1展开成一个平面AA1C1C，则AM＋MC1最短为AC1＝＝3，所以截面的最小周长为3＋＝3＋.]‎ ‎10．在封闭的直三棱柱ABCA1B1C1内有一个体积为V的球，若AB⊥BC，AB＝6，BC＝8，AA1＝5，则V的最大值是________．‎ π　[由题意得要使球的体积最大，则球与直三棱柱的若干面相切，设球的半径为R，∵△ABC的内切圆半径为＝2，∴△ABC的内切球半径为2，∴R≤2，又2R≤5，‎ 即R≤，∴取交集R≤2，∴Vmax＝π×23＝π.]‎ ‎11．如图20，四棱锥PABCD中，∠ABC＝∠BAD＝90°，BC＝2AD，△PAB与△PAD都是等边三角形．‎ 图20‎ ‎(1)证明：PB⊥CD；‎ ‎(2)求二面角APDB的余弦值．‎ ‎[解]　(1)证明：如图，取BC的中点E，连接DE，则ADEB为正方形，过P作PO⊥平面ABCD，垂足为O，‎ 连接OA，OB，OE，OD，则由△PAB和△PAD都是等边三角形可知PA＝PB＝PD，∴OA＝OB＝OD，‎ 即点O为正方形ADEB对角线的交点，‎ 故OE⊥BD，从而OE⊥平面PBD，‎ ‎∴OE⊥PB，∵O是BD的中点，E是BC的中点，‎ ‎∴OE∥CD，因此PB⊥CD.‎ ‎(2)由(1)可知，OE，OB，OP两两垂直，‎ 以O为原点，OE方向为x轴正方向，OB方向为y轴正方向，OP方向为z轴正方向，建立如图所示的空间直角坐标系Oxyz，设AB＝2，则A(－，0,0)，D(0，－，0)，P(0,0，)，‎ ＝(，－，0)，＝(，0，)，‎ 设平面PAD的法向量n＝(x，y，z)，‎ n·＝x－y＝0，n·＝x＋z＝0，‎ 取x＝1，得y＝1，z＝－1，得n＝(1,1，－1)，‎ ‎∵OE⊥平面PBD，设平面PBD的法向量为m，取m＝(1,0,0)，‎ 由图象可知二面角APDB的大小为锐角，‎ ‎∴二面角APDB的余弦值为 cos θ＝＝＝.‎ ‎12．已知三棱柱ABCA1B1C1，侧面BCC1B1⊥底面ABC.‎ 图21‎ ‎(1)若M，N分别是AB，A1C的中点，求证：MN∥平面BCC1B1.‎ ‎(2)若三棱柱ABC－A1B1C1的各棱长均为2，侧棱BB1与底面ABC所成的角为60°.问：在线段A1C1上是否存在一点P，使得平面B1CP⊥平面ACC1A1？若存在，求C1P与PA1的比值；若不存在，说明理由．‎ ‎[解]　(1)证明：连接AC1，BC1，则AN＝NC1，‎ ‎∵AM＝MB，‎ ‎∴MN∥BC1.‎ 又∵BC1⊂平面BCC1B1，‎ ‎∴MN∥平面BCC1B1.‎ ‎(2)作B1O⊥BC于O，‎ ‎∵面BCC1B1⊥底面ABC，∴B1O⊥面ABC.‎ 以O为原点，建立如上图所示的空间直角坐标系，则A(0，，0)，B(－1,0,0)，C(1,0,0)B1(0,0，)．‎ 由＝＝可求出A1(1，，)，C1(2,0，)．‎ 设P(x，y，z)，＝λ，‎ 解得P，‎ 则＝，＝(－1,0，)．‎ 设平面B1CP的法向量为n1＝(x，y，z)，‎ 由 解得n1＝.‎ 同理可求出平面ACC1A1的法向量n2＝(，1，－1)．‎ 由面B1CP⊥平面ACC1A1，得n1·n2＝0，即3＋－1＝0解得，λ＝3，所以A1C1＝3A1P，从而C1P∶PA1＝2.‎